Перпендикулярность прямых в пространстве

ЗАДАНИЕ
1. Записать определение перпендикуярности прямых
2. Записать теорему без доказательства
( с чертежём)
3. Решить задачу, образец решения показан

Вопросы для повторения: (УСТНО)
1. Перечислите случаи расположения прямых в пространстве.
2. Дайте определение пересекающихся, параллельных, скрещивающихся прямых.
3. Перечислите случаи расположения прямой и плоскости в пространстве.
4. Дайте определение пересекающихся, параллельных прямой и плоскости.
5. Перечислите случаи расположения плоскостей в пространстве.
6. Дайте определение пересекающихся, параллельных плоскостей.

Определение:
Прямые называются перпендикулярными, если они пересекаются под прямым углом

Теорема:
Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны

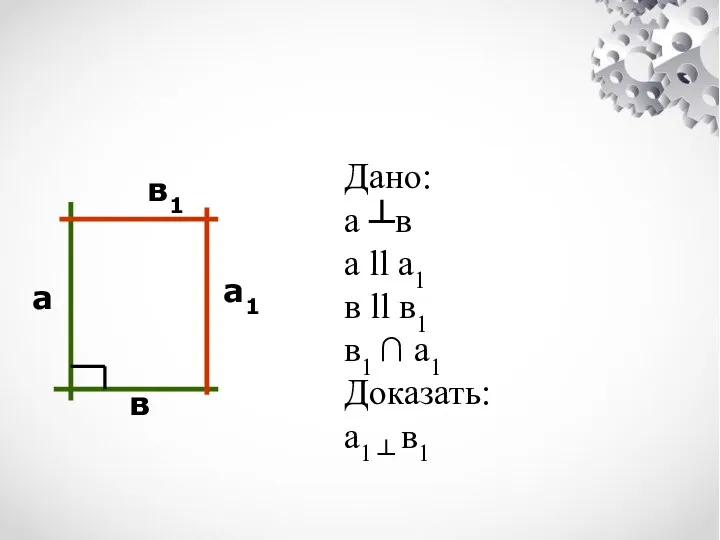
а
в
в1
а1
Дано:
а ┴в
а ll а1
в ll в1
в1 ∩ а1
Доказать:
а1 ┴ в1

Доказательство:
1. в ll в1, а ┴ в, следовательно
а ┴ в1 2. а ll а1, а ┴ в1, следовательно а1┴ в1
Ч.т.д

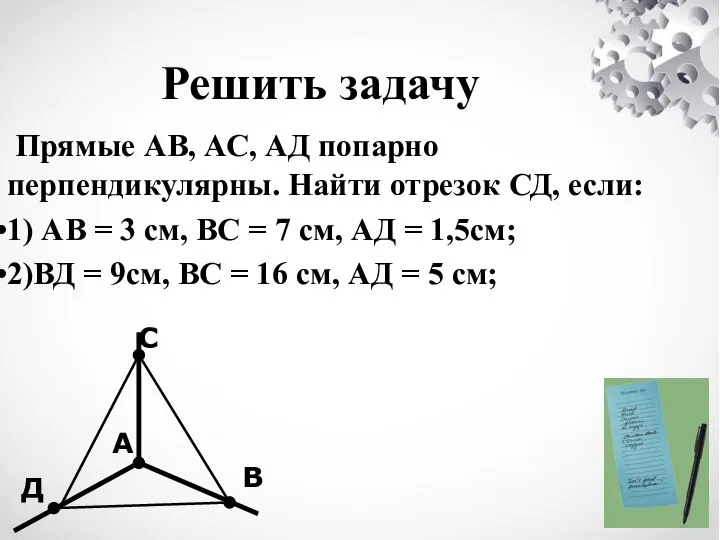
Решить задачу
Прямые АВ, АС, АД попарно перпендикулярны. Найти отрезок СД, если:
1) АВ = 3 см, ВС = 7 см, АД = 1,5см;
2)ВД = 9см, ВС = 16 см, АД = 5 см;
Д
А
С
В

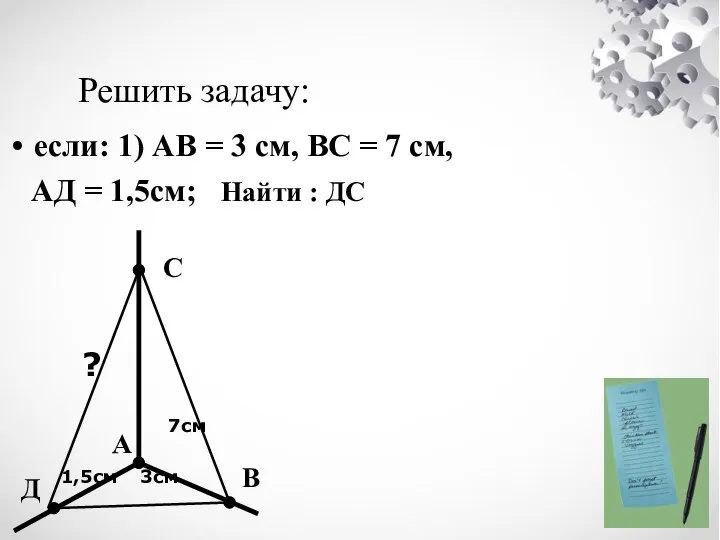
Решить задачу:
если: 1) АВ = 3 см, ВС = 7 см, АД = 1,5см; Найти : ДС
Д
А
С
В
1,5см
7см
3см
?

При решении задачи исполь зуется теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
с2 = а2 + в2

РЕШЕНИЕ ЗАДАЧИ
∆САВ- прямоуг. СВ2 = СА2 + АВ2
72 = СА2 + 32
СА2 = 72 - 32
СА2 = 40
∆САД- прямоуг. ДС2 = ДА2 + СА2
ДС2 = 1,52 + 40
ДС2 = 42, 25
ДС = √42, 25 ≈ 6,5 (см)