Pervoobraznaya

1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
Под дифференцированием функции f (х) мы понимаем нахождение ее производной f ′(х).
Нахождение функции f (х) по заданной ее производной f ′(х) называют операцией интегрирования.

Таким образом, операция интегрирования обратна операции дифференцирования. Следовательно, операция интегрирования состоит в том, что по заданной производной
f ′(х) находят (восстанавливают) функцию f (х).

Определение: Функция F(х) называется первообразной для функции f (х) на некотором промежутке, если для всех х из этого промежутка F ′(х)=f(x).
Например, функция F(x)=x2 есть первообразная для функции f(x)=2x на промежутке (-∞,+∞), так как для всех действительных х справедливо равенство F ′(х)=(х2)′=2х
Множество всех первообразных для функции f(x) можно представить в виде F(x)+С, где С – любое действительное число.

f (х) находится неоднозначно, ведь в качестве f (х) могут быть использованы и такие функции, как
f (х) = х4 + 3,
f (х)= х4 — 6,
и др., так как производная каждой из данных функций равна 4х3. Все эти функции отличаются друг от друга только постоянным слагаемым.
Общее решение задачи можно записать в виде
f (х)= х4 +С, где С — произвольное действительное число. Любую из найденных функций f (х) называют первообразной для функции f '(х) = 4х3.

Упражнение с решением
1) Доказать, что функция F (х) есть первообразная для функции f (х) на заданном промежутке, если F (х)=3х4, f (х)=12х3, (-∞,+∞).
Решение. Так как F (x) = 3х4, то F ′(х)= (3х4)'= 12х3 = f(x) для всех х, что и требовалось доказать.
2)F(x)=sin x является первообразной функции
f(x)=cos x, так как (sin х)′=cos x

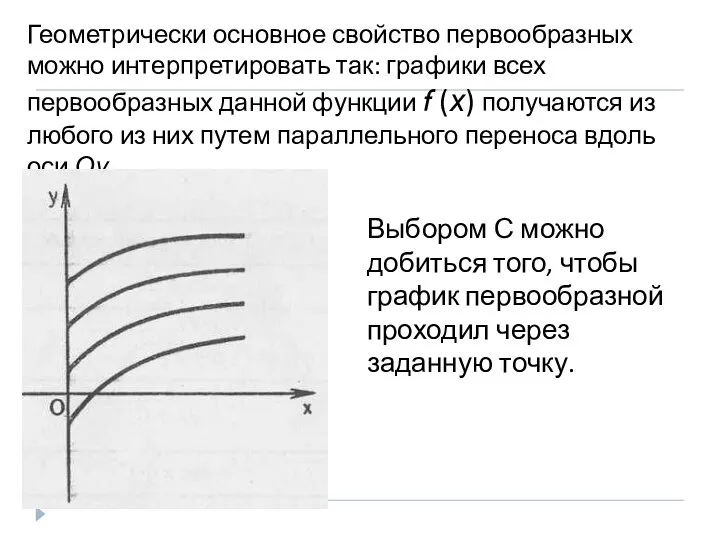
Геометрически основное свойство первообразных можно интерпретировать так: графики всех первообразных данной функции f (х) получаются из любого из них путем параллельного переноса вдоль оси Оу
Выбором С можно добиться того, чтобы график первообразной проходил через заданную точку.

Пример

упражнения с решениями

Таблица первообразных для некоторых функций:

3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
1. Если F(х) есть первообразная для f(х) ,
a G(х) — первообразная для g(х), то F(х) +G(х) есть первообразная для f(х) +g(х), т. е.
(F(х) + G(х) )' = f(х) + g(х).

2. Если F(х) есть первообразная для f(х), a k — постоянная, то kF(х) есть первообразная для kf(х),
т. е. (kF(х) )' = kf(х).

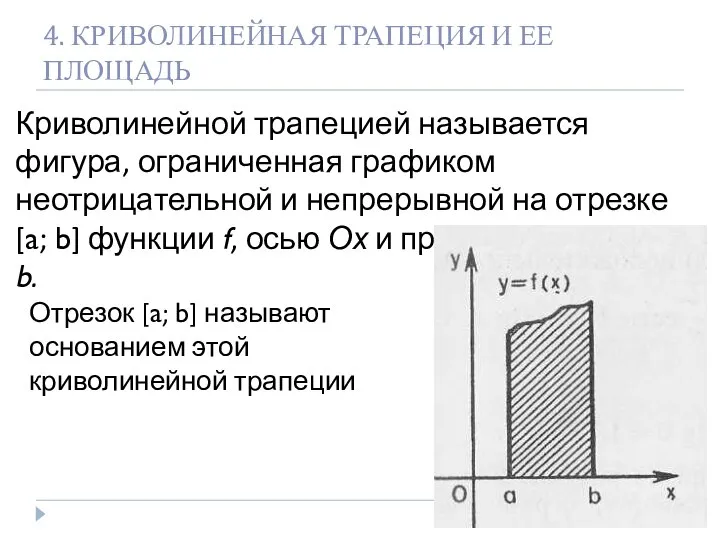
4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции f, осью Ох и прямыми х = а и х = b.
Отрезок [a; b] называют основанием этой криволинейной трапеции

Теорема. Пусть f(х) – непрерывная и неотрицательная на отрезке [a; b] функция, а S(х)–площадь соответствующей криволинейной трапеции . Если F есть первообразная для f па интервале, содержащем отрезок [a; b] , то
S = F(b)— F (а).

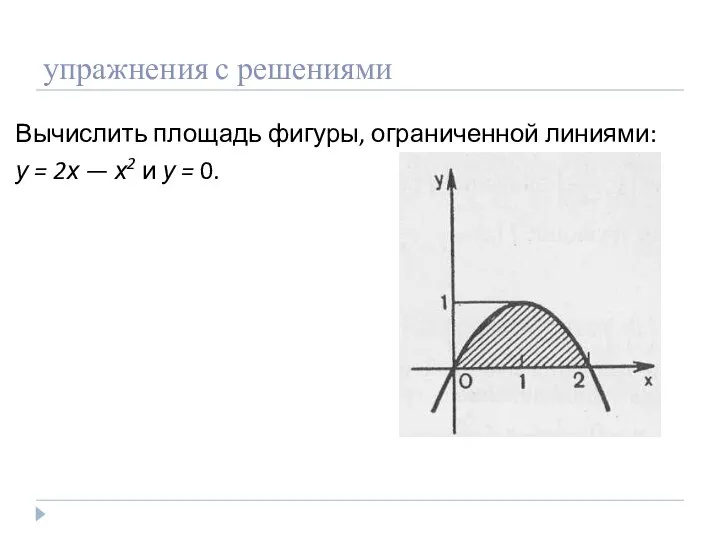
упражнения с решениями
Вычислить площадь фигуры, ограниченной линиями:
у = 2х — х2 и у = 0.