Статистическая радиотехника. Случайный процесс, ансамбль его реализаций

ПЛАН ЛЕКЦИИ 4
Случайный процесс, ансамбль его реализаций, сечение случайного процесса и сечение ансамбля реализаций
Характеристики распределений и моментные функции случайных процессов
Стационарные и эргодические случайные процессы
Спектральные характеристики стационарных случайных процессов, теорема Винера-Хинчина
Равенство Парсеваля

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайный процесс – это случайная функция времени z(t), значения которой в любой момент времени из области ее определения являются случайными величинами (априорно неизвестны)
Множество X(t) = {x1(t), x2(t),…, xn(t)} реализаций xi(t) случайного процесса z(t) называется ансамблем реализаций данного процесса

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайная величина z(t1), представленная мгновенными значениями случайного процесса z(t) в фиксированный момент времени t1, называется сечением случайного процесса
Множество X(t1) = {x1(t1), x2(t1),…, xn(t1)} мгновенных значений xi(t1) реализаций случайного процесса z(t) в фиксированный момент времени t1 называется сечением ансамбля реализации случайного процесса

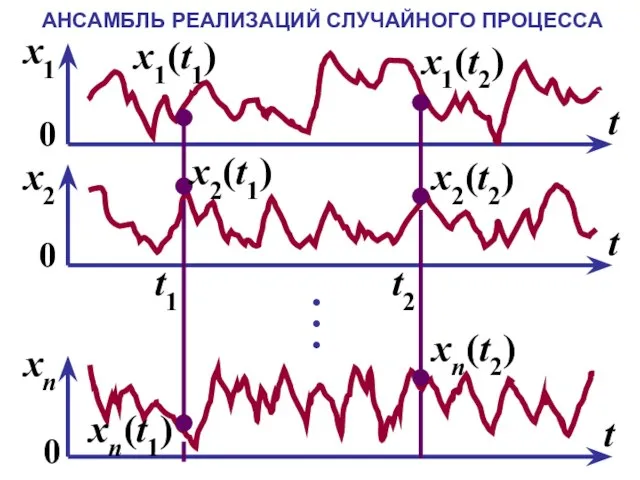
АНСАМБЛЬ РЕАЛИЗАЦИЙ СЛУЧАЙНОГО ПРОЦЕССА

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Одномерная функция распределения вероятностей F(x,t1) случайного процесса z(t) – функция распределения вероятностей сечения z(t1):

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Одномерная плотность вероятности p(x,t1) случайного процесса z(t) – плотность вероятности сечения z(t1):

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Двумерная функция распределения вероятностей F(x1,x2,t1,t2) случайного процесса z(t):

ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Двумерная плотность вероятности p(x,t1) случайного процесса z(t):
Многомерная плотность вероятности случайного процесса:

МОМЕНТНЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Математическое ожидание – первый момент сечения z(t), характеризует среднее значение случайного процесса в момент времени t :

МОМЕНТНЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Дисперсия – второй центральный момент сечения z(t), характеризует среднее значение квадрата флуктуаций случайного процесса в момент времени t :

МОМЕНТНЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции (функция автокорреляции, корреляционная функция, автокорреляционная функция) – второй центральный смешанный момент сечений z(t1) и z(t2), характеризует корреляцию или среднюю взаимную мощность флуктуаций случайного процесса в моменты времени t1 и t2

ФУНКЦИЯ КОРРЕЛЯЦИИ
При совмещении сечений z(t1) и z(t2)

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Случайный процесс называется стационарным в узком смысле, если его любые многомерные плотности вероятности инвариантны относительно временного сдвига τ:

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Любые моментные функции стационарных в узком смысле случайных процессов, определяемые по одному сечению, не зависят от времени:
Моментные функции, определяемые по двум сечениям, зависят только от разности временных аргументов

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Случайный процесс называется стационарным в широком смысле, если его, по крайней мере, одномерные и двумерные плотности вероятности инвариантны относительно временного сдвига τ
Моментные функции первого и второго порядка стационарного в широком смысле случайного процесса либо не зависят от времени, либо зависят только от разности временных аргументов

МОМЕНТНЫЕ ФУНКЦИИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции стационарного случайного процесса - четная

МОМЕНТНЫЕ ФУНКЦИИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции стационарного случайного процесса имеет максимум в нуле

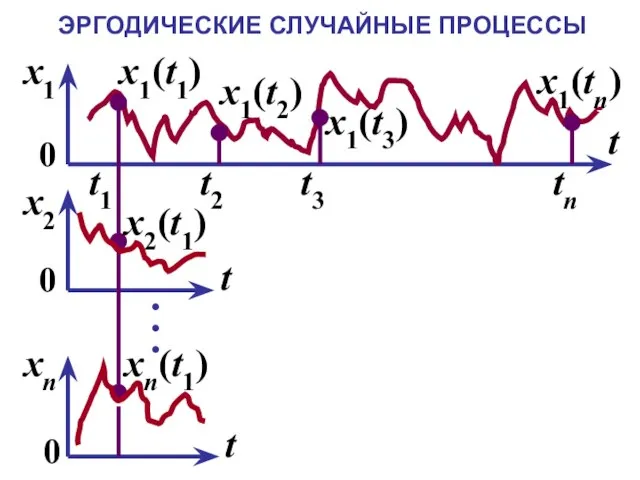
ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Стационарный случайный процесс называется эргодическим, если усреднение любой его вероятностной характеристики по ансамблю реализаций эквивалентно усреднению во времени по одной из реализаций
Условие эргодичности:

ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

МОМЕНТНЫЕ ФУНКЦИИ ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Дисперсия:
Математическое ожидание:

МОМЕНТНЫЕ ФУНКЦИИ ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции :
Значение функции корреляции характеризует корреляционную связь между двумя сечениями случайного процесса, разделенными временным промежутком длительностью τ

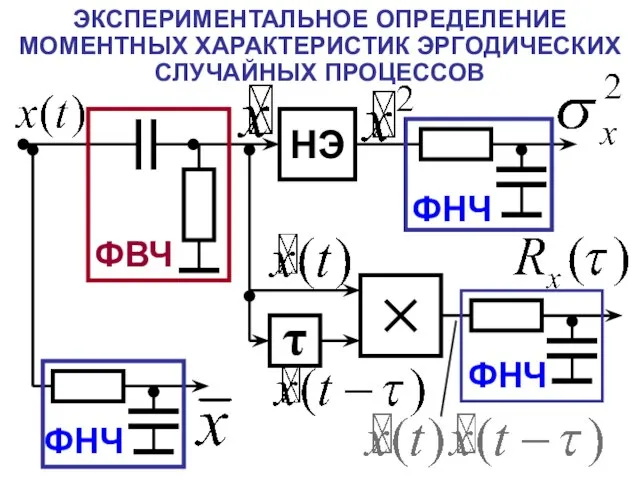
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТНЫХ ХАРАКТЕРИСТИК ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ

СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
S(ω) - спектральная плотность реализации x(t) стационарного случайного процесса z(t):

СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Математическое ожидание спектральной плотности как случайной функции частоты:
Математическое ожидание стационарного случайного процесса:

СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Спектральная плотность стационарного случайного процесса является случайной функцией частоты, математическое ожидание которой при любом значении частоты, кроме нулевого, равно нулю

ТЕОРЕМА ВИНЕРА-ХИНЧИНА
ST(ω) – спектральная плотность реализации x(t) случайного процесса на интервале длительностью T:

ТЕОРЕМА ВИНЕРА-ХИНЧИНА

ТЕОРЕМА ВИНЕРА-ХИНЧИНА

ТЕОРЕМА ВИНЕРА-ХИНЧИНА
Спектральная плотность мощности случайного процесса определяется математическим ожиданием суммарной мощности его спектральных составляющих на частотном интервале шириной в 1 Гц

ТЕОРЕМА ВИНЕРА-ХИНЧИНА

ТЕОРЕМА ВИНЕРА-ХИНЧИНА
Спектральная плотность мощности и функция корреляции стационарного случайного процесса связаны между собой парой преобразований Фурье

РАВЕНСТВО ПАРСЕВАЛЯ
Средняя мощность (дисперсия) стационарного случайного процесса равна сумме средних мощностей (дисперсий) всех спектральных составляющих данного процесса

СВОЙСТВА СПЕКТРА МОЩНОСТИ
Спектр мощности W(ω) - действительная, неотрицательная функция частоты, определенная на всей числовой прямой
Спектр мощности W(ω) – четная функция частоты: W(-ω) = W(ω)

ОДНОСТОРОННИЙ СПЕКТР МОЩНОСТИ

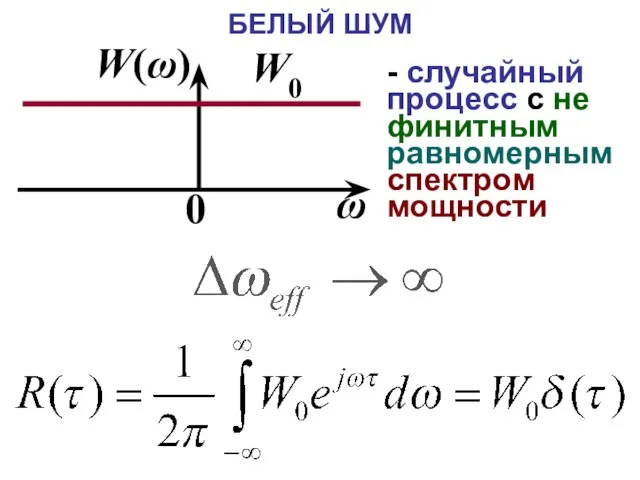
БЕЛЫЙ ШУМ
- случайный процесс с не финитным равномерным спектром мощности