Содержание
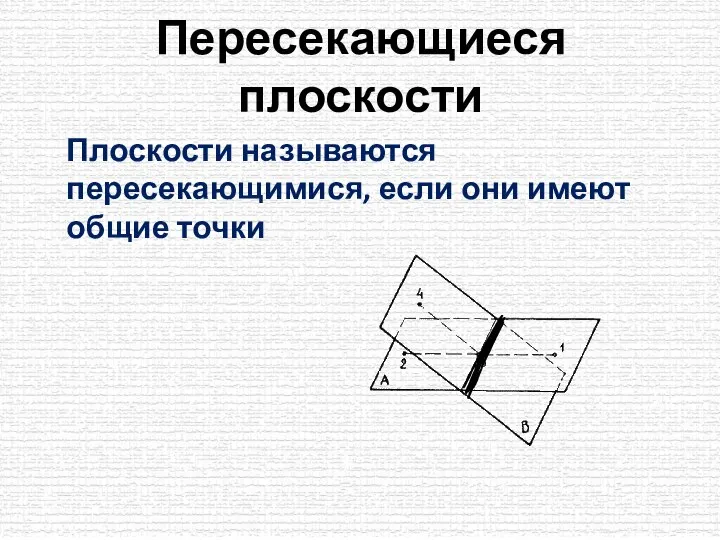
- 2. Пересекающиеся плоскости Плоскости называются пересекающимися, если они имеют общие точки
- 3. Параллельные плоскости Плоскости, не имеющие общих точек, называются параллельными
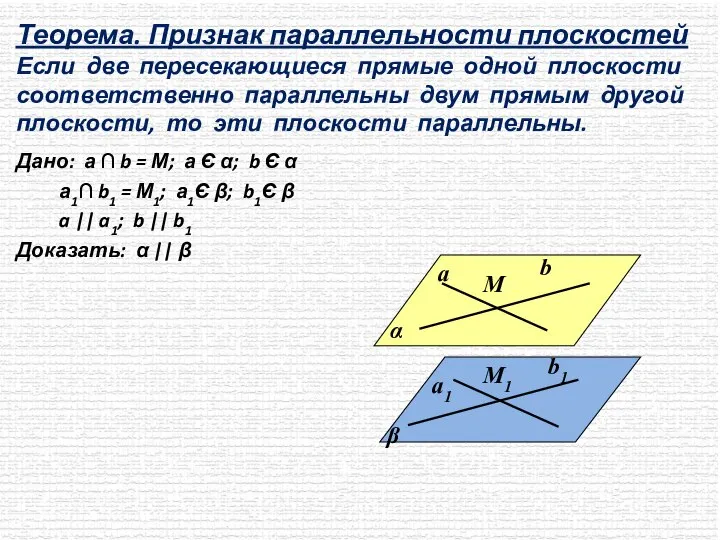
- 4. Теорема. Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости,
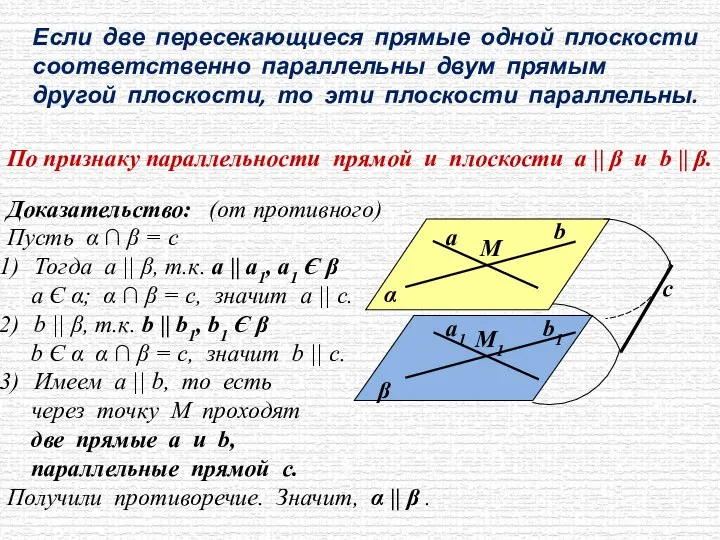
- 5. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
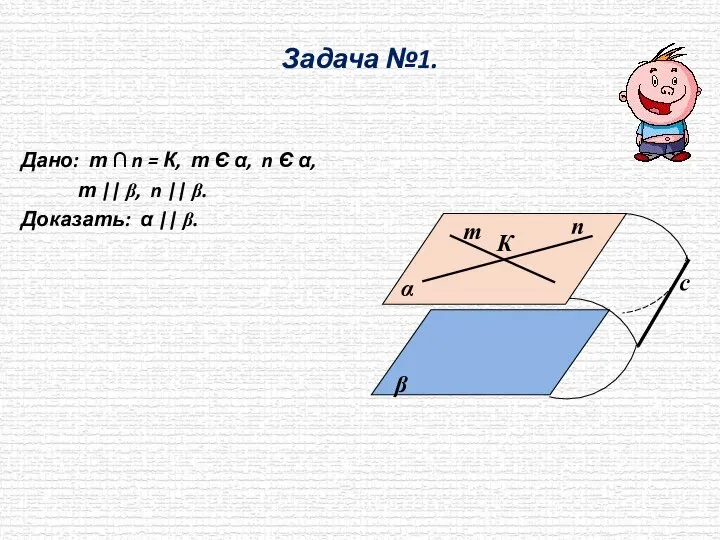
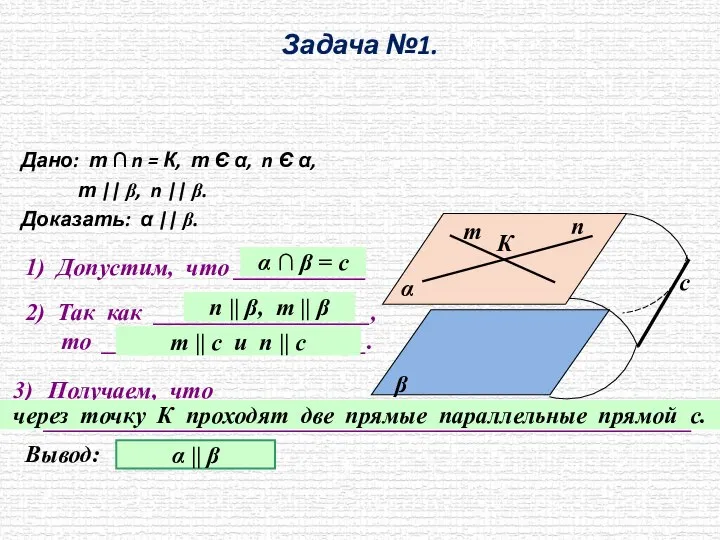
- 6. Задача №1. Дано: т ∩ n = К, т Є α, n Є α, т ||
- 7. Задача №1. Дано: т ∩ n = К, т Є α, n Є α, т ||
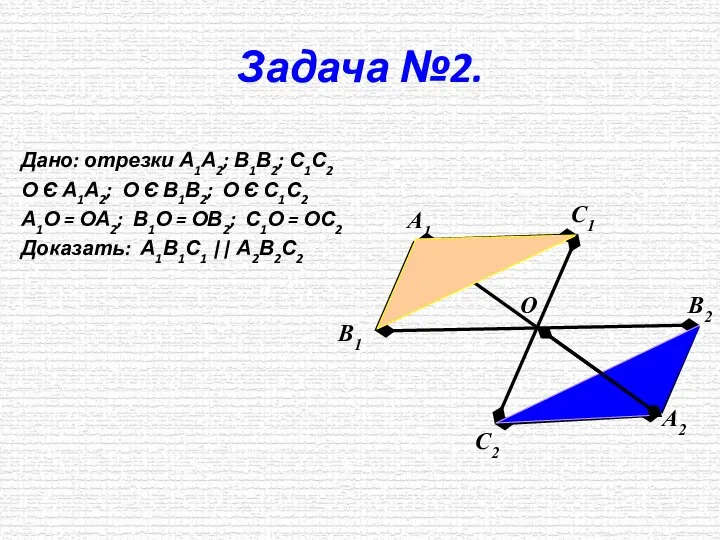
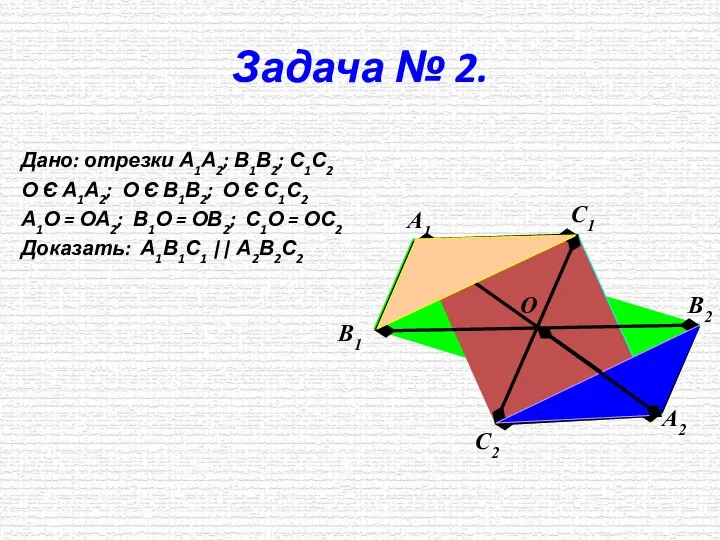
- 8. Задача №2. Дано: отрезки А1А2; В1В2; С1С2 О Є А1А2; О Є В1В2; О Є С1С2
- 9. Задача № 2. Дано: отрезки А1А2; В1В2; С1С2 О Є А1А2; О Є В1В2; О Є
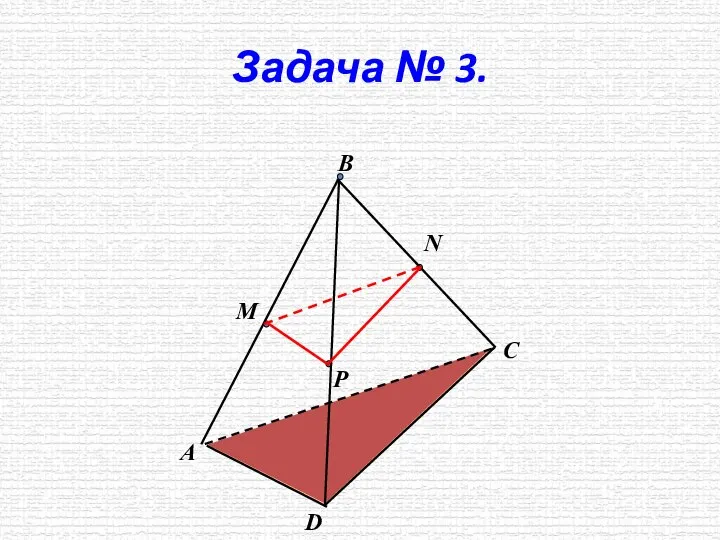
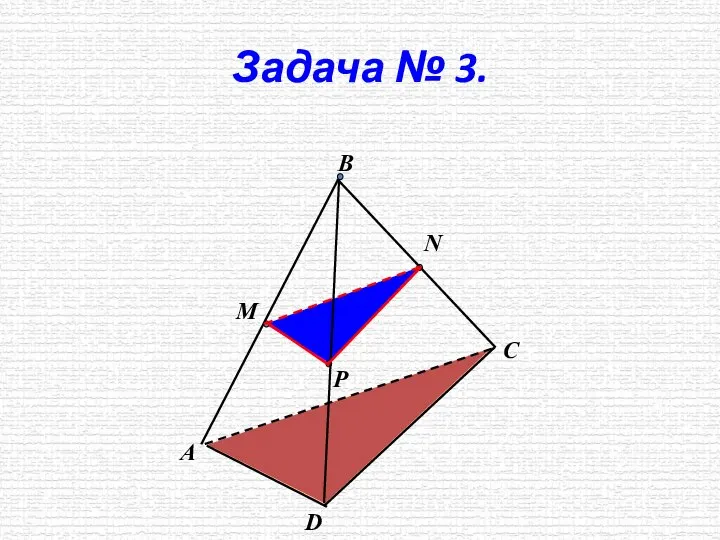
- 10. Задача № 3. М Р N А В D C
- 11. Задача № 3. М Р N А D C В
- 12. Проверка знаний Могут ли прямая и плоскость не иметь общих точек? Верно ли, что если две
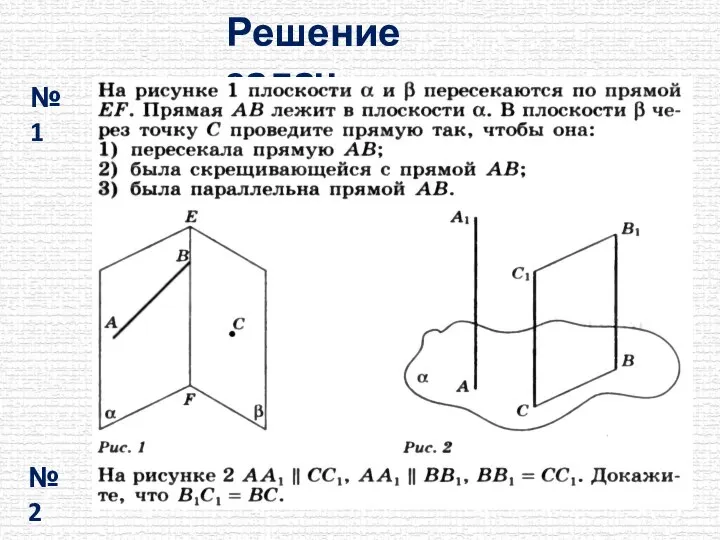
- 13. Решение задач № 1 № 2
- 14. № 3 № 4 Решение задач
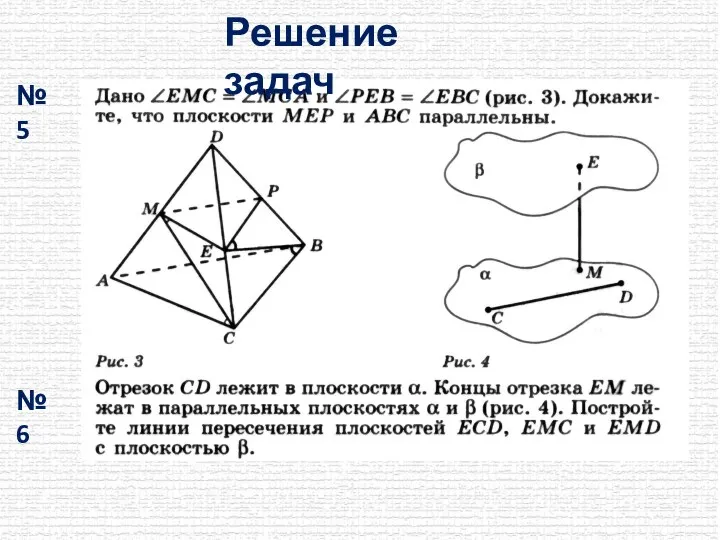
- 15. Решение задач № 5 № 6
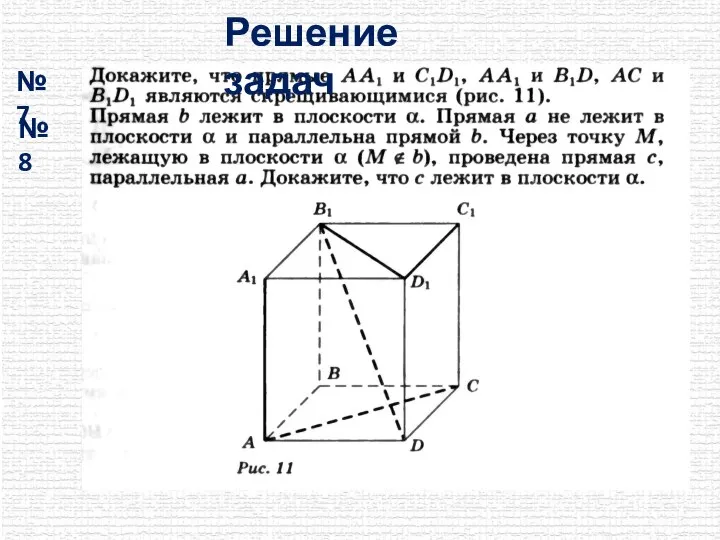
- 16. № 7 № 8 Решение задач
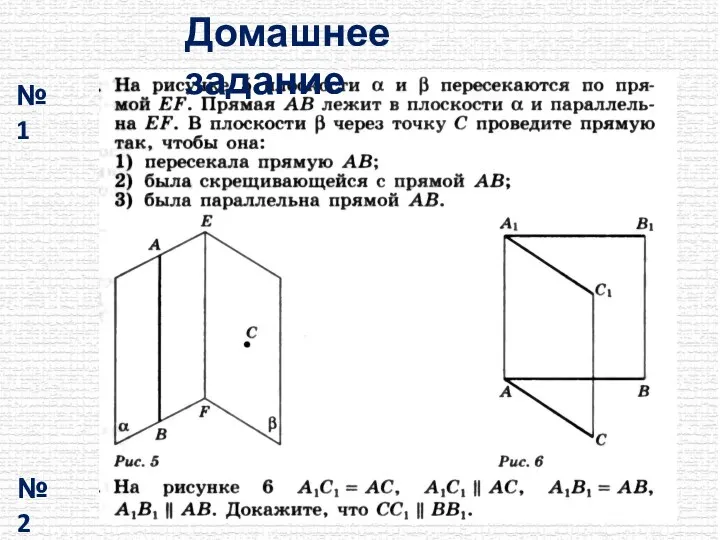
- 17. Домашнее задание № 1 № 2
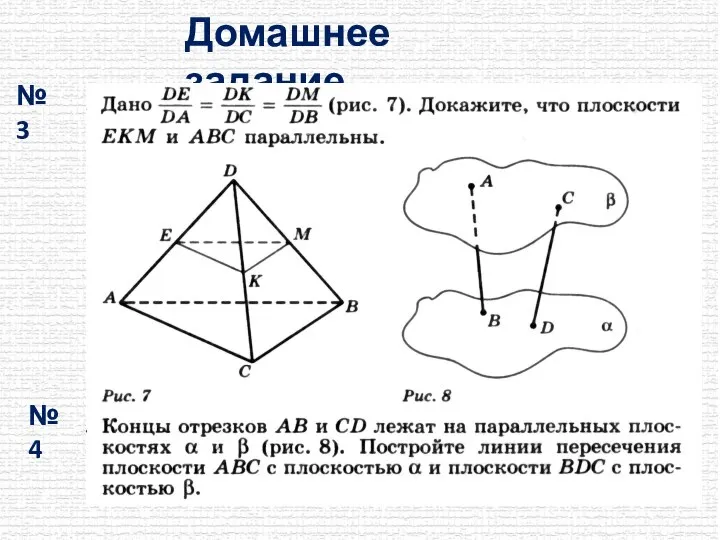
- 18. Домашнее задание № 3 № 4
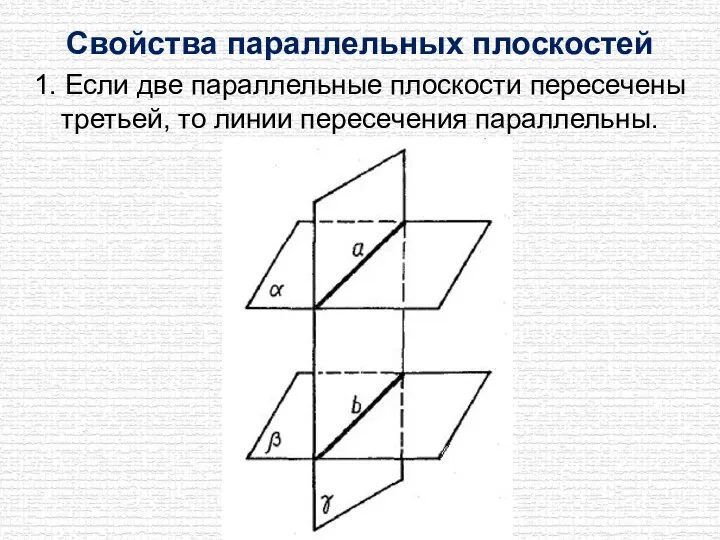
- 19. Свойства параллельных плоскостей 1. Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
- 21. Скачать презентацию



 Решение квадратных уравнений содержащих параметры в 9 классе
Решение квадратных уравнений содержащих параметры в 9 классе Сложение и вычитание чисел с переходом через десяток
Сложение и вычитание чисел с переходом через десяток Preobrazovanie_grafikov_chislovykh_funktsiy
Preobrazovanie_grafikov_chislovykh_funktsiy Координаты вектора. Параллелограмм
Координаты вектора. Параллелограмм Самостоятельная деятельность учащихся на уроках математики
Самостоятельная деятельность учащихся на уроках математики Деление суммы на число
Деление суммы на число Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Анализ геометрических высказываний
Анализ геометрических высказываний Правильные многоугольники
Правильные многоугольники Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Деление чисел
Деление чисел Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла Метрология. Погрешность измерений
Метрология. Погрешность измерений Простейшие линейные цепи при гармоническом воздействии
Простейшие линейные цепи при гармоническом воздействии 08.09
08.09 Многогранник и тела вращения. Тетраэдр, пирамида, цилиндр, конус, сфера и шар
Многогранник и тела вращения. Тетраэдр, пирамида, цилиндр, конус, сфера и шар Подобные треугольники
Подобные треугольники Многогранник с двумя основаниями
Многогранник с двумя основаниями Измерение массы (для детей 6 лет)
Измерение массы (для детей 6 лет) Свойства функций
Свойства функций Проценты. 6 класс
Проценты. 6 класс Таблица сложения чисел с переходом через десяток. Тренажёр
Таблица сложения чисел с переходом через десяток. Тренажёр Презентация на тему Квадрат (2 класс)
Презентация на тему Квадрат (2 класс)  Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Симметрия в окружающем нас мире
Симметрия в окружающем нас мире Применение мультимедийных презентаций для закрепления навыка оформления краткой записи задачи и её решения. Модуль 2
Применение мультимедийных презентаций для закрепления навыка оформления краткой записи задачи и её решения. Модуль 2