Слайд 2Любые изделия в процессе производства описываются, прежде всего, геометрическими параметрами, без этого

производство невозможно.
Основами для геометрического описания изделий являются: Евклидова геометрия, начертательная геометрия и проекционное черчение, а также аналитическая геометрия.
Традиционный способ геометрического моделирования состоял в применении линейки, циркуля и транспортира на чертёжной доске, объединённых в чертёжный прибор – кульман.
Использование ЭВМ позволило объединить вопросы геометрического моделирования и вычислительной геометрии с использованием векторного (аналитического) описания геометрической информации.
Многократно упростились такие вопросы как построение геометрических элементов, копирование фрагментов, редактирование графической и текстовой информации, штриховка, нанесение размеров, улучшилось качество исполняемых документов.
Слайд 3Во многих приложениях машинной графики возникает потребность в представлении трехмерных тел (вычислительный

эксперимент, автоматизация проектирования, роботизация, вычислительная томография, тренажеры, видеографика и т.д.).
Слайд 4Области применения
В настоящее время геометрическое моделирование успешно используется в управлении и других

областях человеческой деятельности. Можно выделить две основные области применения геометрического моделирования: проектирование и научные исследования.
Одной из самых широких областей применения геометрического моделирования в САПР является синтез и анализ пространственных форм проектируемых объектов
Слайд 5Геометрическое моделирование – раздел математического моделирования – позволяет решать разнообразные задачи в двумерном,

трехмерном и, в общем случае, в многомерном пространстве.
Имеет своей целью описание элементов и явлений, обладающих геометрическими свойствами, поскольку наиболее естественным для них является графическое представление.
Данное моделирование, используется в САПР для решения многих задач: визуализации, построения расчетных сеток, генерации управляющих программ ЧПУ и т.д.
Слайд 6Задачи
Можно выделить две основные задачи, связанные с представлением трехмерных тел:
1) построение модели

уже существующего объекта
При решении первой задачи в общем случае может потребоваться задание бесконечного количества координат точек. Чаще же всего объект с той или иной точностью аппроксимируют некоторым конечным набором элементов, например, поверхностей, тел и т.п.
Слайд 7
2) синтез модели заранее не существовавшего объекта.
При решении второй задачи, выполняемой чаще

всего в интерактивном режиме, основное требование к средствам формирования и представления модели — удобство манипулирования.
Слайд 8Среди задач геометрического моделирования, инвариантных по отношению к объектно-ориентированным приложениям, выделим следующие:

,
1) представление математических моделей, характеризующих структуру, форму и положение пространственных объектов;
2) реализация базовых операций геометрических расчетов и анализа объектов;
3) постановка и решение задач проектирования пространственных форм на основе композиционного подхода.
Слайд 9Геометрическая модель включает в себя системы уравнений и алгоритмы их реализации.
Математической основой

построения модели являются уравнения, описывающие форму и движение объектов.
Все многообразие геометрических объектов является комбинацией различных примитивов – простейших фигур, которые в свою очередь состоят из графических элементов - точек, линий и поверхностей.
Слайд 10Типы моделей
Используются три основных типа 3D моделей:
каркасное представление, когда тело описывается

набором ребер,
поверхностное, когда тело описывается набором ограничивающих его поверхностей,
модель сплошных тел, когда тело формируется из отдельных базовых геометрических и, возможно, конструктивно - технологических объемных элементов с помощью операций объединения, пересечения, вычитания и преобразований.
Слайд 11Геометрические модели нередко имеют иерархическую структуру, возникающую в процессе построения по принципу

- снизу - вверх.
Отдельные компоненты используются как строительные блоки для формирования объектов более высокого уровня, которые, в свою очередь, могут использоваться для объектов еще более высокого уровня.
В общем случае геометрические модели подразделяются на двумерные и трехмерные.










 Теория вероятностей, подготовка к ЕГЭ - 2019
Теория вероятностей, подготовка к ЕГЭ - 2019 Факторный анализ
Факторный анализ Теория вероятностей
Теория вероятностей Презентация на тему Игра по теме "Степень и ее свойства"
Презентация на тему Игра по теме "Степень и ее свойства"  Математическая сказка. День рождения
Математическая сказка. День рождения Тригонометрически уравнения
Тригонометрически уравнения Частные производные
Частные производные Группировки в историческом исследовании
Группировки в историческом исследовании Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Тригонометрические функции
Тригонометрические функции Сравнение множеств
Сравнение множеств Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Обратные тригонометрические функции
Обратные тригонометрические функции Логарифмическая функция. Свойства, график. Решение примеров
Логарифмическая функция. Свойства, график. Решение примеров Деление дробей. Решение задач
Деление дробей. Решение задач Математические модели и методы их решения (тема 6)
Математические модели и методы их решения (тема 6) Сокращенное умножение многочленов
Сокращенное умножение многочленов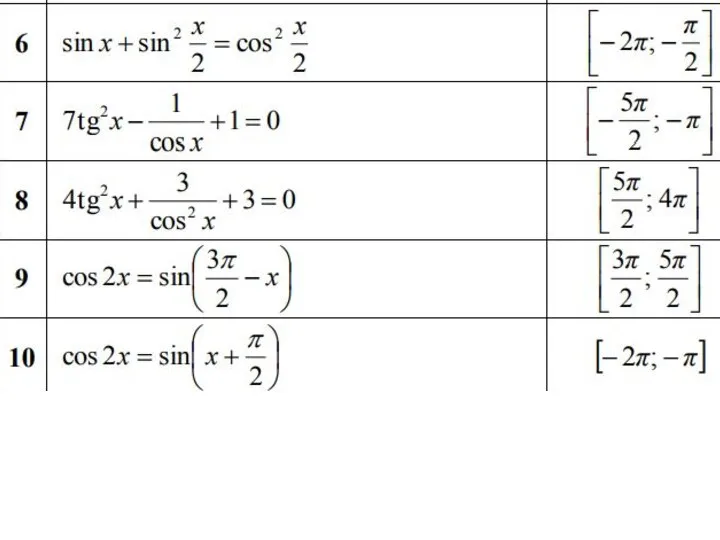 Решение уравнений
Решение уравнений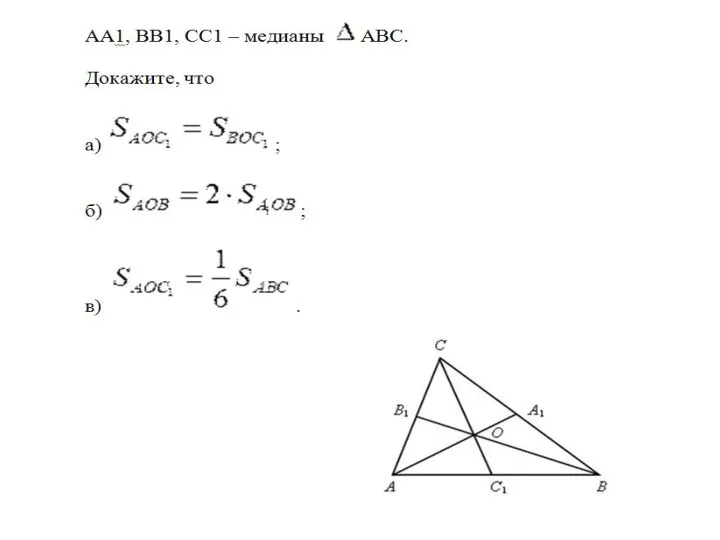 Примеры подобия к доказательству теорем и решению задач. Урок 39
Примеры подобия к доказательству теорем и решению задач. Урок 39 Понятие цилиндра и конуса
Понятие цилиндра и конуса Многоугольники в нашей жизни
Многоугольники в нашей жизни Презентация на тему Числовые и буквенные выражения (5 класс)
Презентация на тему Числовые и буквенные выражения (5 класс)  Математика вокруг нас. Геометрический облик бульвара имени академика Кикоина
Математика вокруг нас. Геометрический облик бульвара имени академика Кикоина Кривые второго порядка. Практика
Кривые второго порядка. Практика Тақырып 3 Минорлар және алгебралық толықтауыштар
Тақырып 3 Минорлар және алгебралық толықтауыштар Решение задач с помощью уравнений. Устные вычисления
Решение задач с помощью уравнений. Устные вычисления Решение заданий №17 ЕГЭ профильной математики (задания с параметром)
Решение заданий №17 ЕГЭ профильной математики (задания с параметром)