Содержание
- 2. Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех x из этого промежутка
- 3. Показать, что функция является первообразной для функции Решение:
- 4. Показать, что функция является первообразной для функции Решение:
- 5. Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция F(x)+C также является первообразной функции
- 11. Правила нахождения первообразных
- 12. Если F(x)– первообразная для функции f(x), а G(x)– первообразная для функции g(x), то F(x)+G(x)– первообразная для
- 13. Если F(x)– первообразная для функции f(x), а а –константа, то аF(x)– первообразная для функции аf(x) Постоянный
- 14. Если F(x) – первообразная для функции f(x), а k и b- константы, причем то -первообразная для
- 16. Скачать презентацию




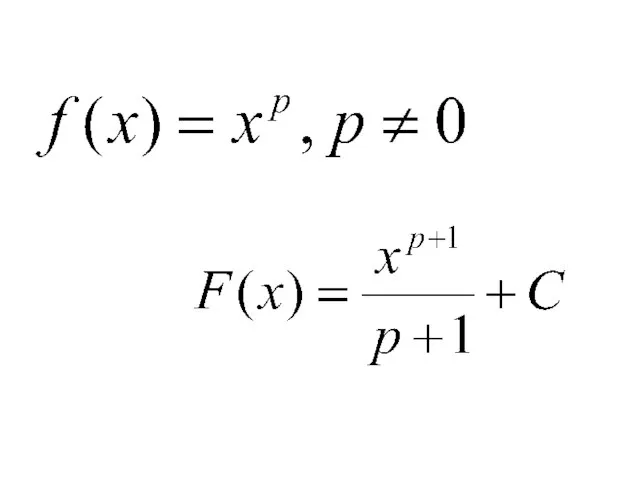
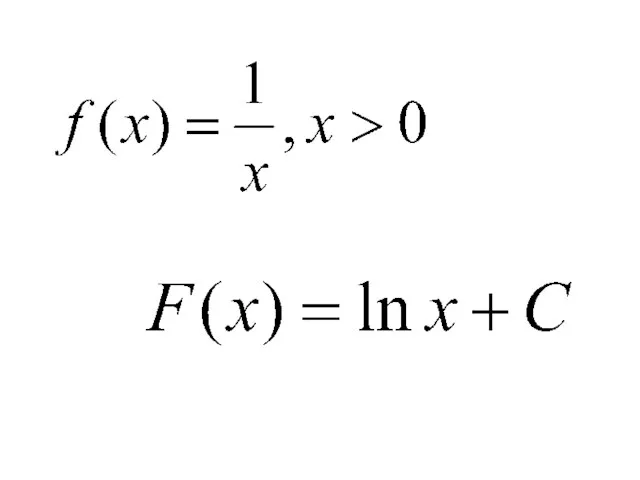
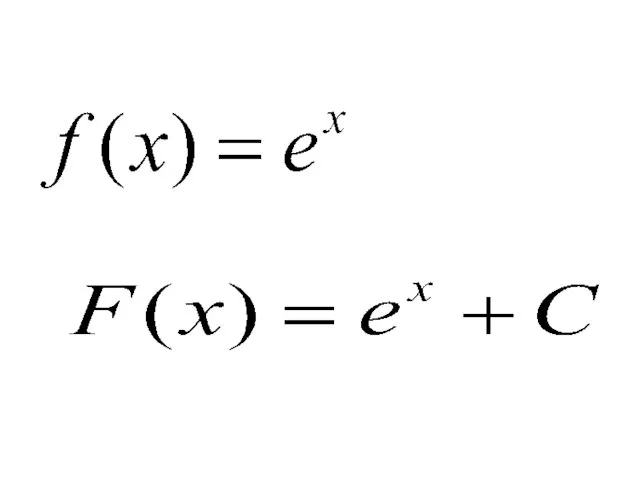
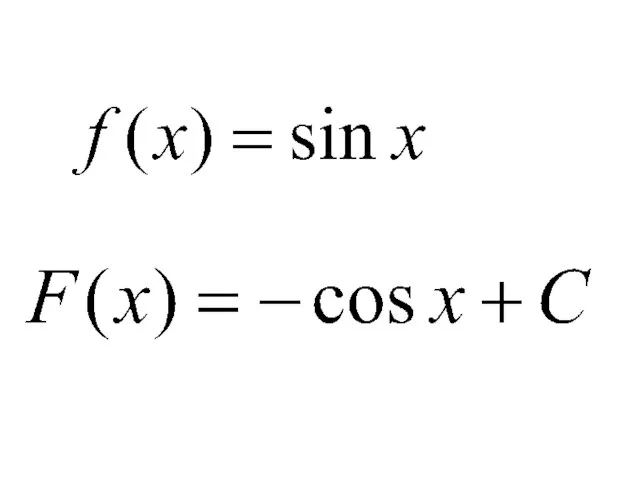
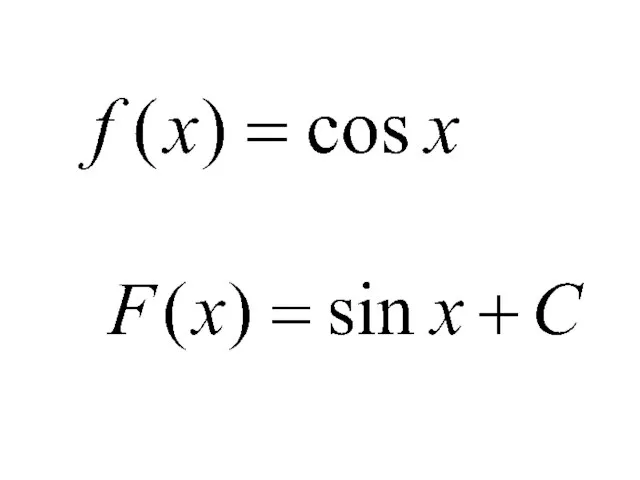




 Геометрия в живописи
Геометрия в живописи Теория вероятностей
Теория вероятностей Условный оператор задач
Условный оператор задач Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Время. Решение задач
Время. Решение задач Математика вокруг нас
Математика вокруг нас Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен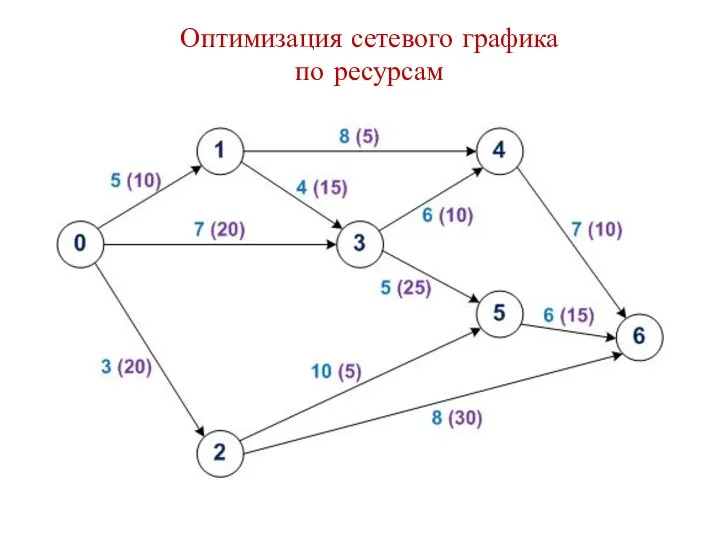 Оптимизация сетевого графика по ресурсам
Оптимизация сетевого графика по ресурсам Построение сечений
Построение сечений Тела вращения. Использование ИКТ
Тела вращения. Использование ИКТ МЕТОДИКА ИСПОЛЬЗОВАНИЯ ДИДАКТИЧЕСКИХ ИГР НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
МЕТОДИКА ИСПОЛЬЗОВАНИЯ ДИДАКТИЧЕСКИХ ИГР НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ Ломаная линия. Обозначение ломаной
Ломаная линия. Обозначение ломаной Таблица значений синуса, косинуса, тангенса для углов
Таблица значений синуса, косинуса, тангенса для углов Арифметическая прогрессия
Арифметическая прогрессия Задания Незнайки
Задания Незнайки Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ»
Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ» Делимость чисел. НОК
Делимость чисел. НОК Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи Презентация на тему Длина окружности и площадь круга (9 класс)
Презентация на тему Длина окружности и площадь круга (9 класс)  Параллельный перенос
Параллельный перенос Действия с дробями. Устная работа
Действия с дробями. Устная работа Первый признак параллельности прямых
Первый признак параллельности прямых Презентация на тему Перестановка слагаемых (1 класс)
Презентация на тему Перестановка слагаемых (1 класс)  Натуральные числа и их обозначение
Натуральные числа и их обозначение Случайный выбор точки из отрезка
Случайный выбор точки из отрезка Это полезно знать
Это полезно знать Выражение отношения в процентах
Выражение отношения в процентах Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс