Содержание
- 2. Криволинейной трапецией называется фигура, ограниченная отрезками прямых х = а, х = b, y = 0
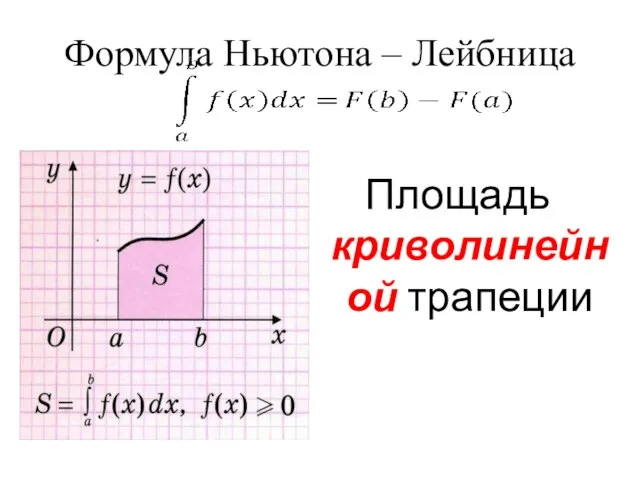
- 3. Формула Ньютона – Лейбница Площадь криволинейной трапеции
- 4. Вычислить площадь криволинейной трапеции
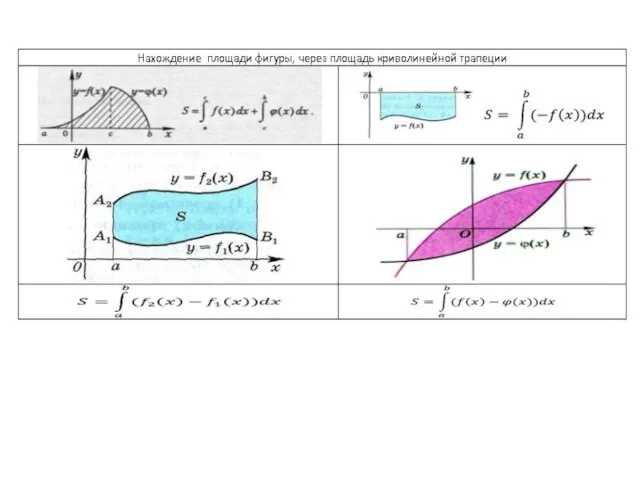
- 5. Площадь фигуры равна сумме площадей криволинейных трапеций
- 6. Площадь фигуры равна разности площадей криволинейных трапеций
- 7. Площадь фигуры вычисляется как разность площадей криволинейных трапеций на отрезке [a;b] Если функции у = f(x)
- 8. Искомая площадь фигуры равна площади фигуры, симметричной данной относительно оси Ох Если f(x) 0 на отрезке
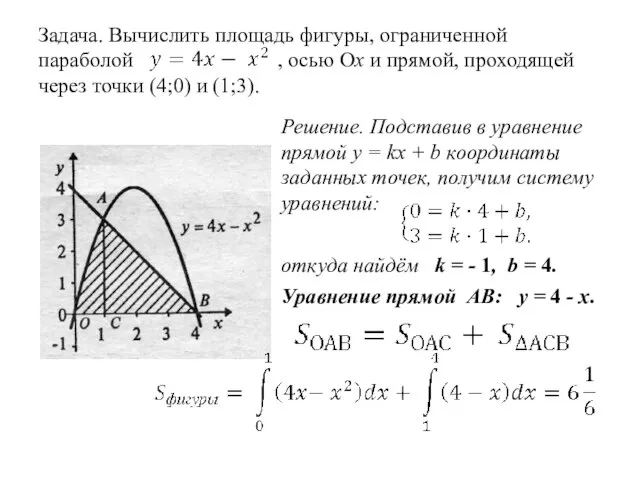
- 10. Задача. Вычислить площадь фигуры, ограниченной параболой , осью Ох и прямой, проходящей через точки (4;0) и
- 11. Задача. Вычислить площадь фигуры, ограниченной параболой , осью Ох и прямой, проходящей через точки (4;0) и
- 12. Задача. Найти площадь фигуры, ограниченной линиями Решение. Точки пересечения заданных линий: О(0;0), К(6;0), Р(4;2) Фигура состоит
- 13. Решение. Найдём абсциссы точек пересечения этих графиков из уравнения Искомая площадь равна сумме площадей криволинейных трапеций
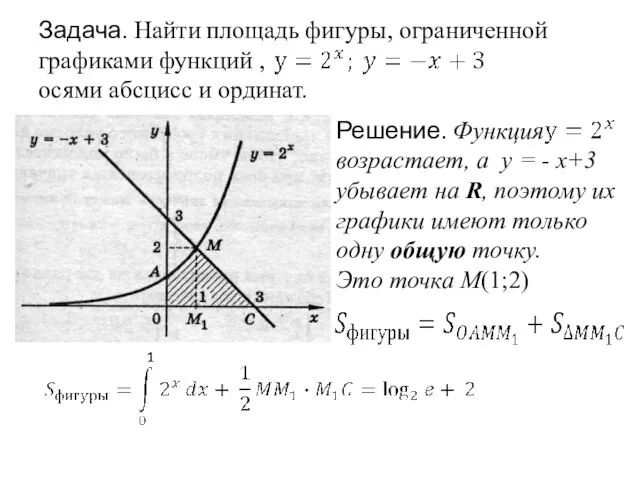
- 14. Задача. Найти площадь фигуры, ограниченной графиками функций , осями абсцисс и ординат. Решение. Функция возрастает, а
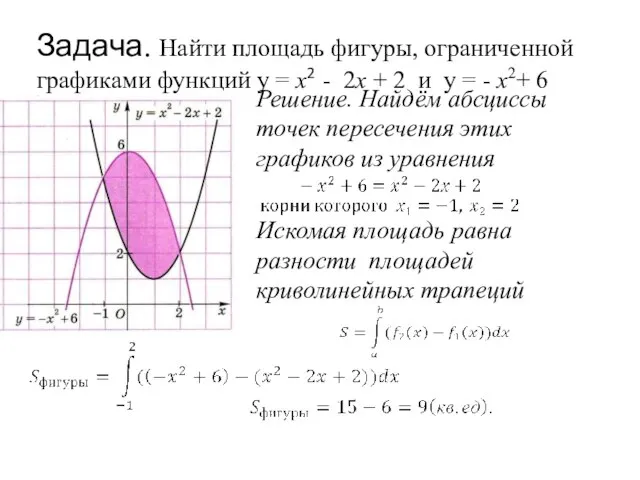
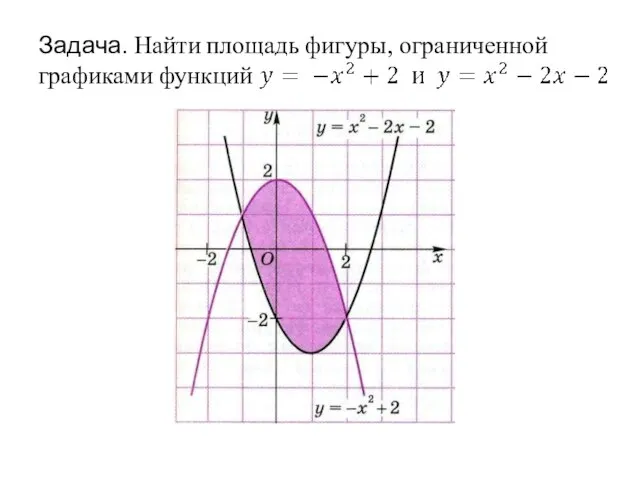
- 15. Задача. Найти площадь фигуры, ограниченной графиками функций y = x2 - 2x + 2 и y
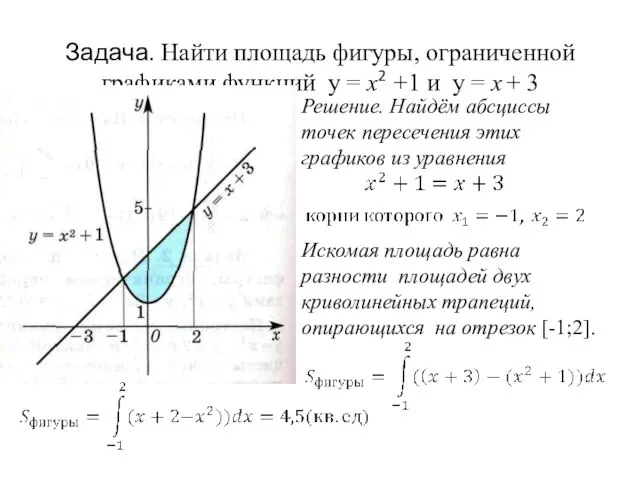
- 16. Задача. Найти площадь фигуры, ограниченной графиками функций y = x2 +1 и y = x +
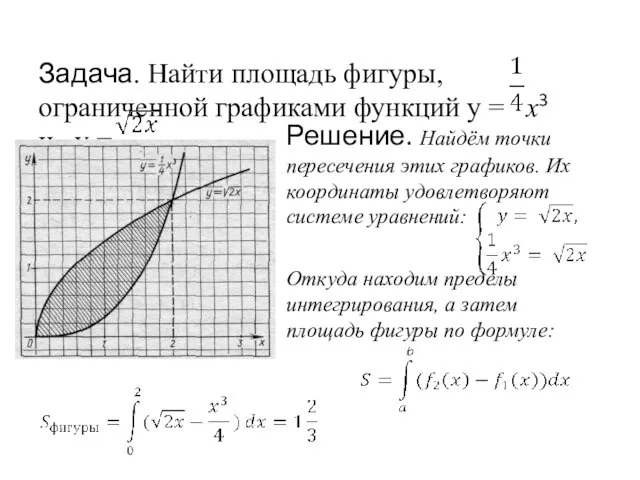
- 17. Задача. Найти площадь фигуры, ограниченной графиками функций y = x3 и y = Решение. Найдём точки
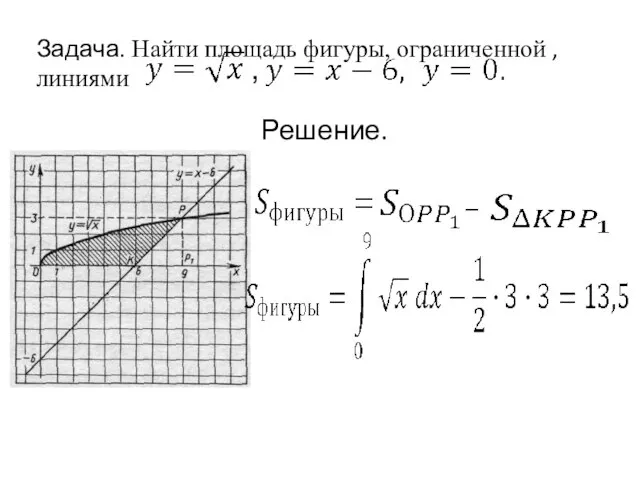
- 18. Задача. Найти площадь фигуры, ограниченной , линиями , – Решение.
- 19. Задача. Найдите площадь фигуры, ограниченной линиями Решение.
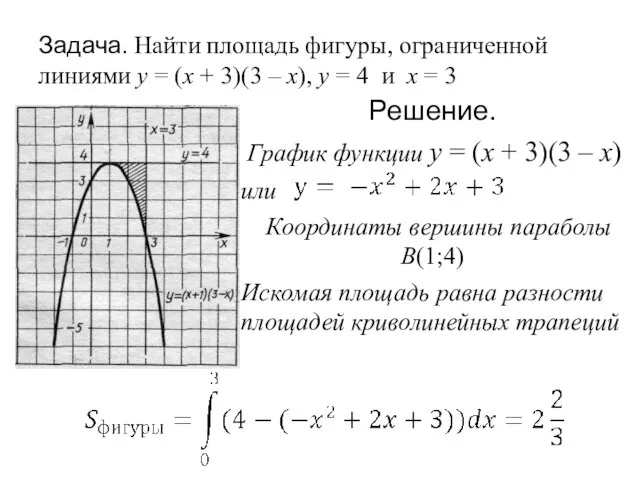
- 20. Задача. Найти площадь фигуры, ограниченной линиями y = (x + 3)(3 – x), y = 4
- 21. Задача. Найти площадь фигуры, ограниченной графиком функции и осями координат Решение. Заданная фигура представляет собой криволинейную
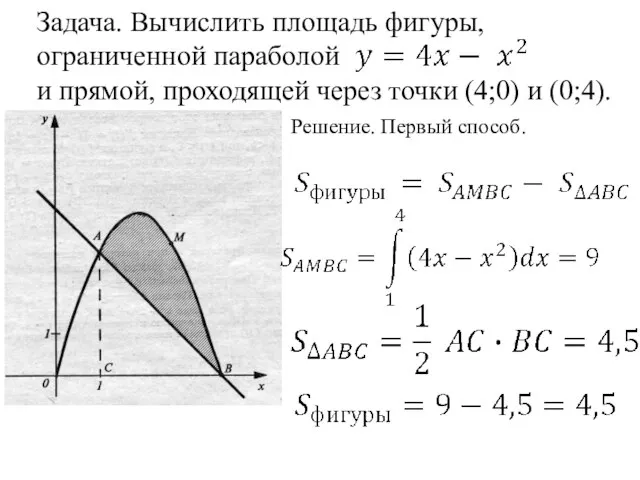
- 22. Задача. Вычислить площадь фигуры, ограниченной параболой и прямой, проходящей через точки (4;0) и (0;4). Решение. Первый
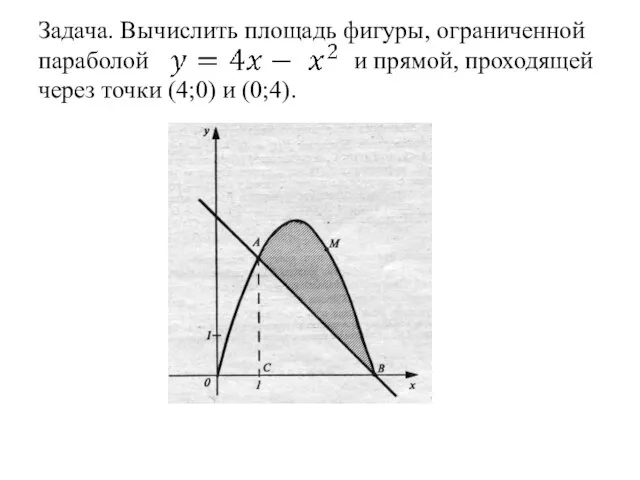
- 23. Задача. Вычислить площадь фигуры, ограниченной параболой и прямой, проходящей через точки (4;0) и (0;4).
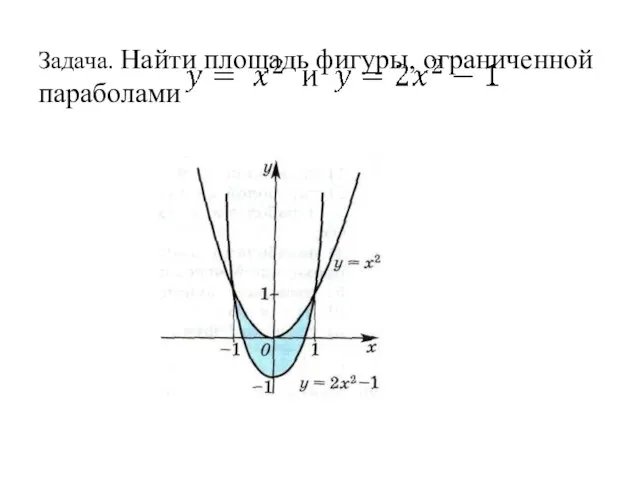
- 24. Задача. Найти площадь фигуры, ограниченной параболами
- 25. Задача. Найти площадь фигуры, ограниченной графиками функций
- 26. По рисункам 31 – 36 назвать из каких фигур состоит фигура , площадь которой вычисляется, и
- 28. Скачать презентацию




![Площадь фигуры вычисляется как разность площадей криволинейных трапеций на отрезке [a;b] Если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/839124/slide-6.jpg)







 Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  Задача линейного программирования. Канонический вид задачи линейного программирования
Задача линейного программирования. Канонический вид задачи линейного программирования Производная функции. Геометрический смысл производной. Механический смысл производной
Производная функции. Геометрический смысл производной. Механический смысл производной Численные методы решения СЛАУ (часть 2)
Численные методы решения СЛАУ (часть 2) Цифры
Цифры Ряды распределения в статистике
Ряды распределения в статистике Решение задач
Решение задач Точка перегиба
Точка перегиба Метод координат на плоскости
Метод координат на плоскости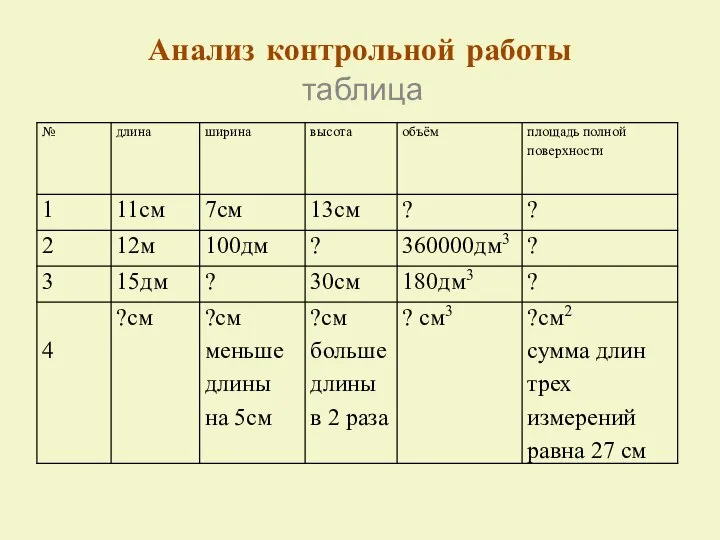 Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Неравенство треугольника
Неравенство треугольника Морское путешествие
Морское путешествие Понятия много и один. Число и цифра 1
Понятия много и один. Число и цифра 1 Векторы
Векторы Подготовка к ЕГЭ В8
Подготовка к ЕГЭ В8 Понятия длиннее, короче, одинаковые по длине
Понятия длиннее, короче, одинаковые по длине Основные понятия метода статистического моделирования: случайное число от 0 до 1, его свойства, примеры датчиков случайных чисел
Основные понятия метода статистического моделирования: случайное число от 0 до 1, его свойства, примеры датчиков случайных чисел Теорема Пифагора
Теорема Пифагора Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка Неполные квадратные уравнения
Неполные квадратные уравнения Множества (числовые и не только)
Множества (числовые и не только)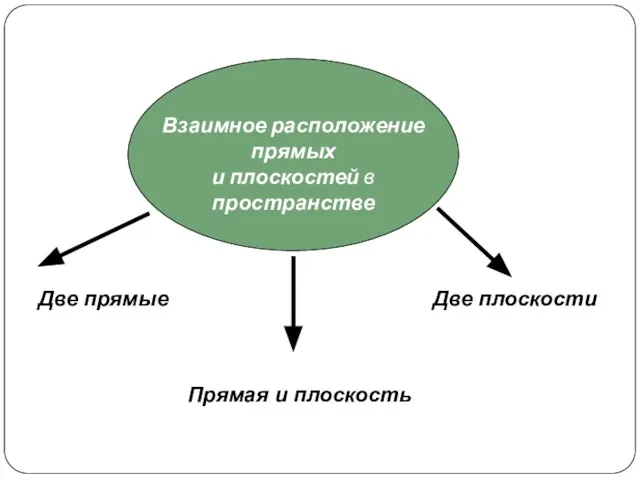 Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Алгебраические и геометрические модели
Алгебраические и геометрические модели Решение уравнений
Решение уравнений Математическая спартакиада
Математическая спартакиада Сравнение числовых выражений (Урок 30)
Сравнение числовых выражений (Урок 30) 2.7. Теория систем линейных алгебраических уравнений
2.7. Теория систем линейных алгебраических уравнений