Содержание
- 2. Математическая статистика
- 5. Медиана
- 8. Домашнее задание Ч1 статистика Десятичные дроби
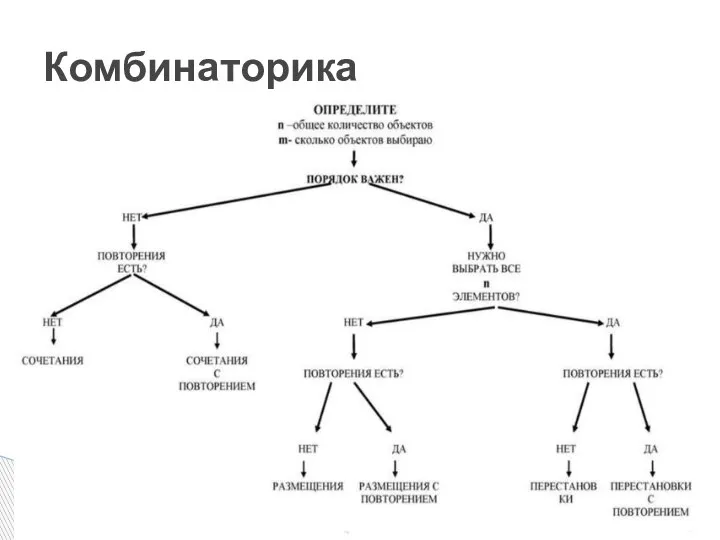
- 9. Комбинаторика
- 10. Комбинаторика
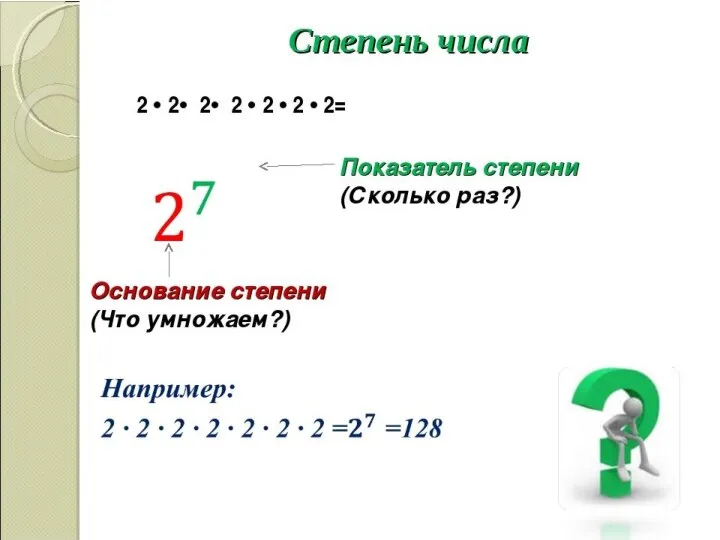
- 12. При решении некоторых задач удобно использовать посчитанные значения факториала (например, на перестановку без повторений)
- 14. 3 * 3 = 9 2 * 2* 2 =8
- 15. Задание + разбор 1
- 16. Задание + разбор 2
- 17. Домашнее задание ч 2 степень
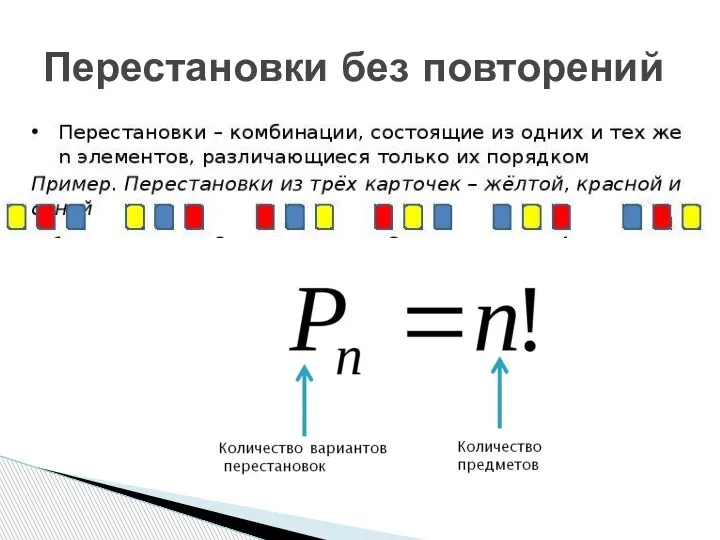
- 18. Перестановки без повторений
- 19. Перестановки без повторений Количество предметов n = 3 (красная, жёлтая и синяя карточки) Количество вариантов перестановок
- 20. Домашнее задание 1.1 Сколько лет понадобится этой компании молодых людей, если они будут приходить каждый день?
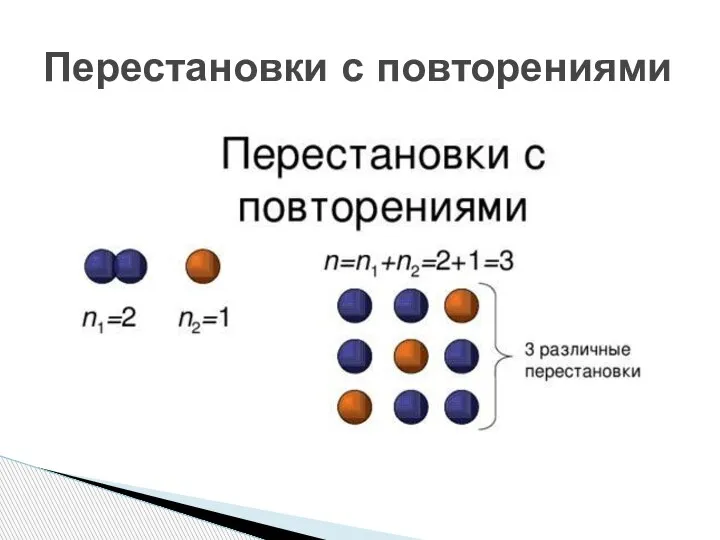
- 21. Перестановки с повторениями
- 22. Перестановки с повторениями
- 23. Перестановки с повторениями Всего шариков 3, то есть n = 3 Одинаковых шариков (повторений) k=2
- 24. Перестановки с повторениями
- 25. Сколько различных браслетов можно сделать из пяти одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров
- 26. Перестановки с повторениями Всего 18 камней изумрудов 5 рубинов 6 сапфиров 7 n = 18 k1
- 27. Перестановки с повторениями 4 3 3 11* 12 * 13* 14 * 3 * 4 *
- 28. Домашнее задание 1.2 Анаграмма — это слово (не обязательно осмысленное), полученное из данного слова перестановкой букв.
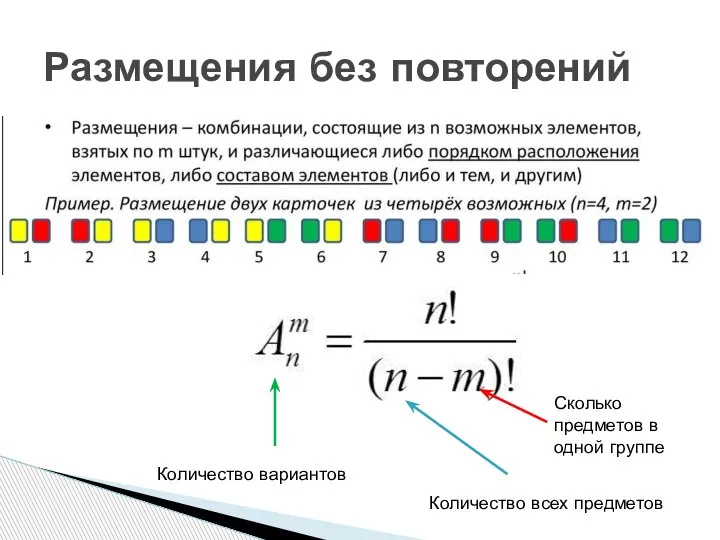
- 29. Размещения без повторений Количество вариантов Количество всех предметов Сколько предметов в одной группе
- 30. Размещения без повторений Всего карточек 4 (желтая, красная, синяя и зелёная) В группе по две карточки
- 31. Размещения без повторений Всего разных дисциплин 11, значит, n=11 За день может быть 5 предметов, значит,
- 32. Домашнее задание 2.1 Эти города входят в «Золотое кольцо России» — туристский маршрут, проходящий по древним
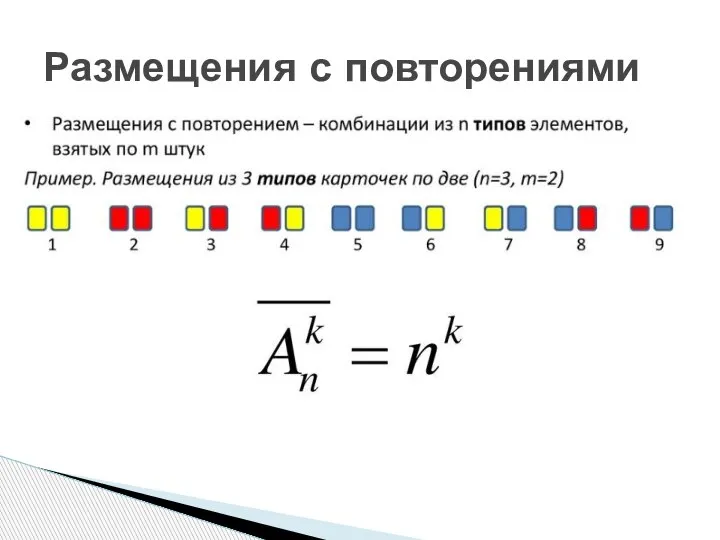
- 33. Размещения с повторениями
- 34. Размещения с повторениями Всего букв 12, значит, n =12 В номере по три буквы, значит, k
- 35. Домашнее задание 2.2
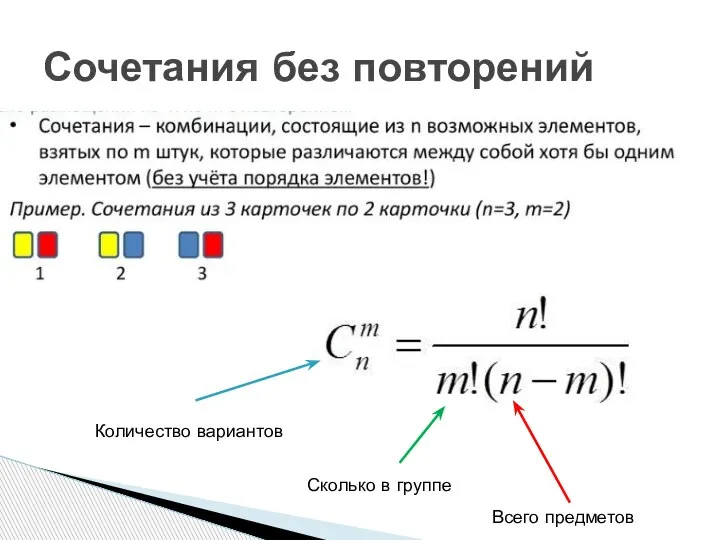
- 36. Сочетания без повторений Количество вариантов Всего предметов Сколько в группе
- 37. Сочетания без повторений Всего карточек 3 (жёлтая, синяя и красная) В группе по 2 карточки n
- 38. Сочетания без повторений
- 39. Сочетания без повторений Всего разных соков 5, значит, n=5 В каждом коктейле 3 сока, значит, m=3
- 40. Домашнее задание 3.1 Сколькими способами можно выбрать троих футболистов из 11 для прохождения допинг-контроля? В Древней
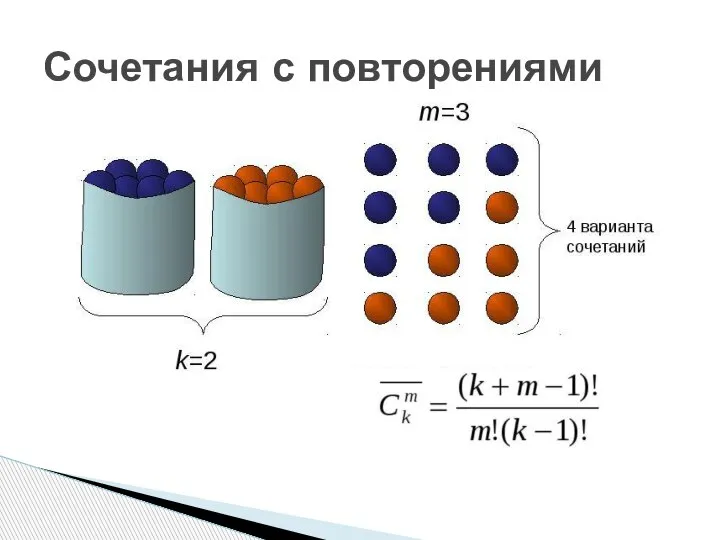
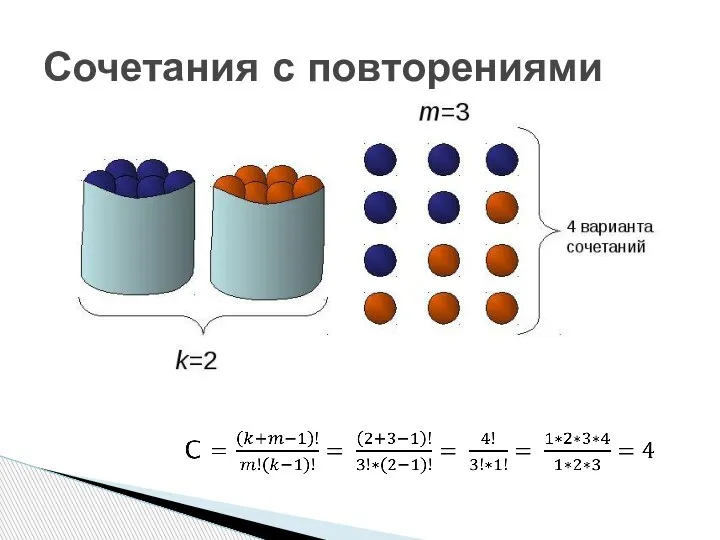
- 41. Сочетания с повторениями
- 42. Сочетания с повторениями
- 43. Сочетания с повторениями В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?
- 44. Сочетания с повторениями В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных? 3
- 46. Скачать презентацию


































 Признаки равенства треугольников
Признаки равенства треугольников Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Математический диктант по теме первый признак равенства треугольников. Геометрия. 7 класс
Математический диктант по теме первый признак равенства треугольников. Геометрия. 7 класс Окружность, круг и их элементы. Готовимся к ОГЭ, задание 16
Окружность, круг и их элементы. Готовимся к ОГЭ, задание 16 Цифровой образовательный ресурс по алгебре. 8 класс
Цифровой образовательный ресурс по алгебре. 8 класс Имитационное моделирование
Имитационное моделирование Алан Тьюринг
Алан Тьюринг Комбинация фигур
Комбинация фигур Метрология как наука
Метрология как наука Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ
Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ  Свойства алгоритма
Свойства алгоритма Движение
Движение Арктангенс числа
Арктангенс числа Вероятность равновозможных событий
Вероятность равновозможных событий Дидактические игры на уроках математики
Дидактические игры на уроках математики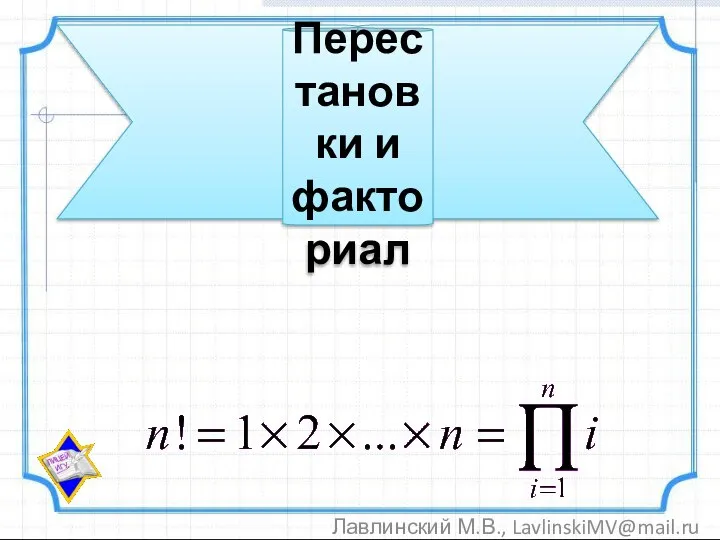 Перестановки и факториал
Перестановки и факториал Опорные конспекты. Геометрия. 10 класс
Опорные конспекты. Геометрия. 10 класс Параллелограм и трапеция
Параллелограм и трапеция Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Движение (9 класс)
Презентация на тему Движение (9 класс)  Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Вспомним планиметрию
Вспомним планиметрию Презентация на тему Упрощение выражений
Презентация на тему Упрощение выражений  Вычитаем числа
Вычитаем числа Меню. Основные простые формы. Общие простые формы
Меню. Основные простые формы. Общие простые формы Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ
Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ  Площадь прямоугольника. Задачи
Площадь прямоугольника. Задачи Графы. Способы задания графов. Степени вершин
Графы. Способы задания графов. Степени вершин