Пропорциональность площадей

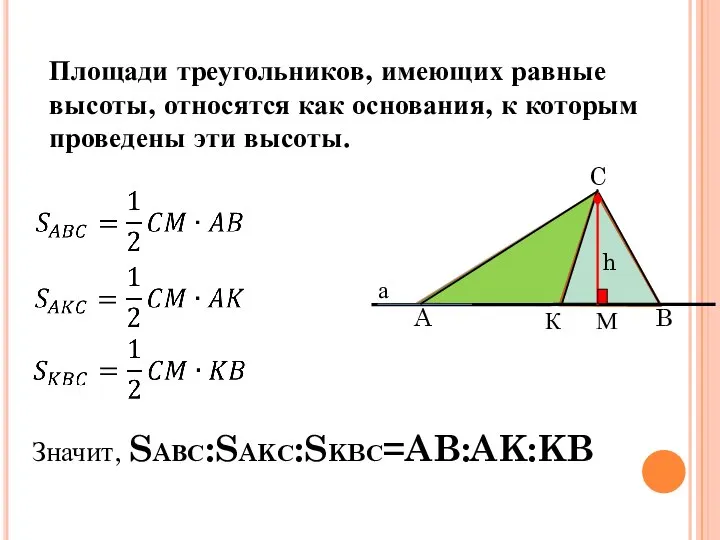
Площадь треугольника
a
Площадь треугольника равна половине произведения основания на высоту, проведенную к данному основанию.

Значит, SAВС:SAKС:SKBС=AB:AK:KB
Пропорциональность площадей
Площади треугольников, имеющих равные высоты, относятся как основания, к которым проведены эти высоты.

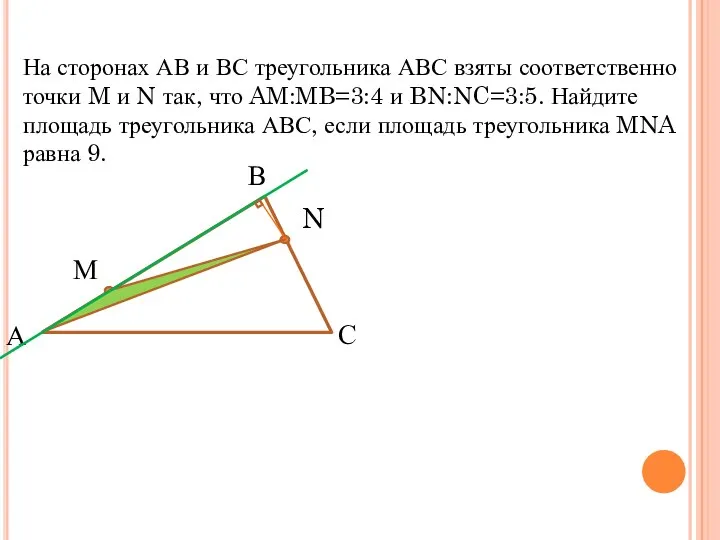
На сторонах АВ и ВС треугольника АВС взяты соответственно точки M и N так, что AM:MB=3:4 и BN:NC=3:5. Найдите площадь треугольника АВС, если площадь треугольника MNA равна 9.
Задача №2
М
N

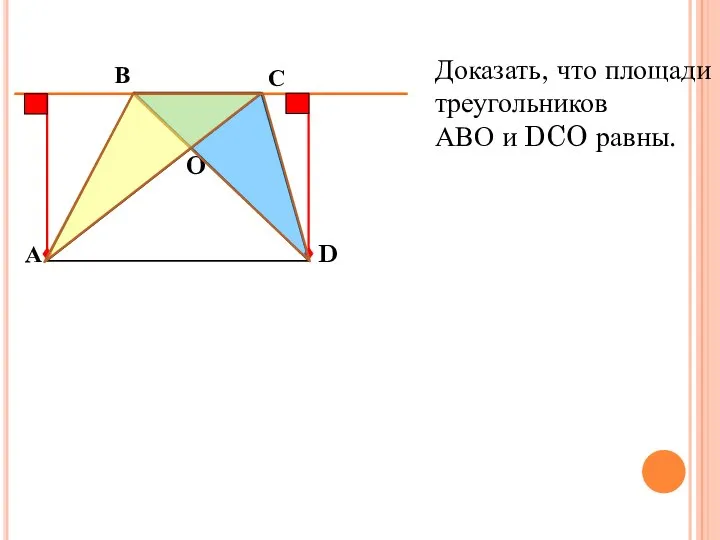
Рассмотреть на уроке
Доказать, что площади треугольников
АВО и DCO равны.

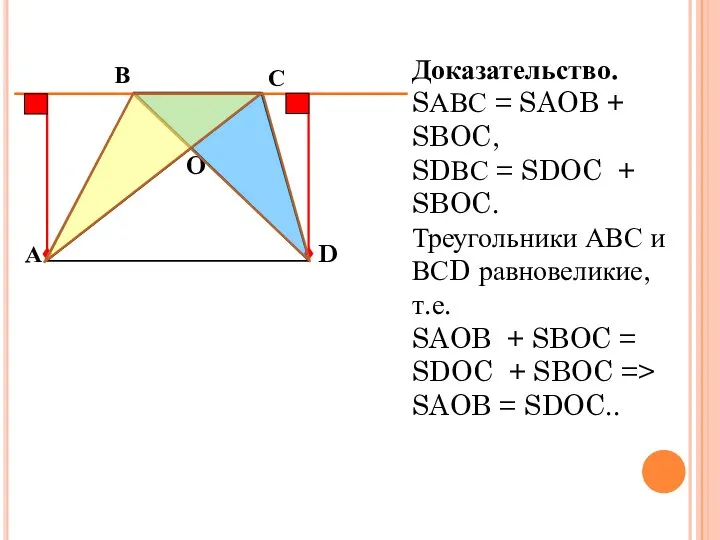
Рассмотреть на уроке
Доказательство.
SАВС = SAOB + SBOC, SDВС = SDOC + SBOC. Треугольники АВС и ВСD равновеликие, т.е.
SAOB + SBOC = SDOC + SBOC => SAOB = SDOC..