Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши)

Подстановки

Вычисление интегралов с переменным верхним пределом

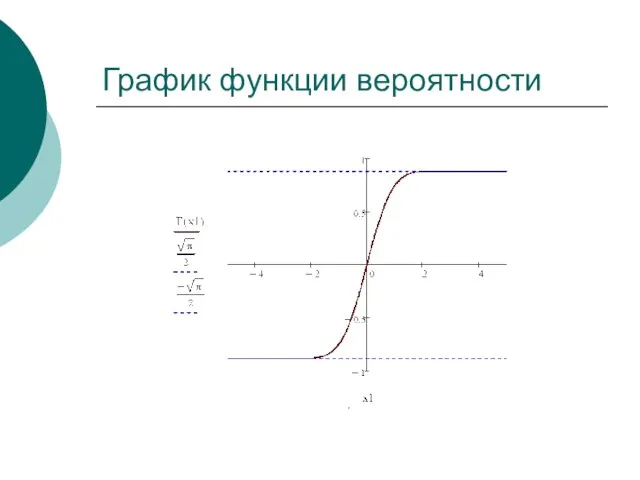
График функции вероятности

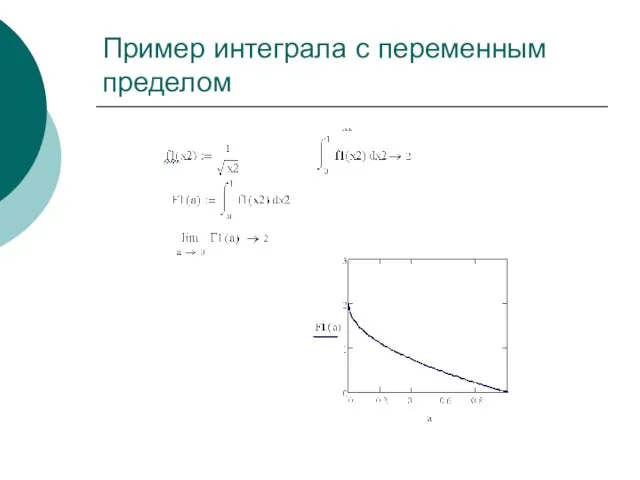
Пример интеграла с переменным пределом

Построение графиков и нахождение параметров уравнений заданных в параметрическом виде

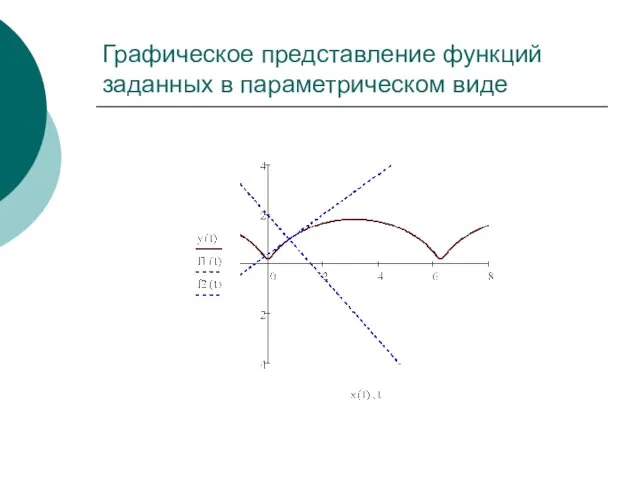
Графическое представление функций заданных в параметрическом виде

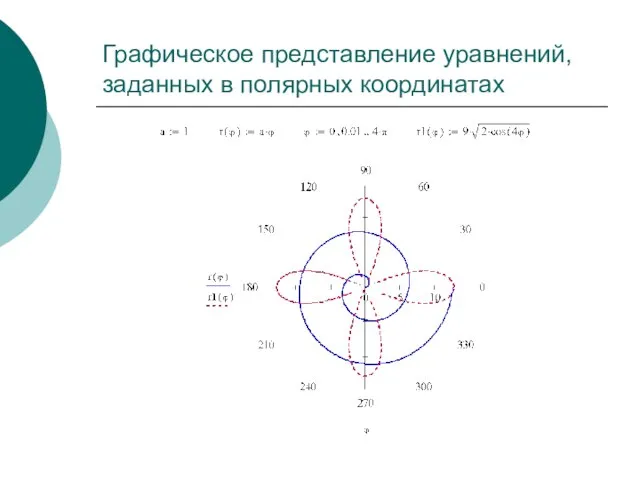
Графическое представление уравнений, заданных в полярных координатах

Оптимизация функций. Классическое решение

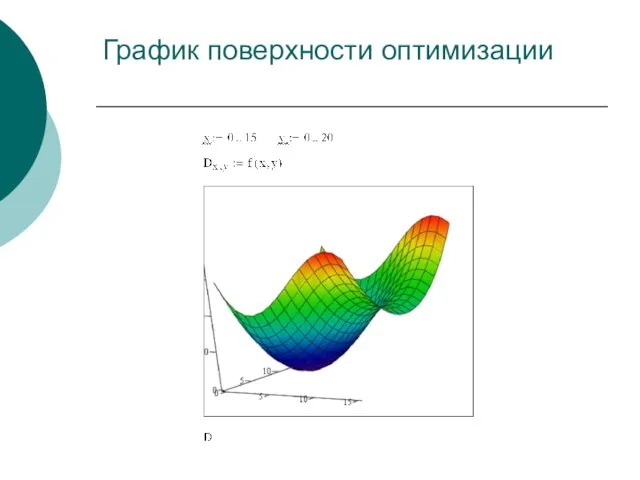
График поверхности оптимизации

Контурный график заданной функции оптимизации

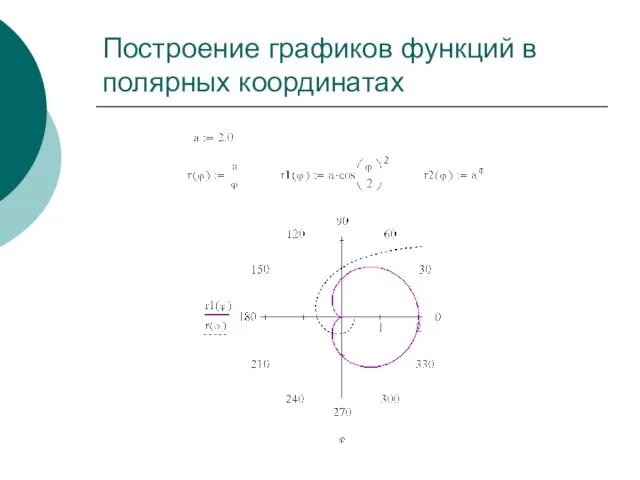
Построение графиков функций в полярных координатах

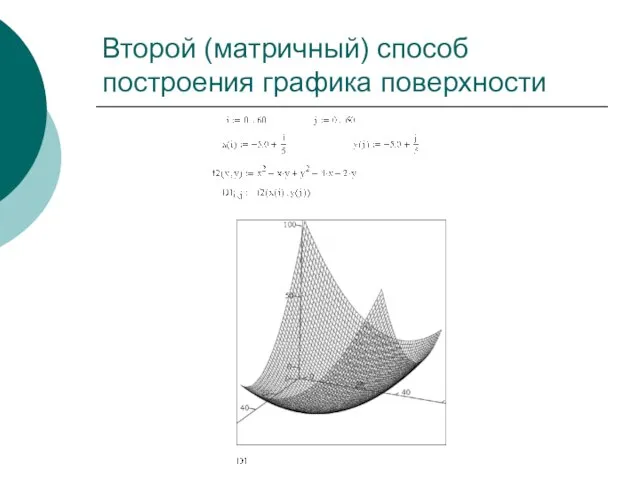
Второй (матричный) способ построения графика поверхности

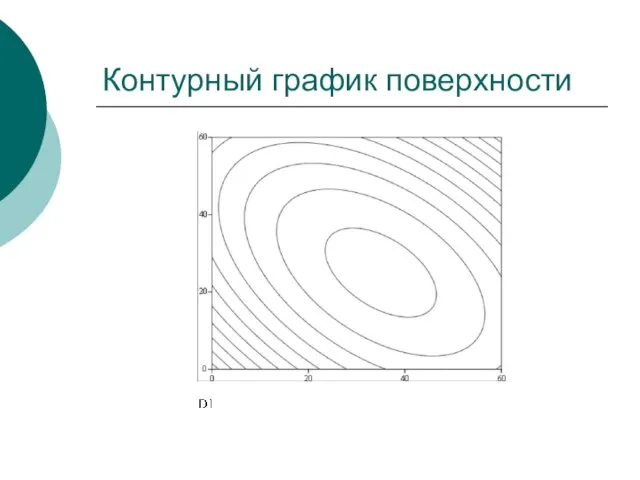
Контурный график поверхности

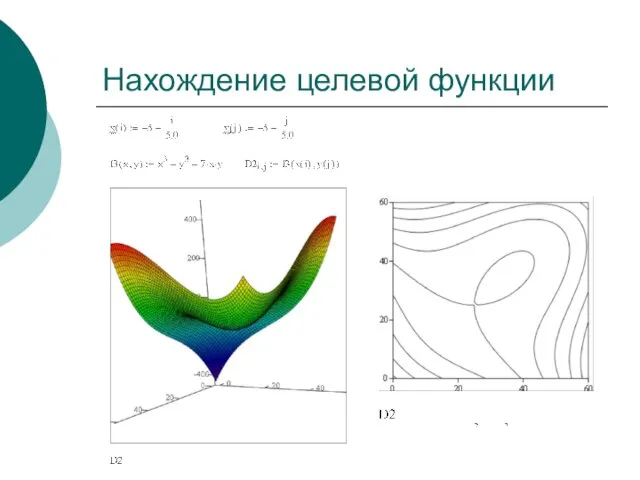
Нахождение целевой функции

Нахождение локального минимума

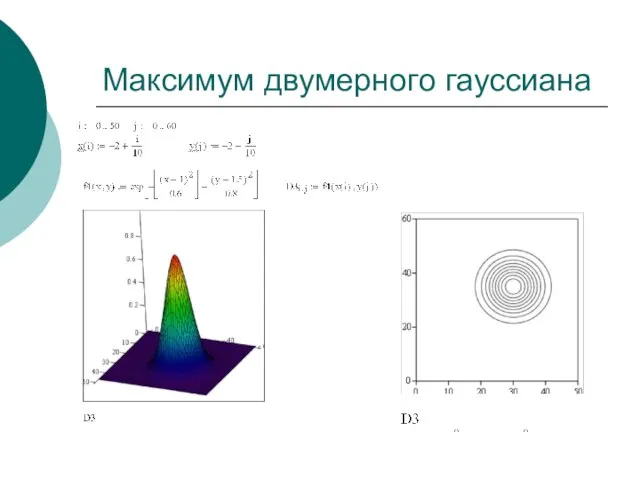
Максимум двумерного гауссиана

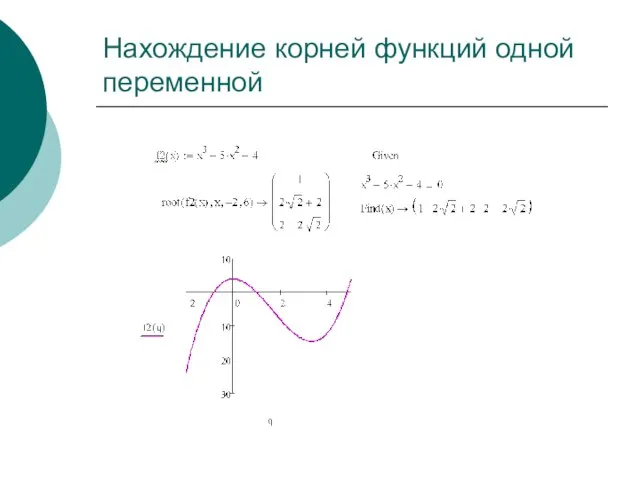
Нахождение корней функций одной переменной

Решение задачи безусловной оптимизации
Р е ш е н и е з а д а ч и б е з у с л о в н о й о п т и м и з а ц и и д л я з а д а н н о й ц е л е в о й ф у н к ц и и д в у х п е р е м е н н ы х f(x) н а м н о ж е с т в е Х .

Нахождение стационарных точек

Построение матрицы Гессе

Построение матрицы Гессе (продолжение). Проверка 1 стационарной точки на экстремум

Проверка матрицей Гессе второй стационарной точки на экстремум

Подтверждение правильности нахождения точки минимума

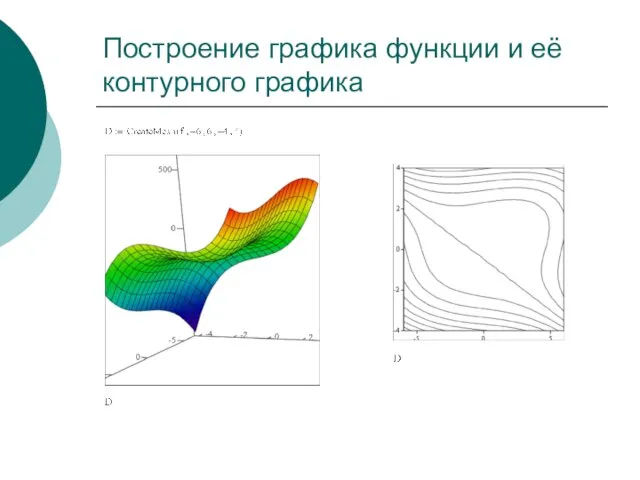
Построение графика функции и её контурного графика

Решение дифференциальных уравнений 1 и 2 –го порядка
Диф уравнение имеет вид: y’ = (1+x*y)/x^2, y(1) = 0, 1<=x<=2
Решение задачи методом Рунге-Кутта предполагает использование функции rkfixed (y, a, b, N, D). a, b – границы отрезка, N - число узлов на сетке.

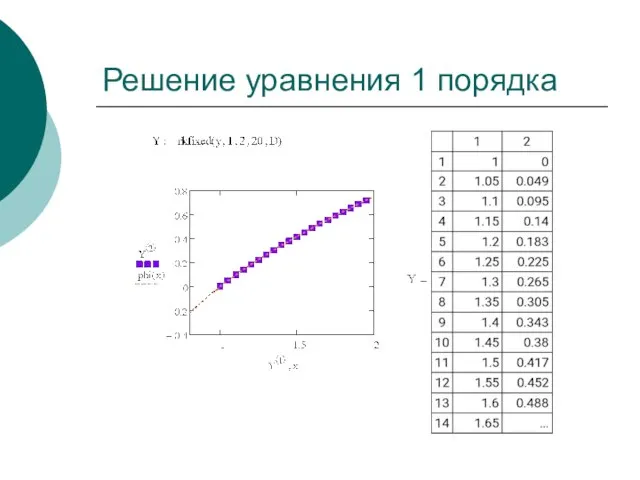
Решение уравнения 1 порядка

Решение однородного уравнения 2 порядка
Уравнение второго порядка имеет вид: xy’’-(x+1)y’-2(x-1)y=0.
Строим вектор-столбец начальных условий и вектор-функцию правых частей:

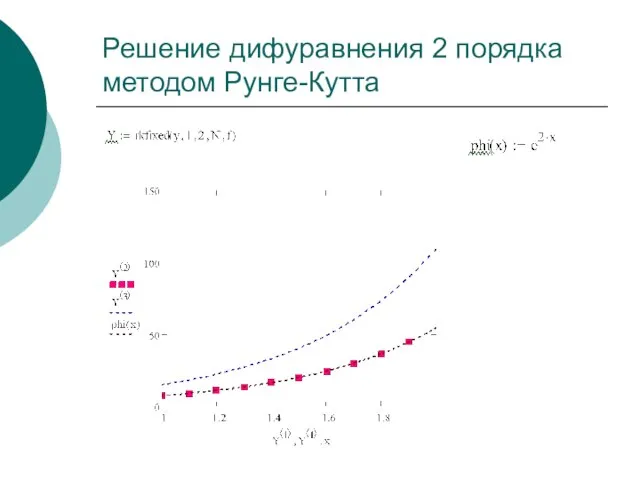
Решение дифуравнения 2 порядка методом Рунге-Кутта

Классическое решение диф. Уравнений с использованием функции Odesolve(x, xend)

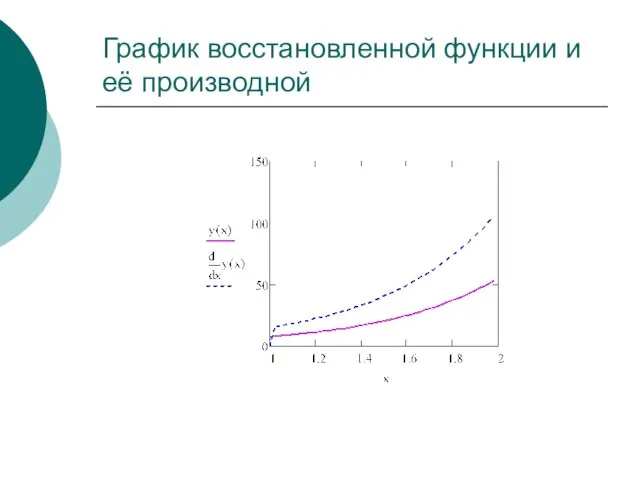
График восстановленной функции и её производной

Решение системы двух дифуравнений первого порядка с начальными условиями.
5. Исследовать поведение системы, моделирующей двухмодовый режим взаимодействия амплитуд полей лазера. Построить фазовую траекторию и режим временной эволюции каждой моды.
Находим решение следующим образом, как показано на рабочей странице MathCad:

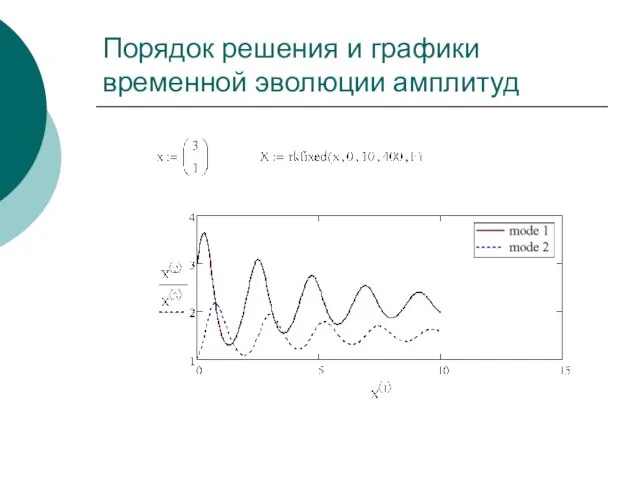
Порядок решения и графики временной эволюции амплитуд

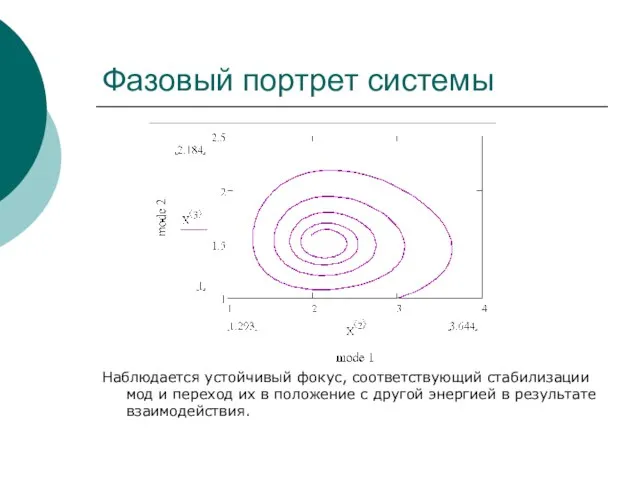
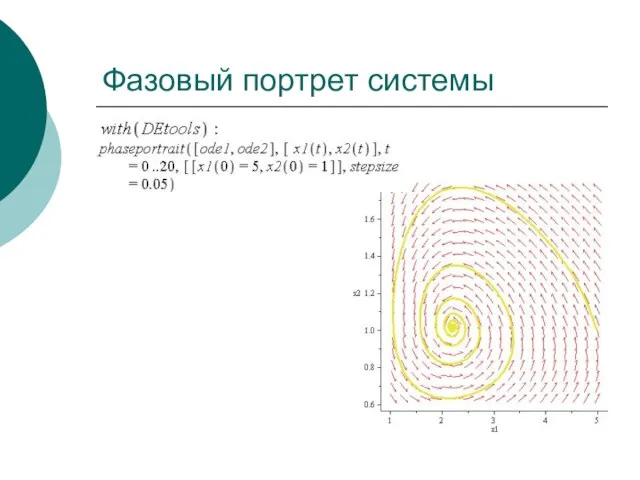
Фазовый портрет системы
Наблюдается устойчивый фокус, соответствующий стабилизации мод и переход их в положение с другой энергией в результате взаимодействия.

Числовой формат вывода
Значение амплитуд в зависимости от времени задается в виде матрицы, состоящей из трех столбцов Y1- время, Y2 – амплитуда моды 1, Y3 – амплитуда моды 2.

Решение дифуравнений в пакете Mathematica v. 7.
DSolve[{x*y''[x]-(x+1)*y'[x]-2*(x)*y[x]==0,y[1]==e^2,y'[1]==2*e^2},y[x],x]

График полученной функции

Решение системы дифуравнений первого порядка в пакете Mathematica v.7

Построение фазового портрета с помощью параметрического графика

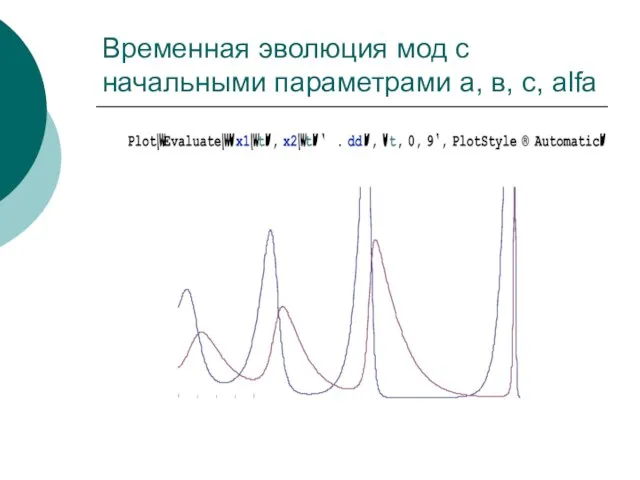
Временная эволюция мод с начальными параметрами а, в, с, alfa

Задание новых параметров задачи

Фазовый портрет системы при слабом взаимодействии мод

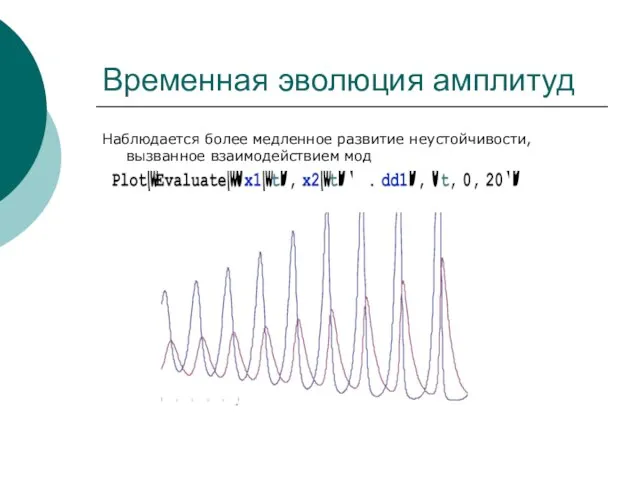
Временная эволюция амплитуд
Наблюдается более медленное развитие неустойчивости, вызванное взаимодействием мод

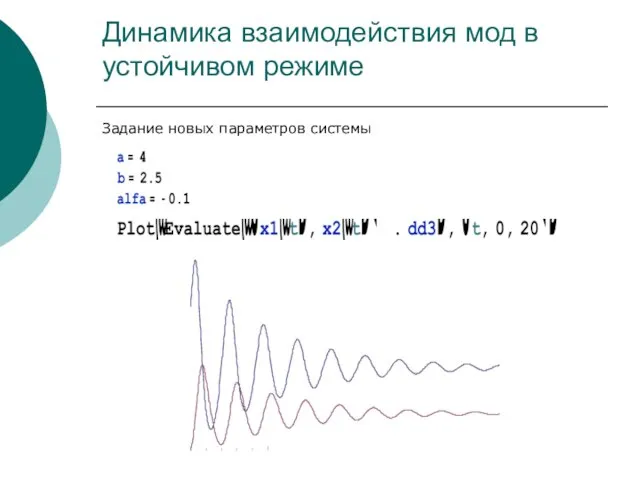
Динамика взаимодействия мод в устойчивом режиме
Задание новых параметров системы

Фазовый портрет системы в устойчивом режиме
Наблюдается устойчивый фокус

Дифуравнения, обеспечивающие устойчивое развитие системы

Фазовый портрет системы в режиме устойчивого взаимодействия мод
Наблюдается быстрая эволюция систмы к устойчивому состоянию с устойчивым фокусом.

Взаимодействие приводит к переходу системы в устойчивое состояние с изменением энергии мод

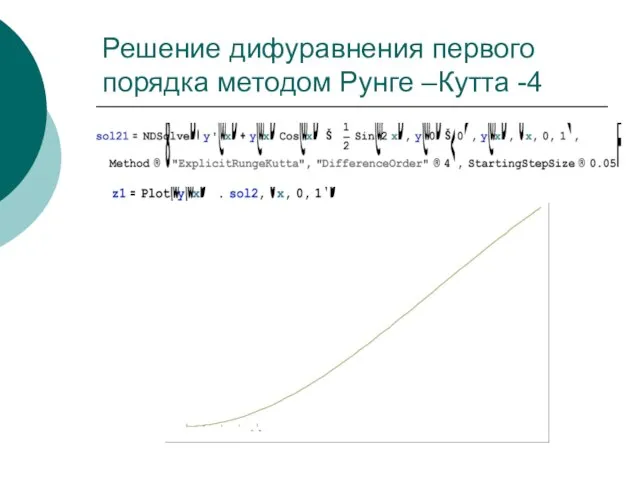
Решение дифуравнения первого порядка методом Рунге –Кутта -4

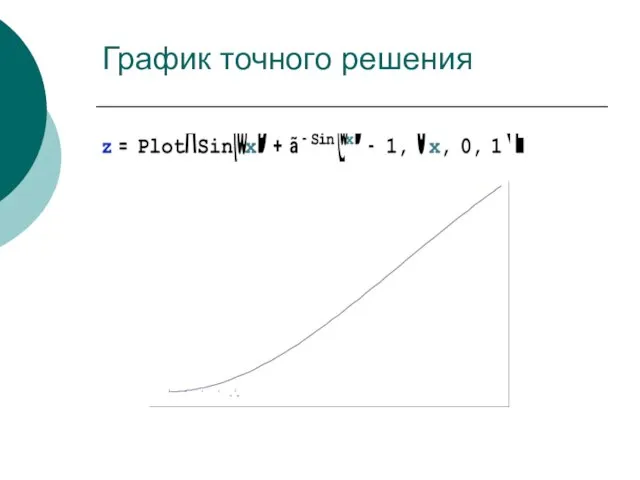
График точного решения

Решение неоднородного дифуравнения второго порядка
Задача 4

Аппроксимация эмпирических данных в пакете Maple 12
> X := [1, 2, 3, 4, 5, 6, 7, 8, 9];
X := [1, 2, 3, 4, 5, 6, 7, 8, 9]
> Y := [.25, .111, 0.71e-1, 0.53e-1, 0.42e-1, 0.39e-1, 0.33e-1, 0.31e-1, 0.29e-1];
Y := [0.25, 0.111, 0.071, 0.053, 0.042, 0.039, 0.033, 0.031, 0.029]
> with(CurveFitting);[BSpline, BSplineCurve, Interactive, InteractiveChangeSlider, LeastSquares, PolynomialInterpolation, RationalInterpolation, Spline, ThieleInterpolation]> af1 := proc (v) options operator, arrow; LeastSquares(X, Y, v, curve = a*v^2+b*v+c) end proc; / 2 \ af1 := v -> CurveFitting:-LeastSquares\X, Y, v, curve = a v + b v + c/> LeastSquares(X, Y, v, curve = a*v^2+b*v+c); 2 0.2849047619 - 0.0805147186147184140 v + 0.00602813852813851009 v > af2 := proc (v) options operator, arrow; LeastSquares(X, Y, v, curve = a*v^3+b*v^2+c*v+d) end proc; / 3 2 \af2 := v -> CurveFitting:-LeastSquares\X, Y, v, curve = a v + b v + c v + d/> LeastSquares(X, Y, v, curve = a*v^3+b*v^2+c*v+d); 3 0.3912380952 - 0.182336940836941020 v - 0.00161111111111111372 v 2 + 0.0301948051948052361 v > af3 := proc (v) options operator, arrow; LeastSquares(X, Y, v, curve = a*v^4+b*v^3+c*v^2+d*v+e) end proc; / af3 := v -> CurveFitting:-LeastSquares\X, Y, v, 4 3 2 \ curve = a v + b v + c v + d v + e/

Приближение данных различными аналитическими функциями
af4 := proc (v) options operator, arrow; LeastSquares(X, Y, v, curve = a/v+b) end proc; / a \ af4 := v -> CurveFitting:-LeastSquares|X, Y, v, curve = - + b| \ v /> LeastSquares(X, Y, v, curve = a/v+b);
plotdata := pointplot(data);
> paf1 := plot(af1(h), h = 0 .. 10, color = red);
> paf2 := plot(af2(h), h = 0 .. 10, color = blue);
> paf3 := plot(af3(h), h = 0 .. 10, color = green);
> paf4 := plot(af4(h), h = 0 .. 10, af4 = 0 .. .5, color = coral);> with(plots);

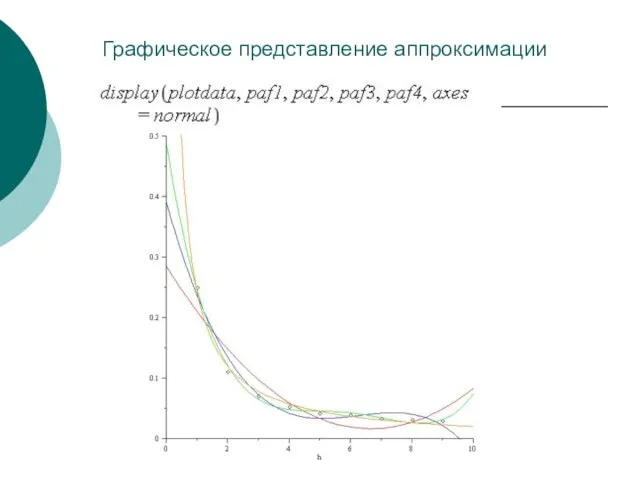
Графическое представление аппроксимации

Решение дифуравнения первого порядка методом РК4 в пакете Maple 12

Шаг 0.05
> pf := plot(phi(x), x = 1 .. 2, color = blue);
> a1 := odeplot(de1, 1 .. 2, style = point, symbolsize = 20);
> a2 := odeplot(de2, 1 .. 2, style = point, symbolsize = 20);
> a3 := odeplot(de3, 1 .. 2, style = point, symbolsize = 20);
> display(pf, a1);

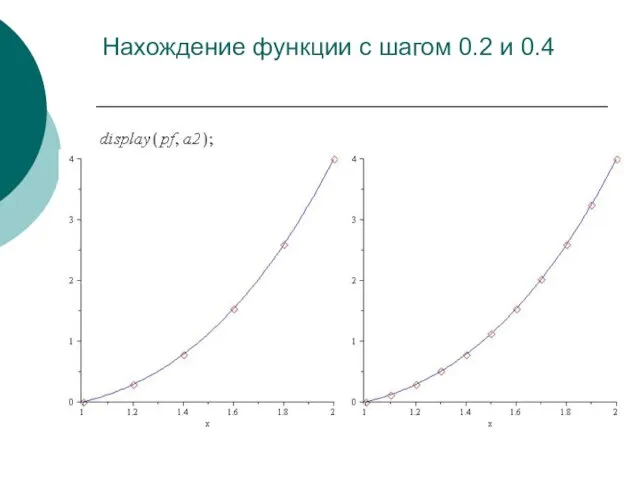
Нахождение функции с шагом 0.2 и 0.4

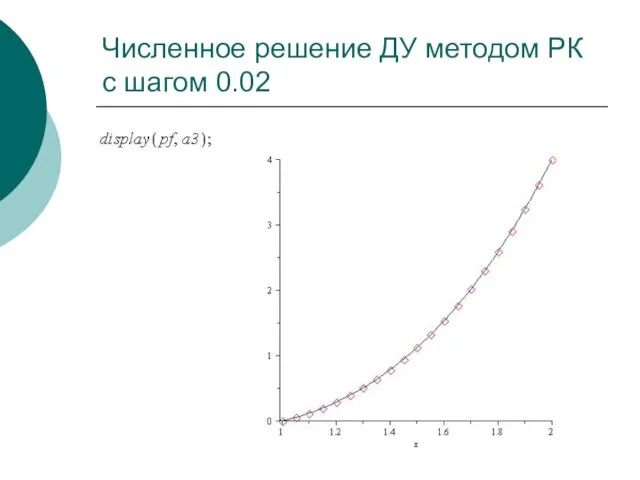
Численное решение ДУ методом РК с шагом 0.02

Решение ДУ второго порядка методом РК4 сведением к системе двух уравнений первого порядка
> ode := x^2*(diff(y(x), `$`(x, 2)))-6*y(x);
> ic := y(1) = 1, (D(y))(1) = 3;
> c := convertsys({ode}, [ic], y(x), x, p);
p1 := proc (x) options operator, arrow; y(x) end proc; p2 := proc (x) options operator, arrow; (D(y))(x) end proc;
> sys := diff(p1(x), x) = p2(x), diff(p2(x), x) = 6*p1(x)/x^2;
> icp := p1(1) = 1, p2(1) = 3;
> x1[0] := a; for i from 0 to n1-1 do x1[i+1] := x1[i]+h1 end do;

Решение неоднородного ДУ второго порядка методом РК4
f := proc (x) options operator, arrow; exp(-3*x)*cos(x) end proc;
> a1 := 2; a2 := 0; a := (1/2)*Pi;
> ode := diff(y(x), `$`(x, 2))+a1*(diff(y(x), x))+a2*y(x);
> ic := y(a) = 0, (D(y))(a) = 0;

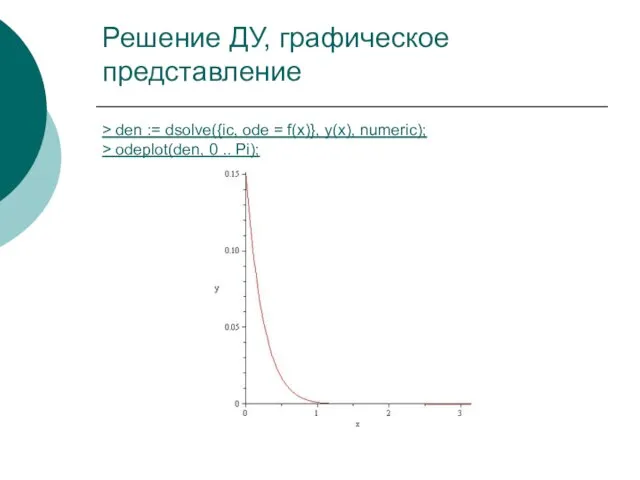
Решение ДУ, графическое представление
> den := dsolve({ic, ode = f(x)}, y(x), numeric);
> odeplot(den, 0 .. Pi);

Решение системы ДУ первого порядка. Режимы эволюции мод
restart;> ode1 := diff(x1(t), t) = (a-b*x2(t))*x1(t)-alpha*x1(t)^2;
> ode2 := diff(x2(t), t) = (-c+d*x1(t))*x2(t)-alpha*x2(t)^2;
> a := 4; b := 3.5; c := 2; d := 1; alpha := .2;
> ic := x1(0) = 3, x2(0) = 1;
> de := dsolve({ic, ode1, ode2}, {x1(t), x2(t)}, numeric);> with(plots);

Фазовый портрет системы