Содержание
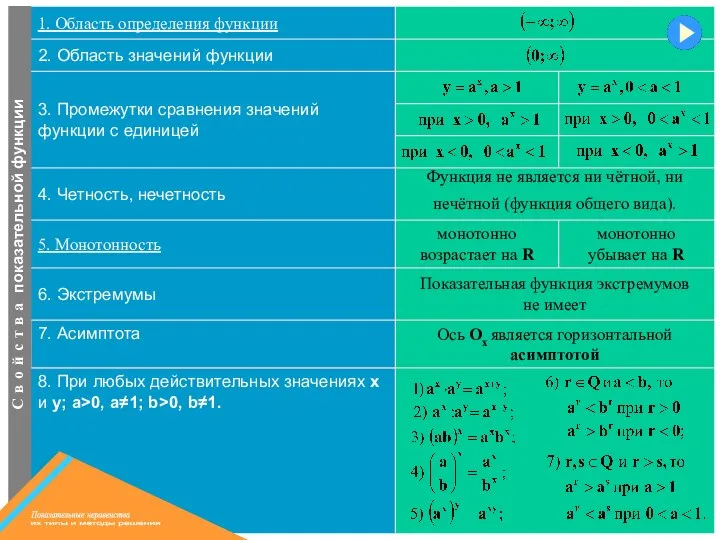
- 2. монотонно убывает на R Ось Ох является горизонтальной асимптотой монотонно возрастает на R 8. При любых
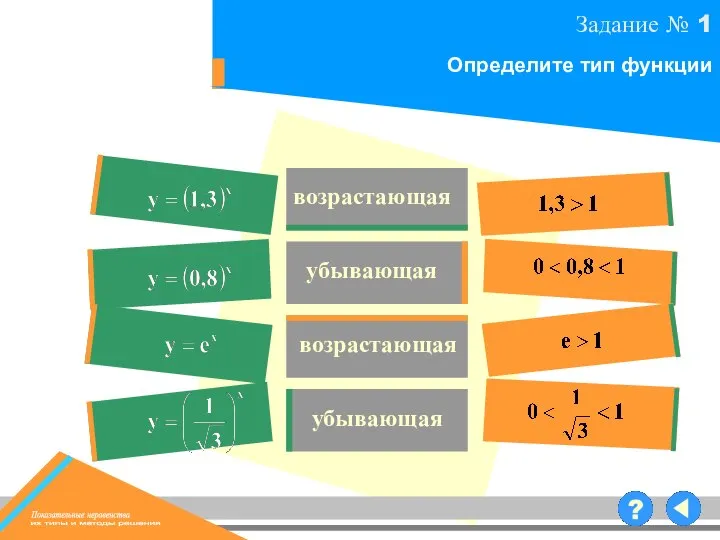
- 3. возрастающая убывающая возрастающая убывающая
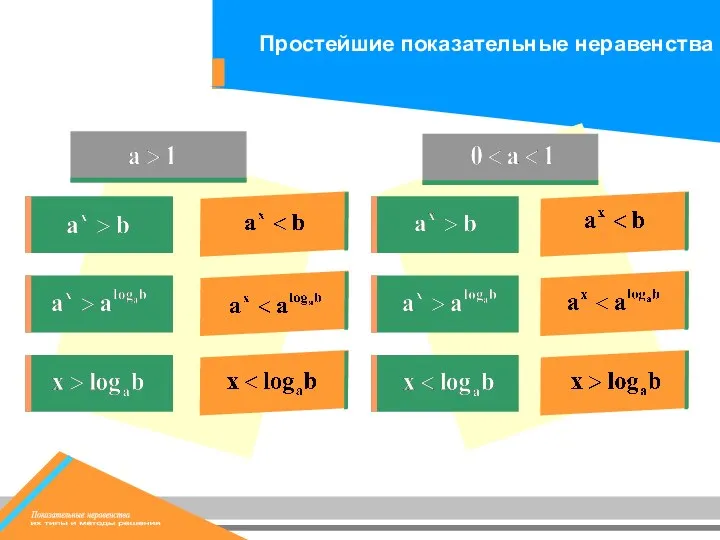
- 4. Пусть а – данное положительное, не равное единице число и b – данное действительное число. Тогда
- 5. Решением неравенства с неизвестным х называют число х0, при подстановке которого в неравенство получается верное числовое
- 6. Решить неравенство – значит, найти все его решения или показать, что их нет.
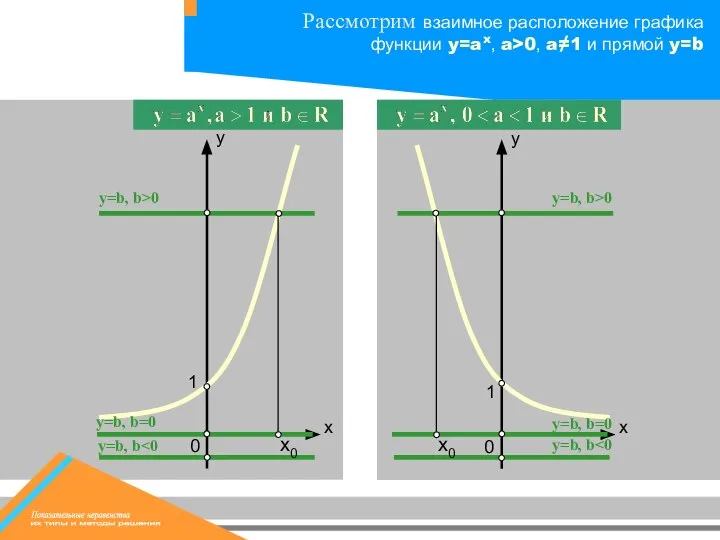
- 7. y=b, b y=b, b y=b, b=0 y=b, b=0 y=b, b>0 y=b, b>0 0 1 0 1
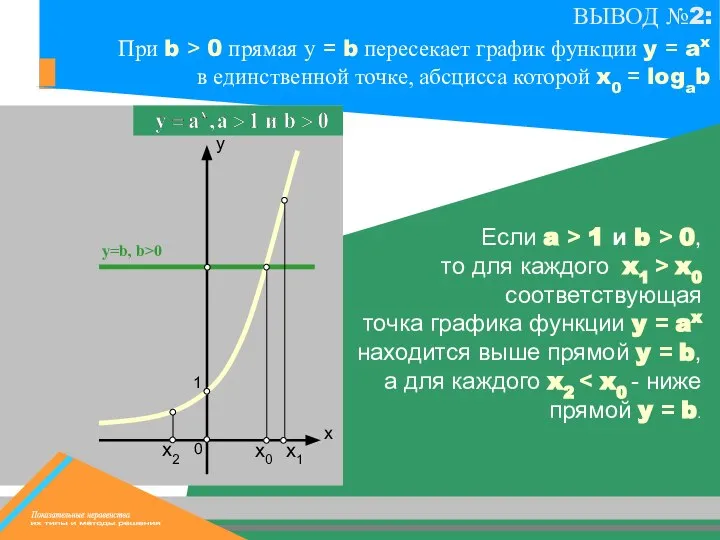
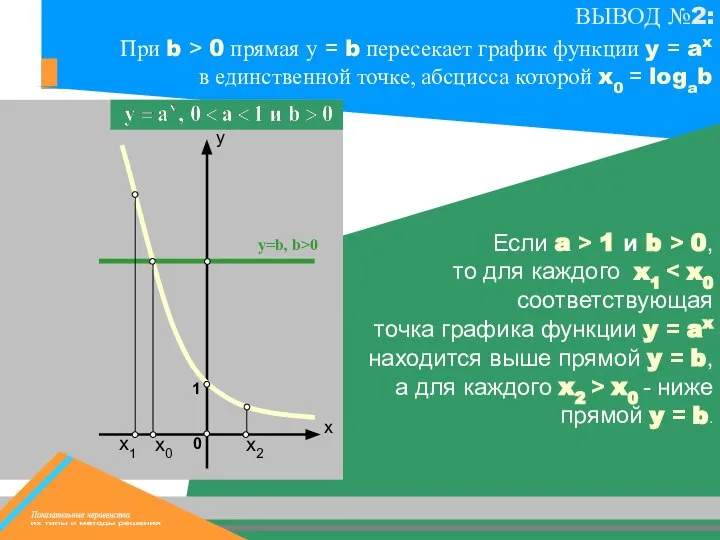
- 9. х0 х1 y=b, b>0 1 Если a > 1 и b > 0, то для каждого
- 10. х0 х1 y=b, b>0 х2 Если a > 1 и b > 0, то для каждого
- 12. возрастает на всей области определения, Решение:
- 13. Решение: убывает на всей области определения,
- 14. Решение: возрастает на всей области определения,
- 15. возрастает на всей области определения,
- 16. возрастает на всей области определения
- 17. возрастает на всей области определения
- 18. Вернёмся к переменной х возрастает при всех х из области определения
- 19. возрастает на всей области определения
- 20. убывает на всей области определения
- 21. Вернёмся к переменной х убывает на всей области определения
- 22. Вернёмся к переменной х возрастает на всей области определения
- 23. Решим каждое утверждение совокупности отдельно.
- 25. Скачать презентацию
















 Параллельное и последовательное соединения
Параллельное и последовательное соединения 1665470218901_Лекция Бернулли-1
1665470218901_Лекция Бернулли-1 Математический анализ. Производная и первообразная
Математический анализ. Производная и первообразная Доли. Математический диктант
Доли. Математический диктант Аксиома параллельных прямых
Аксиома параллельных прямых Внесение множителя под знак корня. Вынесение множителя из-под знака корня
Внесение множителя под знак корня. Вынесение множителя из-под знака корня Математика без границ. Конкурс
Математика без границ. Конкурс Координатная плоскость
Координатная плоскость Множественный регрессионный анализ
Множественный регрессионный анализ Игра Что? Где? Почему?
Игра Что? Где? Почему? Приемы быстрого счёта в математике
Приемы быстрого счёта в математике Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Гистограммы. Представление статистических данных в графическом виде
Гистограммы. Представление статистических данных в графическом виде Природа России в цифрах и загадках
Природа России в цифрах и загадках Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Прогрессия. Анзац
Прогрессия. Анзац Случаи вычитания 12 -
Случаи вычитания 12 - Движения. 9-й класс
Движения. 9-й класс Решение задач на тему Энергосбережение
Решение задач на тему Энергосбережение Решение уравнений и неравенств
Решение уравнений и неравенств Решение задач по теме Площадь параллелограмма, треугольника, трапеции
Решение задач по теме Площадь параллелограмма, треугольника, трапеции Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8
Действия с обыкновенными дробями. Подготовка к ОГЭ задания первой части 1, 3, 8 Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2 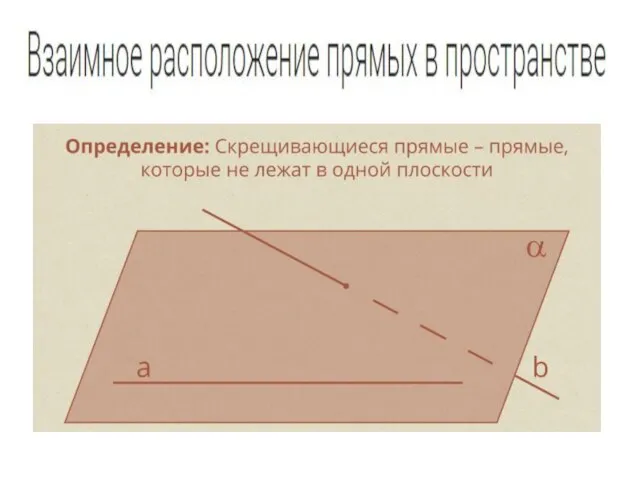 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Презентация на тему Решение задач с помощью квадратных уравнений
Презентация на тему Решение задач с помощью квадратных уравнений  Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Углы, связанные с окружностью
Углы, связанные с окружностью