- Главная
- Математика
- Полярные координаты

Содержание
Слайд 2Полярные координаты
Если на плоскости задана декартова система координат, то обычно за полярную
Полярные координаты
Если на плоскости задана декартова система координат, то обычно за полярную
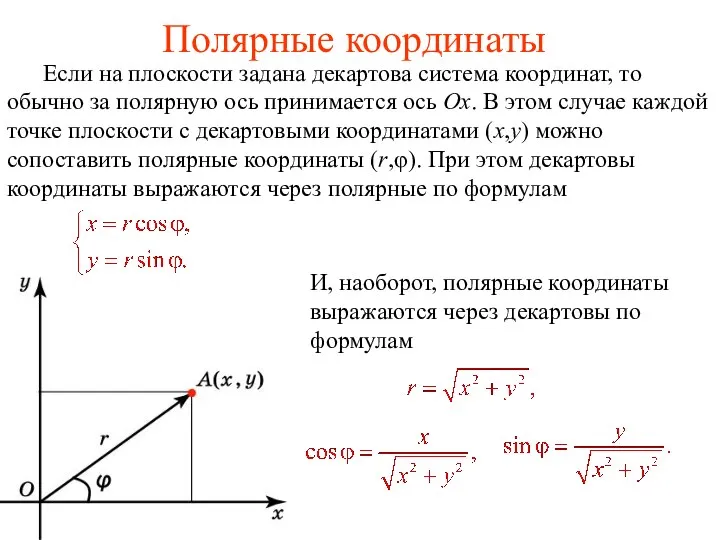
ось принимается ось Ox. В этом случае каждой точке плоскости с декартовыми координатами (x,y) можно сопоставить полярные координаты (r,φ). При этом декартовы координаты выражаются через полярные по формулам
И, наоборот, полярные координаты выражаются через декартовы по формулам
Слайд 6Упражнение 1
Постройте кривую, определяемую уравнением r = sin 3φ по 16 точкам.
Упражнение 1
Постройте кривую, определяемую уравнением r = sin 3φ по 16 точкам.

Постройте кривую, определяемую уравнением r =4- sin 5φ по 16 точкам.
Упражнение 2
Упражнение 3
Постройте кривую, определяемую уравнением
по 16 точкам.
- Предыдущая
Космология. История возникновения ВселеннойСледующая -
Источники финансирования ОБС

 Сумма n первых членов геометрической прогрессии
Сумма n первых членов геометрической прогрессии Математика и я
Математика и я Случайные погрешности
Случайные погрешности Презентация на тему Принцесса математики Софья Ковалевская
Презентация на тему Принцесса математики Софья Ковалевская  Окружность. Проверочная работа
Окружность. Проверочная работа Метод удвоения медианы
Метод удвоения медианы Физический смысл производной
Физический смысл производной Приближенные решения уравнений
Приближенные решения уравнений Решение заданий № 21 II части ГИА-2014
Решение заданий № 21 II части ГИА-2014 Измерение массы (для детей 6 лет)
Измерение массы (для детей 6 лет) Объемы тел вращения
Объемы тел вращения Прямая. Плоскость
Прямая. Плоскость Свойства умножения
Свойства умножения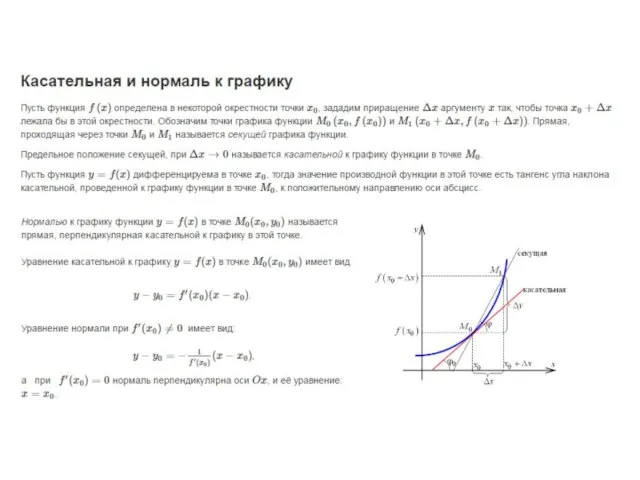 Касательная и нормаль к графику
Касательная и нормаль к графику Решение задач на определение часовых поясов и часовых зон России
Решение задач на определение часовых поясов и часовых зон России Математический анализ. Лекция 1
Математический анализ. Лекция 1 Параллельные прямые. Свойства и признаки параллельных прямых
Параллельные прямые. Свойства и признаки параллельных прямых Преобразование графиков квадратичной функции. 8 класс
Преобразование графиков квадратичной функции. 8 класс Презентация на тему Цилиндр 11 класс
Презентация на тему Цилиндр 11 класс  Математический язык
Математический язык Algebriskas nevienādības
Algebriskas nevienādības Симметрия в искусстве
Симметрия в искусстве Построение изображения цилиндра и его осевого сечения
Построение изображения цилиндра и его осевого сечения Таблица сложения
Таблица сложения Критериальная система и методика оценивания геометрических заданий 23, 24, 25 модуля Геометрия
Критериальная система и методика оценивания геометрических заданий 23, 24, 25 модуля Геометрия Замечательные точки и линии треугольника. 9 класс
Замечательные точки и линии треугольника. 9 класс Комплексные числа
Комплексные числа Теория вероятности в жизни пчел
Теория вероятности в жизни пчел