Случайные погрешности

Пример. Пусть при измерении напряжения при помощи вольтметра,
позволяющего производить измерения с дискретностью отсчета в 1 В,
были получены следующие 10 значений: 34, 36, 34, 38, 36, 33, 35, 37, 38, 34 В.
Далее запишем полученные значения в порядке возрастания (х1 < х2 < … < хk)
в таблицу и занесем в нее, сколько раз было получено каждое значение
nk (k = 1, 2, …, m).
Причем .

Из полученных значений можно вычислить среднее арифметическое:
= 35.5
Среднее значение можно получить, используя средневзвешенную сумму, так как
по своему смыслу nk является весовым множителем для каждого xk:
= 35.5
Далее вместо числа реализаций nk можно ввести относительные частоты
Fk = nk /N появления xk.
Если N будет стремиться к бесконечности, то частоты будут стремиться к
вероятностям pk появления конкретных значений дискретной случайной
величины. Заметим, что сумма всех вероятностей будет всегда равна единице
- условие нормировки

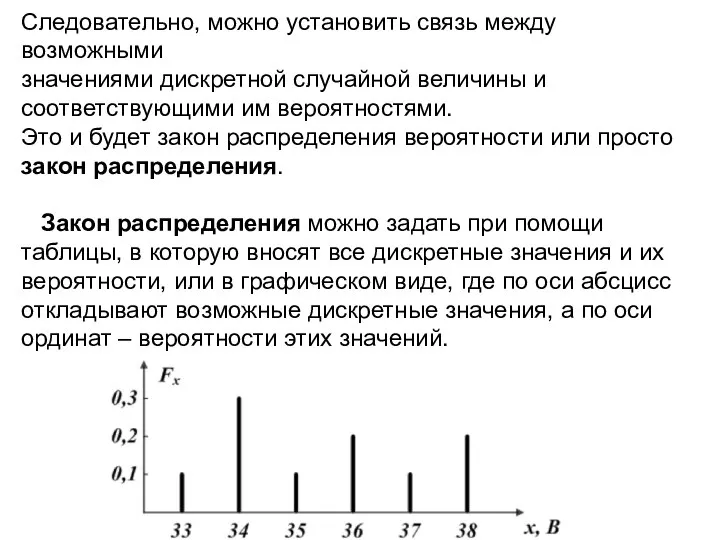
Следовательно, можно установить связь между возможными
значениями дискретной случайной величины и
соответствующими им вероятностями.
Это и будет закон распределения вероятности или просто
закон распределения.
Закон распределения можно задать при помощи таблицы, в которую вносят все дискретные значения и их вероятности, или в графическом виде, где по оси абсцисс откладывают возможные дискретные значения, а по оси ординат – вероятности этих значений.

Кроме закона распределения для характеристики дискретных случайных величин используются такие параметры, как математическое ожидание и дисперсия.
В общем случае под математическим ожиданием случайной величины понимают сумму произведений всех ее возможных значений на вероятность этих значений:
- совпадает с средним.

Дисперсия – математическое ожидание квадрата
отклонения случайной величины от её
математического ожидания
Дисперсия имеет размерность квадрата измеряемой
случайной величины, поэтому вводят понятие среднего
квадратического отклонения (СКО):
СКО будет иметь размерность самой измеряемой величины.
Характеризуют степень разброса случайной величины от среднего
значения

4.1.2. Непрерывные случайные величины
Функция распределения вероятности слуайной величины
(интегральный закон распределения)
- вероятность того, величина принимает значение от - до х.
значения которых не отделены друг от друга и непрерывно заполняют некоторый
промежуток
Вот ее общие свойства:
1. Функция распределения F(x) является неубывающей функцией: т.е. при x1 < 2 F(x1) < F(x2).
2. При x = - ∞ F(- ∞) = 0: на минус бесконечности функция распределения равна нулю.
3. При x = + ∞ F(+∞) = 1: на плюс бесконечности функция распределения равна единице.

нормировка
Математическое ожидание непрерывной случайной величины:
Дисперсия,
среднее квадратическое отклонение
Для непрерывной случайной величины с непрерывной и дифференцируемой функцией распределения вероятности F(x) можно использовать дифференциальный закон распределения вероятностей (или плотность распределения вероятности):
Эта функция всегда неотрицательна и подчинена условию нормирования:

В метрологии существует много законов распределения. Чаще всего в измерительной практике применяются два: равномерный и нормальный (распределение Гаусса).

4.1.3. Равномерный закон распределения
Функция распределения и
Плотность распределения
Математическое ожидание
M(X) = (x1+x2)/2
Дисперсия
D(X) = (b – a)2/2
При равномерном законе возможные значения непрерывной случайной величины находятся в пределах некоторого конечного интервала и имеют одну и ту же плотность вероятности

Примеры равномерно распределенных случайных величин.
Автомобиль подъезжает к перекрестку, регулируемому светофором, в некоторый момент времени. На светофоре – красный сигнал. Полное время «горения» красного сигнала – 30 секунд. Время Т, в течение которого водителю автомобиля придется ждать зеленого сигнала светофора, представляет собой случайную величину, равномерно распределенную на отрезке [0, 30].
встречается в измерительной практике при округлении отсчётов измерительных приборов до целых делений шкал
Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину, распределенную с постоянной плотностью между двумя соседними делениями.

4.1.4.. Нормальный закон распределения
(гауссовское распределение)
Аксиомы:
Аксиома симметрии: одинаковые по величине и разные
по знаку отклонения величины от среднего значения
встречаются одинаково часто;
2) Аксиома монотонного убывания плотности
Вероятности: большие отклонения величины встречаются реже.
Широко применяется в задачах практики
- вероятность того, что случайная величина лежит в интервале (х1, х2)
Чем больше дисперсия (разброс,
отклонение от среднего),
тем ниже и шире кривая
Формула нормального закона распределения имеет следующий вид:
где x - среднее значение; σ- среднее квадратическое отклонение (СКО).

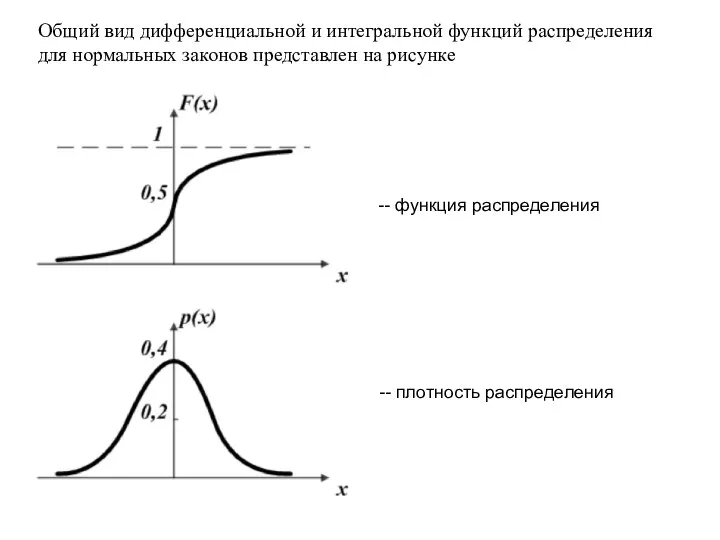
Общий вид дифференциальной и интегральной функций распределения для нормальных законов представлен на рисунке
-- функция распределения
-- плотность распределения

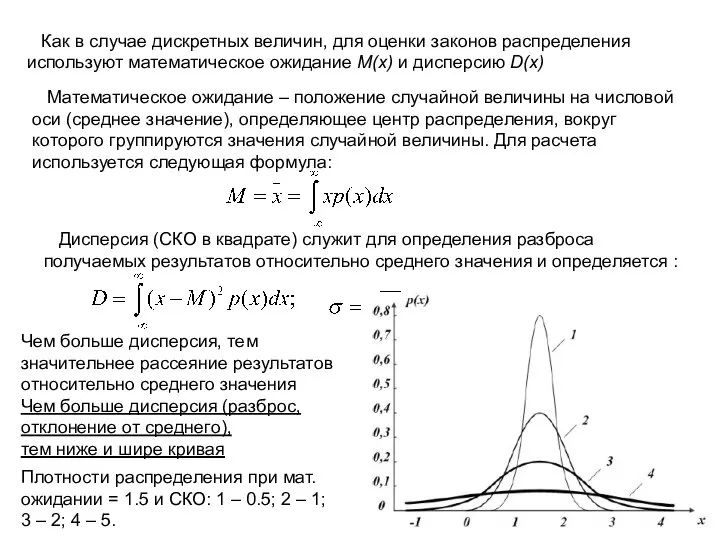
Как в случае дискретных величин, для оценки законов распределения используют математическое ожидание М(х) и дисперсию D(x)
Математическое ожидание – положение случайной величины на числовой оси (среднее значение), определяющее центр распределения, вокруг которого группируются значения случайной величины. Для расчета используется следующая формула:
Дисперсия (СКО в квадрате) служит для определения разброса получаемых результатов относительно среднего значения и определяется :
Чем больше дисперсия, тем значительнее рассеяние результатов относительно среднего значения
Чем больше дисперсия (разброс,
отклонение от среднего),
тем ниже и шире кривая
Плотности распределения при мат.
ожидании = 1.5 и СКО: 1 – 0.5; 2 – 1;
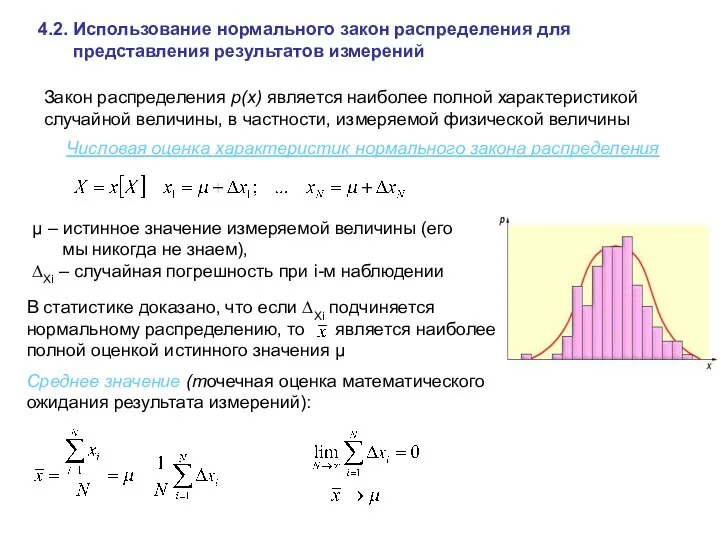
3 – 2; 4 – 5.

На практике все результаты измерений являются дискретными величинами, т. е. из всей генеральной совокупности (всех возможных значений) мы при измерении получаем некоторый ряд значений, который называется выборкой.
Полученная выборка должна быть репрезентативной, т. е. достаточно хорошо представлять пропорции генеральной совокупности.
Далее встает задача нахождения точечных оценок, характеризующих распределение величин, входящих в данную выборку. Эти оценки должны быть:
***состоятельными (при увеличении объема выборки должны стремиться к истинному значению величины),
***несмещенными (математическое ожидание оценки равно оцениваемой числовой характеристике) и
***эффективными (иметь как можно меньшую дисперсию).

4.2. Использование нормального закон распределения для
представления результатов измерений
Закон распределения р(x) является наиболее полной характеристикой
случайной величины, в частности, измеряемой физической величины
Среднее значение (точечная оценка математического
ожидания результата измерений):
Числовая оценка характеристик нормального закона распределения
μ – истинное значение измеряемой величины (его
мы никогда не знаем),
∆Xi – случайная погрешность при i-м наблюдении
В статистике доказано, что если ∆Xi подчиняется
нормальному распределению, то является наиболее
полной оценкой истинного значения μ

- характеризует разброс результатов наблюдений относительно
Среднее квадратическое
отклонение наблюдений
(СКО):
Среднее квадратическое
отклонение результата измерений
(СКО среднего):
- характеризует отклонение относительно истинного значения μ
Полученные оценки математического ожидания и среднего квадратического отклонения являются случайными величинами. Это проявляется в том, при повторении несколько раз серий из n наблюдений каждый раз будут получаться различные оценки и Sx. Рассеяние этих оценок принято оценивать СКО среднего:

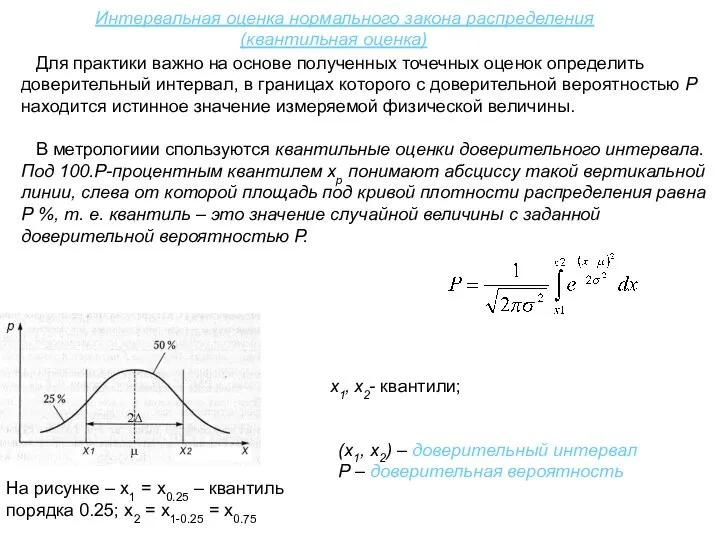
Интервальная оценка нормального закона распределения
(квантильная оценка)
x1, x2- квантили;
(x1, x2) – доверительный интервал
P – доверительная вероятность
На рисунке – х1 = х0.25 – квантиль
порядка 0.25; х2 = х1-0.25 = х0.75
Для практики важно на основе полученных точечных оценок определить доверительный интервал, в границах которого с доверительной вероятностью Р находится истинное значение измеряемой физической величины.
В метрологиии спользуются квантильные оценки доверительного интервала. Под 100.Р-процентным квантилем xp понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р %, т. е. квантиль – это значение случайной величины с заданной доверительной вероятностью Р.

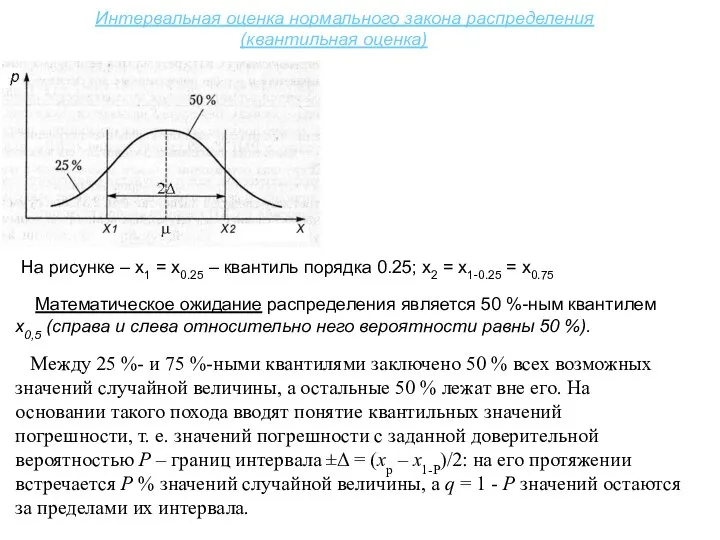
Интервальная оценка нормального закона распределения
(квантильная оценка)
На рисунке – х1 = х0.25 – квантиль порядка 0.25; х2 = х1-0.25 = х0.75
Mатематическое ожидание распределения является 50 %-ным квантилем x0,5 (справа и слева относительно него вероятности равны 50 %).
Между 25 %- и 75 %-ными квантилями заключено 50 % всех возможных значений случайной величины, а остальные 50 % лежат вне его. На основании такого похода вводят понятие квантильных значений погрешности, т. е. значений погрешности с заданной доверительной вероятностью Р – границ интервала ±Δ = (xp – x1-P)/2: на его протяжении встречается Р % значений случайной величины, а q = 1 - Р значений остаются за пределами их интервала.

Интервальная оценка нормального закона распределения
(квантильная оценка)
2. Результат измерений: среднее арифметическое с вероятностью Р
отклоняется от истинного значения не более чем на Δ
Действия 1: провести N измерений, вычислить среднее арифметическое
(принять за μ), вычислить СКО среднего арифметического (принять за σ),
задаться доверительным интервалом Δ, рассчитать доверительную
вероятность Р

!!! Нормальный закон распределения – для выборки с большим количеством случайных величин. N > 30
******************************************************************************
Стьюдент – псевдоним У.С. Госсета (1876-1937) – химика, работавшего в одной из пивоваренных фирм Великобритании. Он самостоятельно разработал статистику малых выборок. Поскольку в современной технике чаще всего исследуются небольшие по объему выборки (менее 30), то работа Стьюдента имеет большое практическое значение.
При малом количестве наблюдений (n < 30) пользуются не нормальным законом распределения, а распределением Стьюдента. Оно описывает плотность распределения отношением:

Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале от – tP до + tP можно рассчитать так:
где k – число степеней свободы (n – 1). Коэффициенты Стьюдента табулированы. Поэтому с помощью распределения Стьюдента можно найти вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает следующей величины:
- случайная погрешность

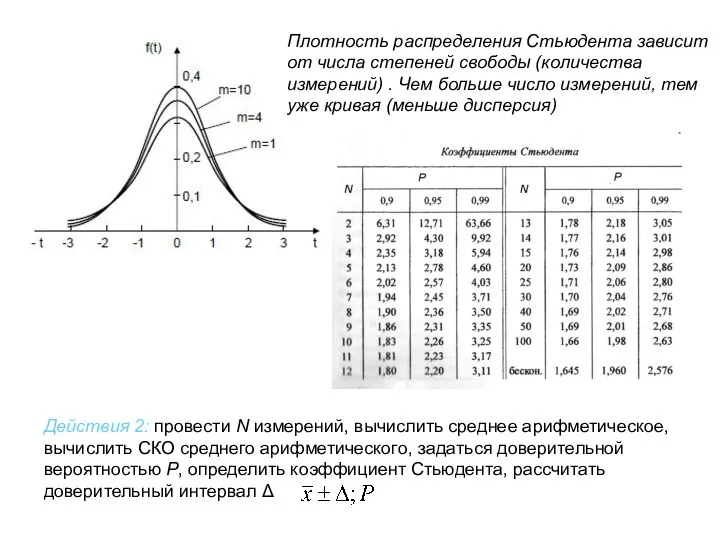
Плотность распределения Стьюдента зависит от числа степеней свободы (количества измерений) . Чем больше число измерений, тем уже кривая (меньше дисперсия)
Действия 2: провести N измерений, вычислить среднее арифметическое,
вычислить СКО среднего арифметического, задаться доверительной
вероятностью Р, определить коэффициент Стьюдента, рассчитать
доверительный интервал Δ

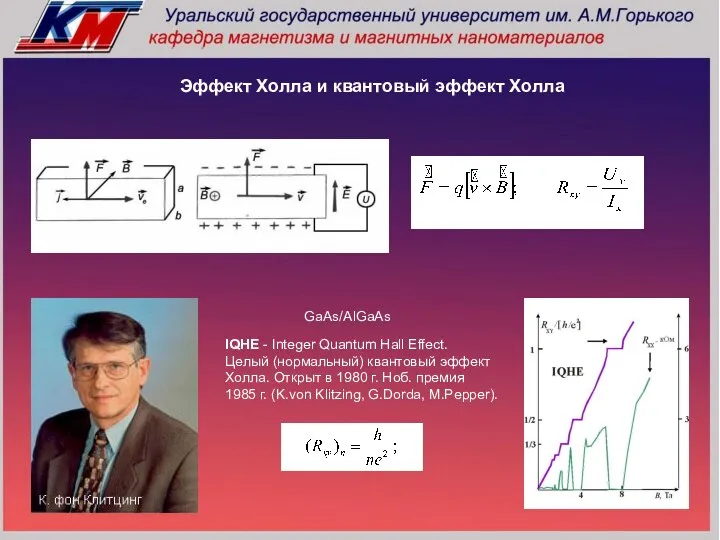
IQHE - Integer Quantum Hall Effect.
Целый (нормальный) квантовый эффект
Холла. Открыт в 1980 г. Ноб. премия
1985 г. (K.von Klitzing, G.Dorda, M.Pepper).
Эффект Холла и квантовый эффект Холла
GaAs/AlGaAs