Симметрия в искусстве

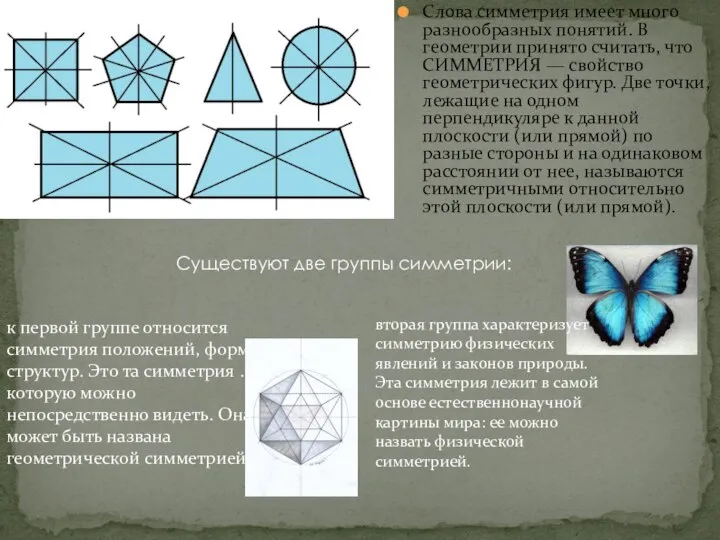
Слова симметрия имеет много разнообразных понятий. В геометрии принято считать, что СИММЕТРИЯ — свойство геометрических фигур. Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой).
а
Существуют две группы симметрии:
к первой группе относится симметрия положений, форм, структур. Это та симметрия .которую можно непосредственно видеть. Она может быть названа геометрической симметрией;
вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией.

Герман Вейл(известный математик прошлого столетия) говорил: «Симметрия…есть идея,с помощью которой человек веками пытался объяснить и создать порядок,красоту и совершенство».

Виды симметрии.

Принцип симметрии охватывает все новые области. Из области кристалл лографии, физики твердого тела он вошел в область химии, в область молекулярных процессов и в физику атома. Нет сомнения, что его проявления мы найдем в еще более далеком от окружающих нас комплексов мире электрона, и ему подчинены будут явления квантов», – это слова академика В. И. Вернадского, занимавшегося изучением принципов симметрии в неживой природе.
Симметрия, проявляясь в самых различных объектах материального мира, несомненно, отражает наиболее общие, наиболее фундаментальные его свойства.
Поэтому исследование симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.
Можно увидеть, что это кажущаяся простота уведет нас далеко в мир науки и техники и позволит время от времени подвергать испытанию способности нашего мозга (так как именно он запрограммирован на симметрию)
Заключение.