Содержание
- 2. Цели урока Знать: определение вектора в пространстве и связанные с ним понятия; равенство векторов. Уметь: решать
- 3. Понятие вектора появилось в 19 веке в работах математиков Г. Грассмана У. Гамильтона
- 4. Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши.
- 5. Задание Записать все термины по теме «Векторы на плоскости». Вектор Нулевой вектор Длина вектора Коллинеарные векторы
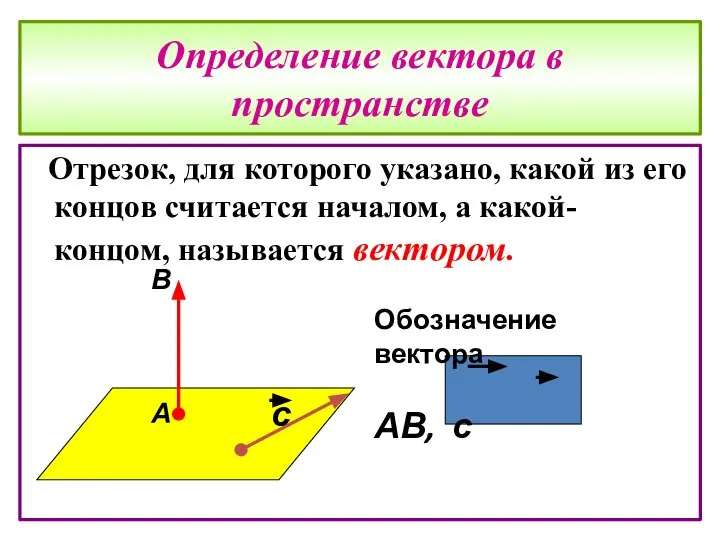
- 6. Определение вектора в пространстве Отрезок, для которого указано, какой из его концов считается началом, а какой-
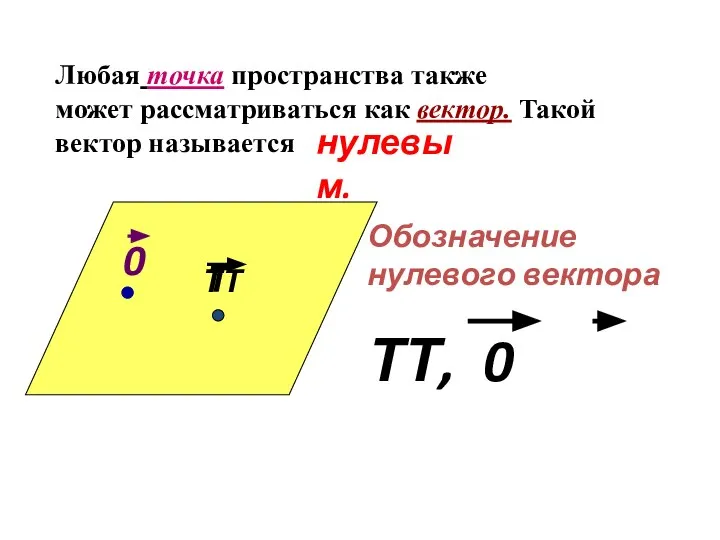
- 7. Т Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым.
- 8. Длина ненулевого вектора Длиной вектора АВ называется длина отрезка АВ. Длина вектора АВ (вектора а) обозначается
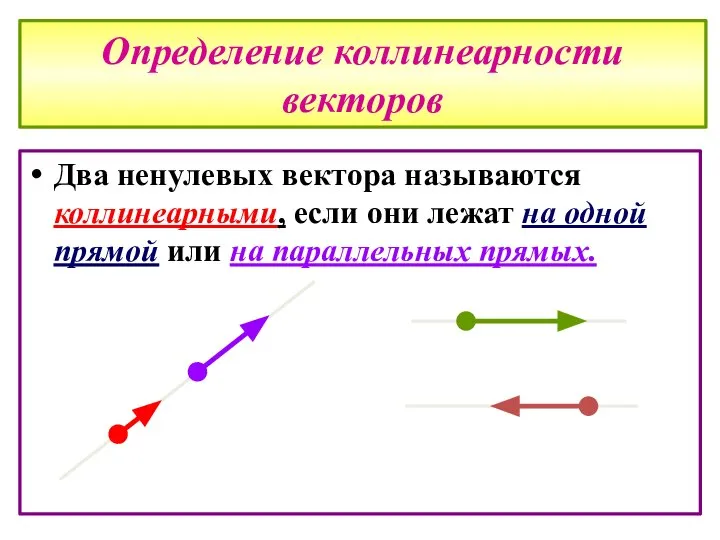
- 9. Определение коллинеарности векторов Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на
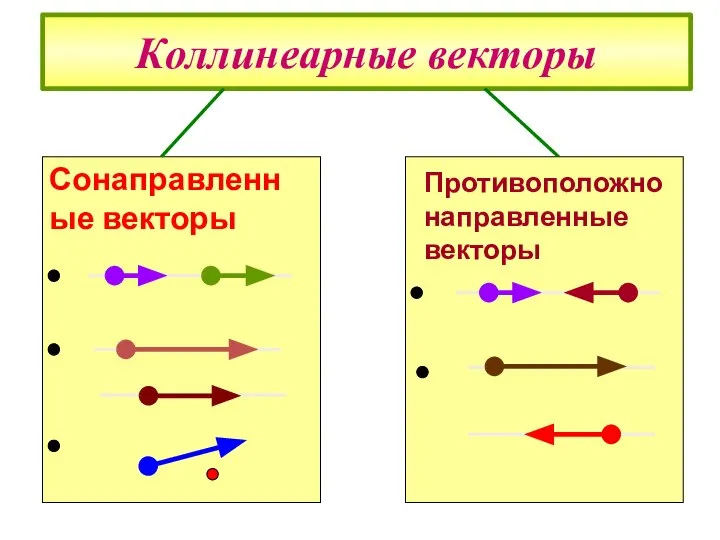
- 10. Коллинеарные векторы Противоположно направленные векторы Сонаправленные векторы
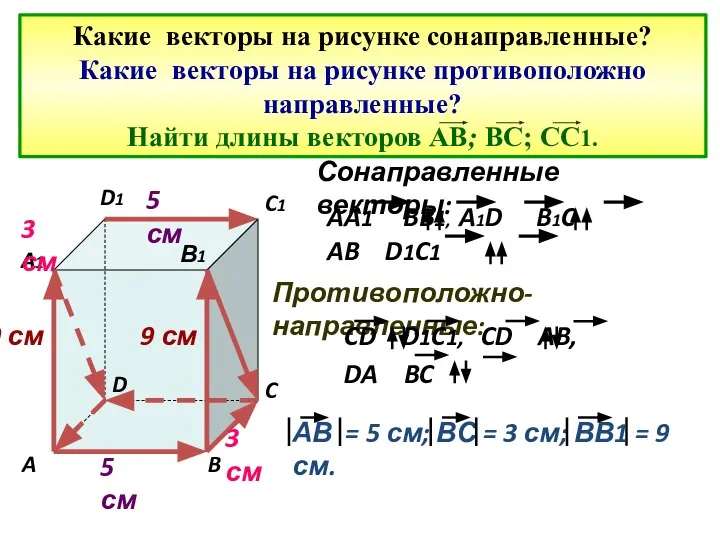
- 11. Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ; ВС;
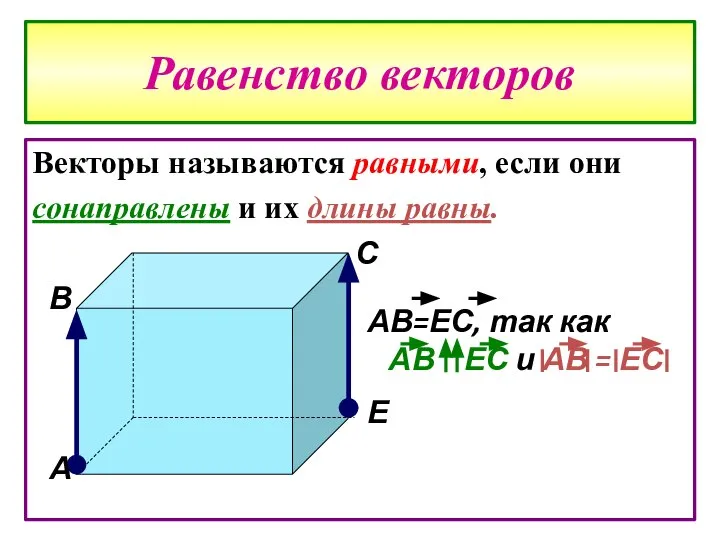
- 12. Равенство векторов Векторы называются равными, если они сонаправлены и их длины равны. А В С Е
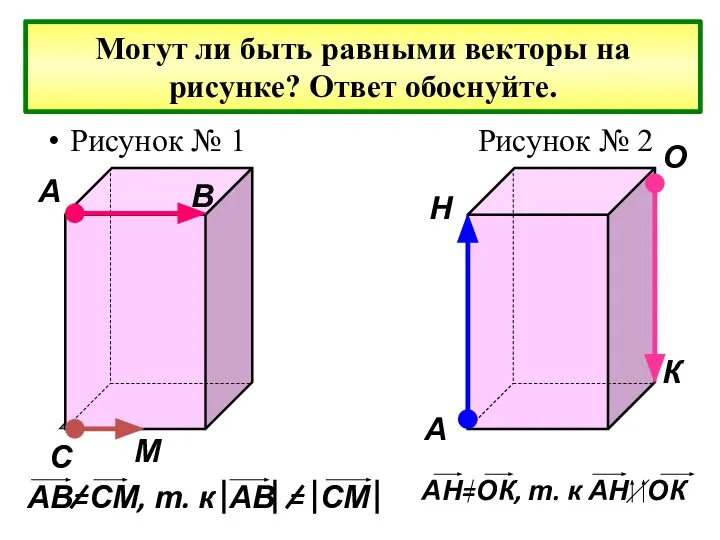
- 13. Могут ли быть равными векторы на рисунке? Ответ обоснуйте. Рисунок № 1 Рисунок № 2 А
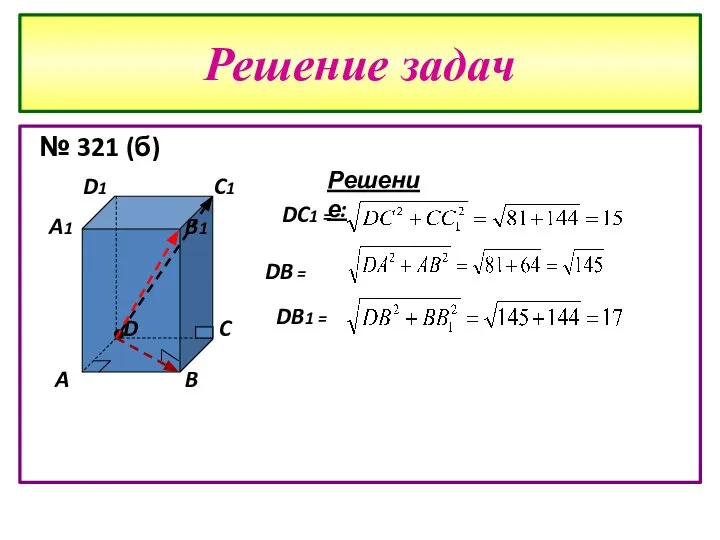
- 14. Решение задач № 321 (б) A B C D A1 B1 C1 D1 Решение: DC1 =
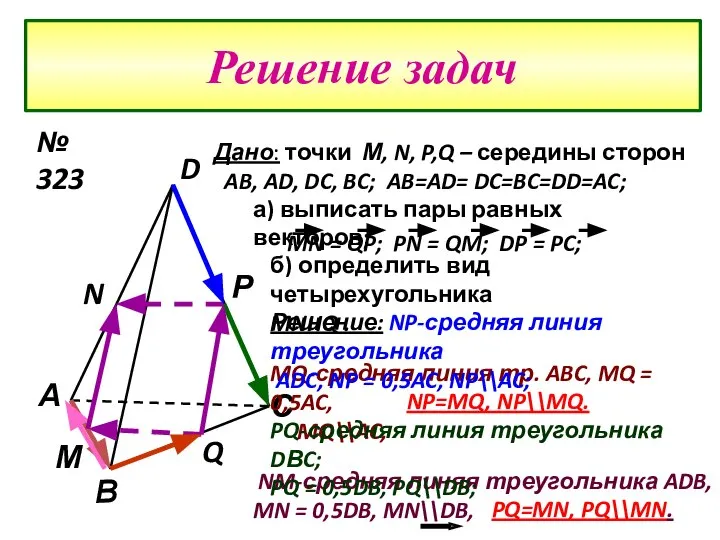
- 15. Решение задач А D С В М Р N Q Дано: точки М, N, P,Q –
- 17. Скачать презентацию





 Квадратный корень
Квадратный корень Решение примеров
Решение примеров Многогранник с двумя основаниями
Многогранник с двумя основаниями Площадь окружности
Площадь окружности Геометрические фигуры
Геометрические фигуры Виды треугольников. 5 класс
Виды треугольников. 5 класс Применение подобия к доказательству теорем и решению задач. Урок 40
Применение подобия к доказательству теорем и решению задач. Урок 40 Первообразная функции
Первообразная функции Многоугольники
Многоугольники Умножение одночлена на многочлен. 7 класс
Умножение одночлена на многочлен. 7 класс Смежные и вертикальные углы
Смежные и вертикальные углы Общие методы решения уравнений
Общие методы решения уравнений Пустое множество
Пустое множество Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Параллельный перенос
Параллельный перенос Загадки о цифрах
Загадки о цифрах Комбинаторная задача с шарами
Комбинаторная задача с шарами Основное свойство алгебраической дроби
Основное свойство алгебраической дроби Площадь криволинейной трапеции
Площадь криволинейной трапеции Корень степени
Корень степени Презентация на тему Перпендикулярность прямой и плоскости
Презентация на тему Перпендикулярность прямой и плоскости  Применение производной к построению графиков функций
Применение производной к построению графиков функций Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике Умножение и деление алгебраических дробей (8 класс)
Умножение и деление алгебраических дробей (8 класс) Математические ассоциации координатная плоскость и другие термины
Математические ассоциации координатная плоскость и другие термины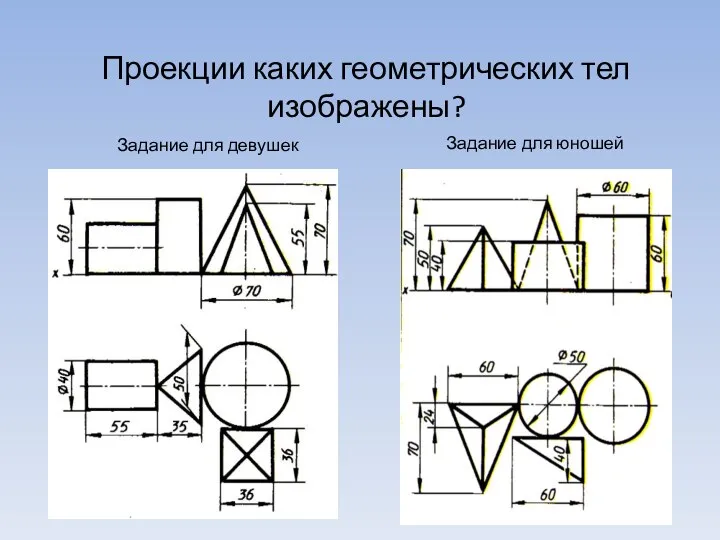 Проекции каких геометрических тел изображены?
Проекции каких геометрических тел изображены? Геометрия. Решение задач
Геометрия. Решение задач Корень степени n
Корень степени n