Содержание
- 2. где F(x) – одна из первообразных для функции f(x) Площадь криволинейной трапеции можно вычислить по формуле
- 3. Разность F(b) – F(a) называют интегралом от функции f(x) на отрезке [a;b] и обозначают: (читается: «Интеграл
- 4. f(x) - dx – a – b – знак интеграла подынтегральная функция элемент интегрирования верхний предел
- 5. Т.е. Данную формулу называют формулой Ньютона-Лейбница в честь создателей дифференциального и интегрального исчисления.
- 6. При вычислении интегралов удобно ввести обозначение: Тогда формулу Ньютона-Лейбница можно записать в виде:
- 7. Например:
- 8. Например:
- 9. Например:
- 10. Например:
- 11. Например:
- 12. Вычислите интегралы:
- 13. Вычислите интегралы:
- 14. Вычислите интегралы:
- 16. Скачать презентацию

![Разность F(b) – F(a) называют интегралом от функции f(x) на отрезке [a;b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/919086/slide-2.jpg)



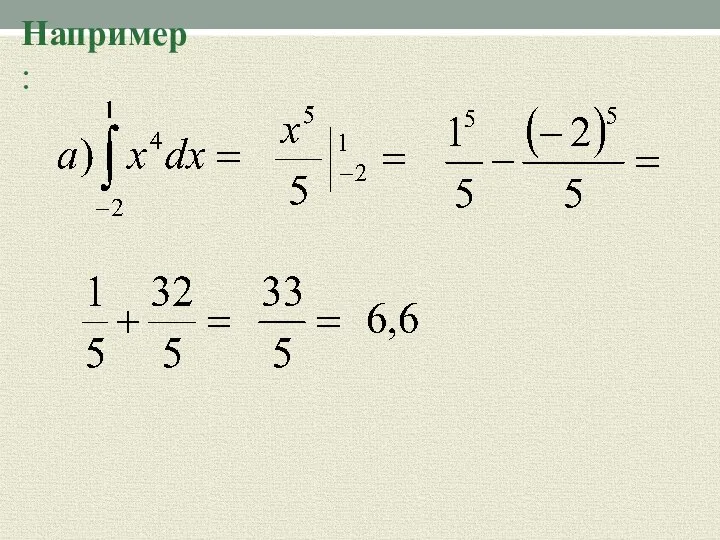
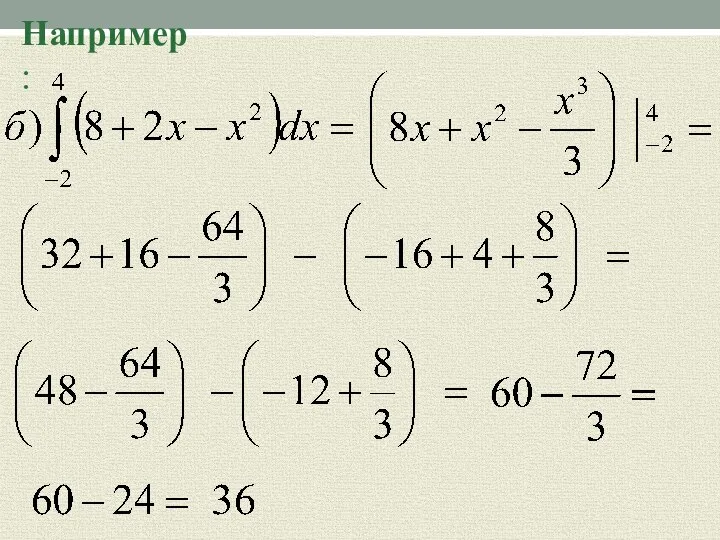






 Проектирование разноритмичных и неритмичных потоков
Проектирование разноритмичных и неритмичных потоков Первообразная. Неопределенный интеграл и его свойства
Первообразная. Неопределенный интеграл и его свойства Презентация на тему Средняя линия треугольника (8 класс)
Презентация на тему Средняя линия треугольника (8 класс)  Ось симметрии. 5 класс
Ось симметрии. 5 класс 3.3. - Квадратичная функция (1)
3.3. - Квадратичная функция (1) Презентация на тему КВАДРАТНЫЙ ТРЕХЧЛЕН
Презентация на тему КВАДРАТНЫЙ ТРЕХЧЛЕН  Множества и операции над ними
Множества и операции над ними Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок
Геометрическая и арифметическая прогрессии. Повторительно-обобщающий урок Частное степеней
Частное степеней Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс Неопределенный интеграл
Неопределенный интеграл Лекция+1+-+Предел+числовой+последовательности
Лекция+1+-+Предел+числовой+последовательности Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности
Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности Працюй творчо, відповідай швидко, точно і правильно
Працюй творчо, відповідай швидко, точно і правильно Описанная окружность треугольника
Описанная окружность треугольника Геометрическое путешествие. Дни математики в начальной школе (10.01.2019-31.01.2019) ГБОУ Школа № 170 им. А.П. Чехова
Геометрическое путешествие. Дни математики в начальной школе (10.01.2019-31.01.2019) ГБОУ Школа № 170 им. А.П. Чехова Введение в геометрию. Городской математический кружок. 6-7 классы
Введение в геометрию. Городской математический кружок. 6-7 классы Презентация
Презентация Таблица умножения и деления на 3
Таблица умножения и деления на 3 Характеристическое свойство арифметической прогрессии
Характеристическое свойство арифметической прогрессии Решение задач
Решение задач Найди лишний пример
Найди лишний пример Свойства ранга матрицы
Свойства ранга матрицы Типовые законы распределения непрерывных случайных величин. Лекция №8_
Типовые законы распределения непрерывных случайных величин. Лекция №8_ Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Вписанная окружность
Вписанная окружность Квадратный корень
Квадратный корень Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные