Повторение. треугольник (1)

Определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике

Теоремы синусов и косинусов

Формулы для вычисления площади треугольника

ТРЕУГОЛЬНИКИ
ЗАДАЧИ

№1

№2

№3

№4
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

№5
В треугольнике АВС АС=ВС. Внешний угол при вершине В равен 122∘. Найдите угол С. Ответ дайте в градусах.

№6
В треугольнике АВС АС=ВС=4 , угол С равен 30. Найдите высоту АН.

№7

№8
Острые углы прямоугольного треугольника равны 85° и 5°. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

№9
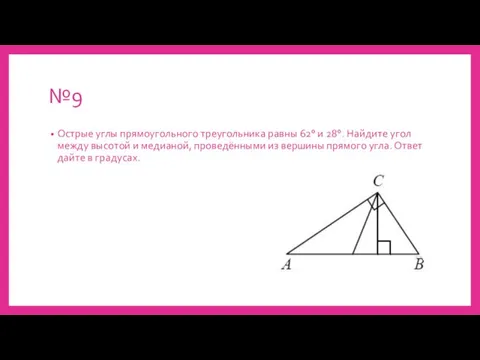
Острые углы прямоугольного треугольника равны 62° и 28°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

№10
В треугольнике ABC угол AСB равен 90°, cos A = 0,8, AC = 4. Отрезок CH ― высота треугольника ABC. Найдите длину отрезка AH.

№11

№12
Катеты прямоугольного треугольника равны 6 и 8. Найдите наибольшую среднюю линию треугольника.

№13

№14
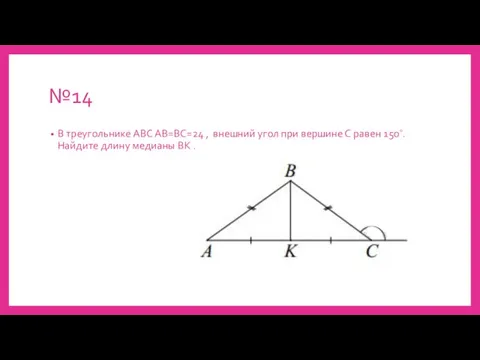
В треугольнике АВС АВ=ВС=24 , внешний угол при вершине С равен 150∘. Найдите длину медианы ВК .

№15

№16

№17
В равнобедренном треугольнике ABC с основанием AB угол В равен 27°. Найдите угол между стороной АС и высотой АН этого треугольника.

№18
В треугольнике ABC проведена биссектриса AL, угол ALC равен 140°, угол ABC равен 123°. Найдите угол ACB. Ответ дайте в градусах.

№19

№20

№21
В равнобедренном треугольнике ABC с основанием AB угол С равен 48°. Найдите угол между стороной AB и высотой АН этого треугольника.

№22
В треугольнике ABC известно на сторонах АВ и ВС отмечены точки М и К соответственно так, что ВМ : АВ = 1 : 2, а ВК : ВС = 4 : 5. Во сколько раз площадь треугольника ABC больше площади треугольника MBK?

№23
На стороне ВС прямоугольника АВСD, у которого АВ=12, АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.

№24
В равнобедренном треугольнике ABC боковые стороны AB = BC = 5, медиана BM = 4. Найдите cos∠BAC.