содержала 2n (n целое число = 0… ) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
2. Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
3. Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
4. Область должна быть как можно больше, а кол-во областей как можно меньше;
5. Области могут пересекаться;
6. Возможно несколько вариантов накрытия.
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности, составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
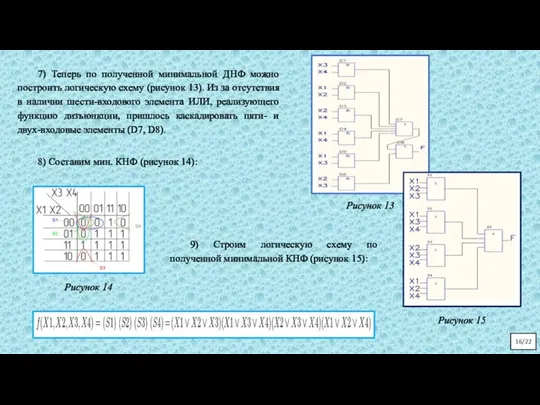
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки, которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
/22


















 Распределительный закон
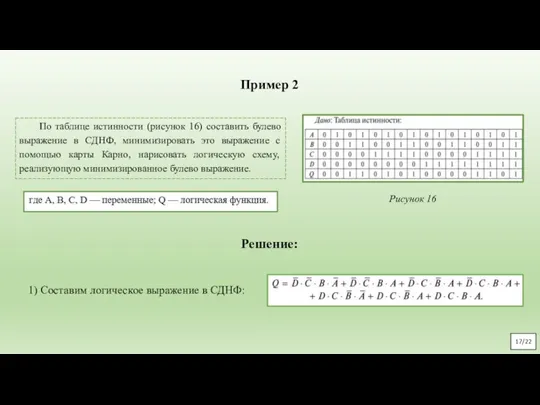
Распределительный закон Задания подготовительного этапа по программе Рудницкой В.Н Начальная школа XXI века
Задания подготовительного этапа по программе Рудницкой В.Н Начальная школа XXI века Применение теоремы Пифагора
Применение теоремы Пифагора Виды треугольников
Виды треугольников Нахождение площади и периметра прямоугольника. Применение формул на практике
Нахождение площади и периметра прямоугольника. Применение формул на практике Путешествие по математическому морю (2)
Путешествие по математическому морю (2) Уравнение плоской гармонической волны
Уравнение плоской гармонической волны Геометрические фигуры
Геометрические фигуры Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ
Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ  Решение иррациональных уравнений
Решение иррациональных уравнений История числа Пи
История числа Пи Презентация на тему Многогранники
Презентация на тему Многогранники  Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Методичні основи вивчення часу і одиниць його вимірювання
Методичні основи вивчення часу і одиниць його вимірювання Коэффициент. Упрощение выражений
Коэффициент. Упрощение выражений Презентация на тему Интегральное исчисление
Презентация на тему Интегральное исчисление  Звёздный час в математике
Звёздный час в математике Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13
Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13 Построение узла
Построение узла Отношения. Функции
Отношения. Функции Метрология. Погрешность измерений
Метрология. Погрешность измерений Задачи математической карусели. 4 класс
Задачи математической карусели. 4 класс Множество значений тригонометрических функций
Множество значений тригонометрических функций Решение задач с параметрами
Решение задач с параметрами Тождественные преобразования рациональных выражений
Тождественные преобразования рациональных выражений Число или цифра
Число или цифра Рівняння
Рівняння Сечения куба,призмы и пирамиды
Сечения куба,призмы и пирамиды