Содержание
- 2. Стереометрия – это геометрия в пространстве. Нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы
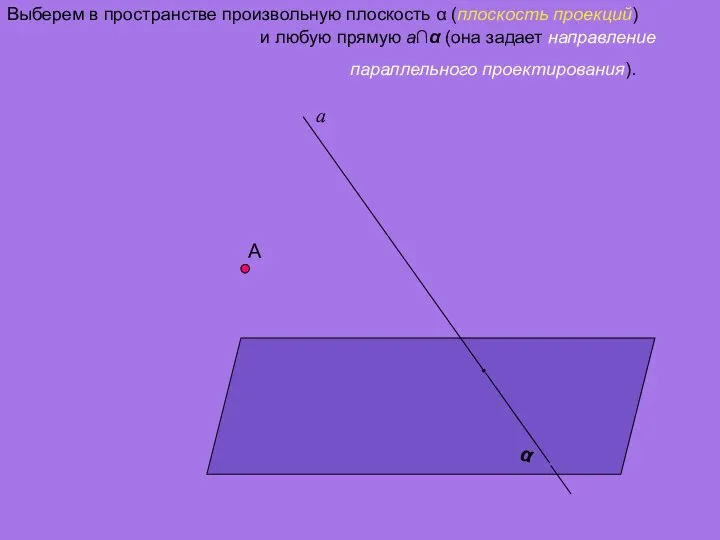
- 3. А Выберем в пространстве произвольную плоскость α (плоскость проекций) α и любую прямую a∩α (она задает
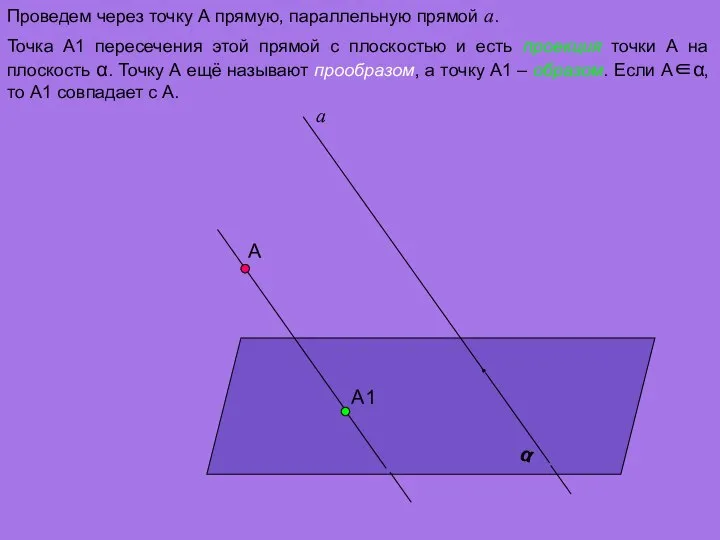
- 4. А α а Проведем через точку А прямую, параллельную прямой а. А1 Точка А1 пересечения этой
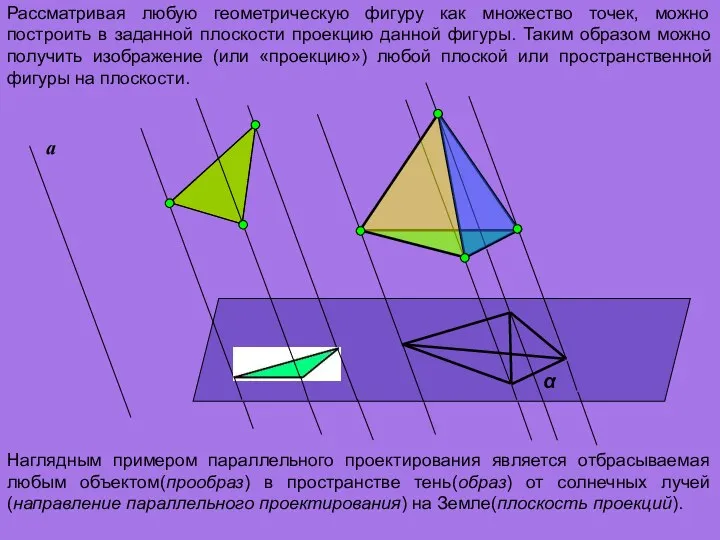
- 5. Рассматривая любую геометрическую фигуру как множество точек, можно построить в заданной плоскости проекцию данной фигуры. Таким
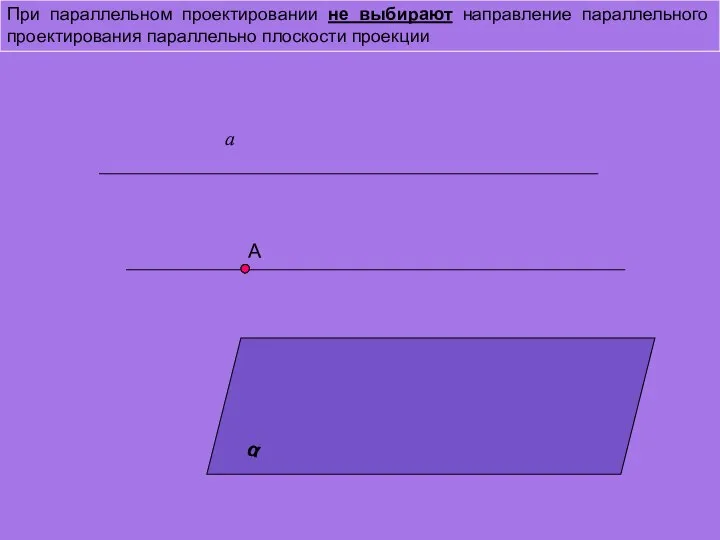
- 6. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции А а α
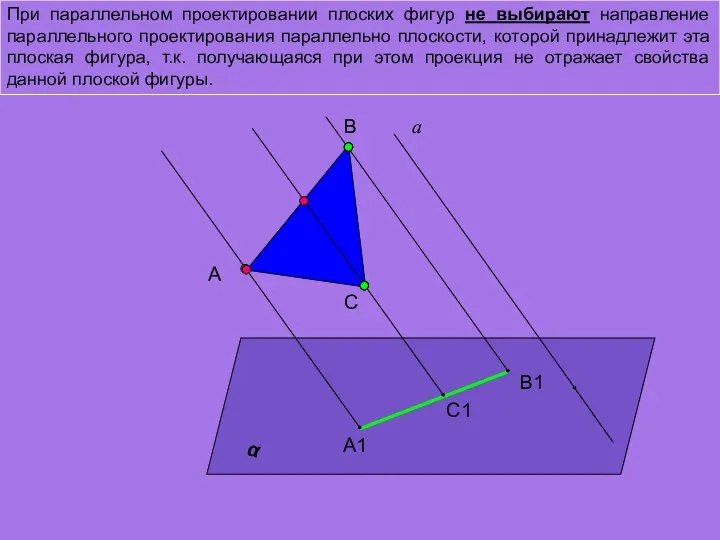
- 7. При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская
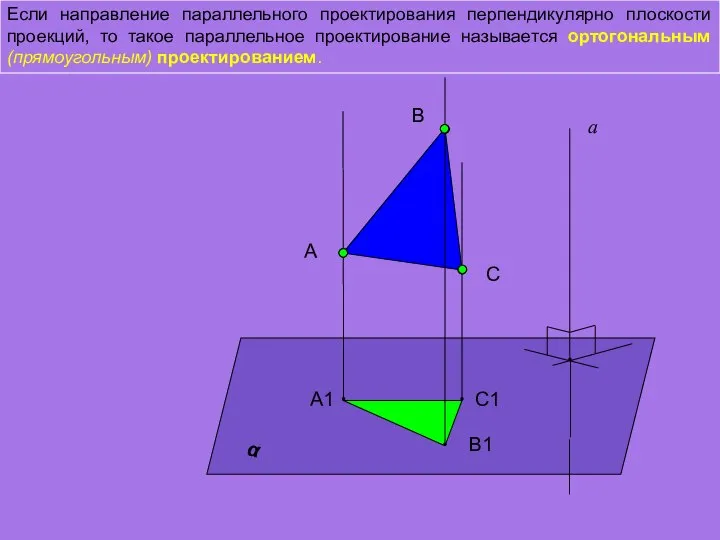
- 8. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным(прямоугольным) проектированием. А а
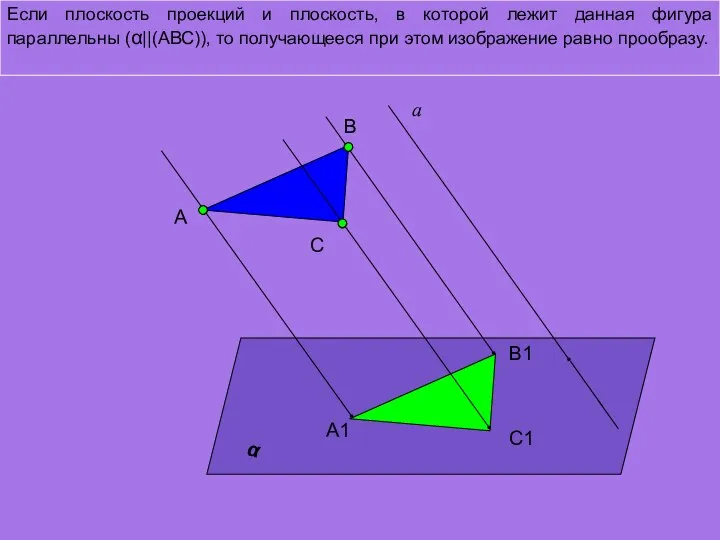
- 9. Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны (α||(АВС)), то получающееся при этом
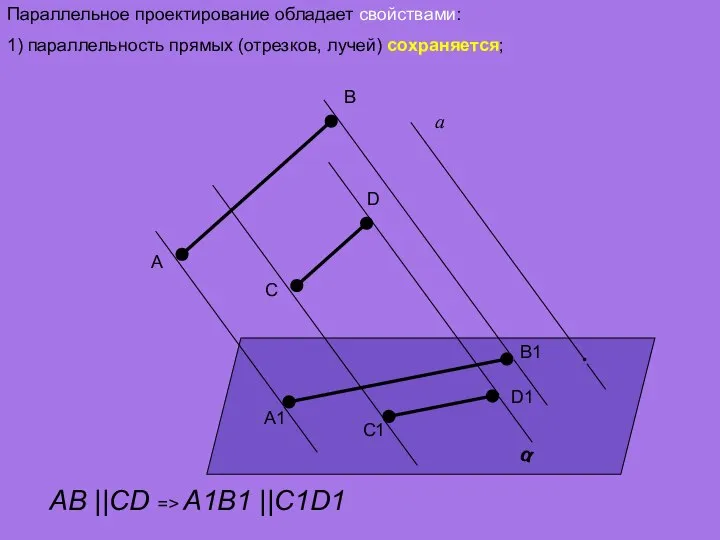
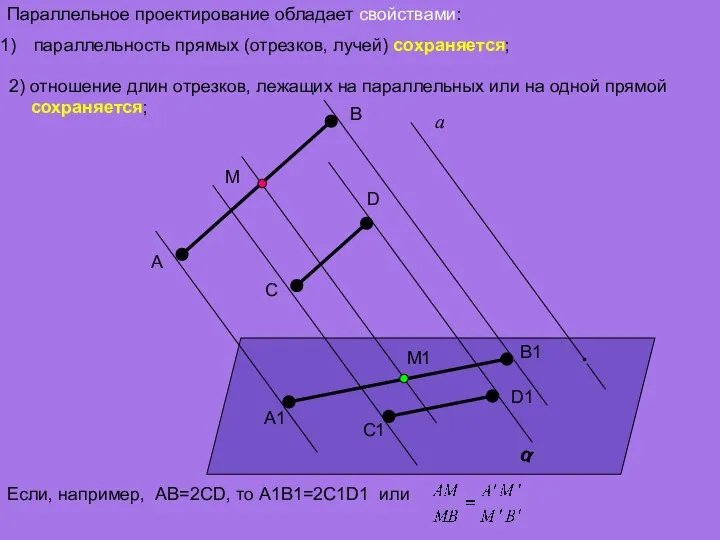
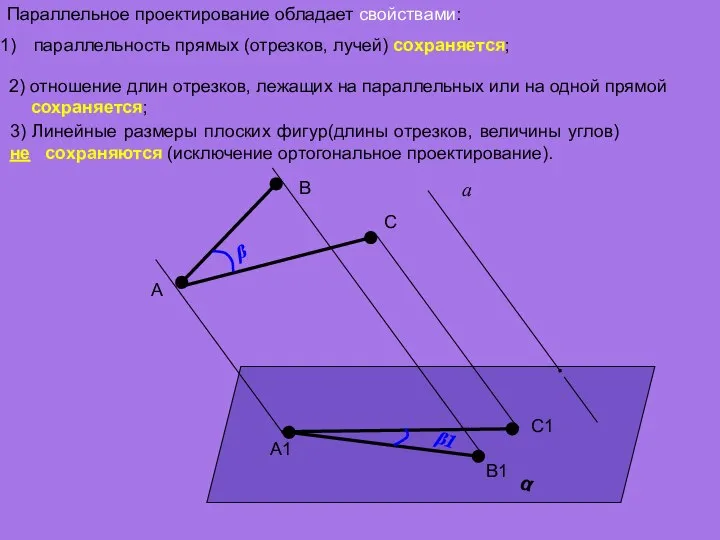
- 10. Параллельное проектирование обладает свойствами: 1) параллельность прямых (отрезков, лучей) сохраняется; α а A D C B
- 11. 2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется; Параллельное проектирование обладает свойствами:
- 12. Параллельное проектирование обладает свойствами: параллельность прямых (отрезков, лучей) сохраняется; α а A B A1 B1 3)
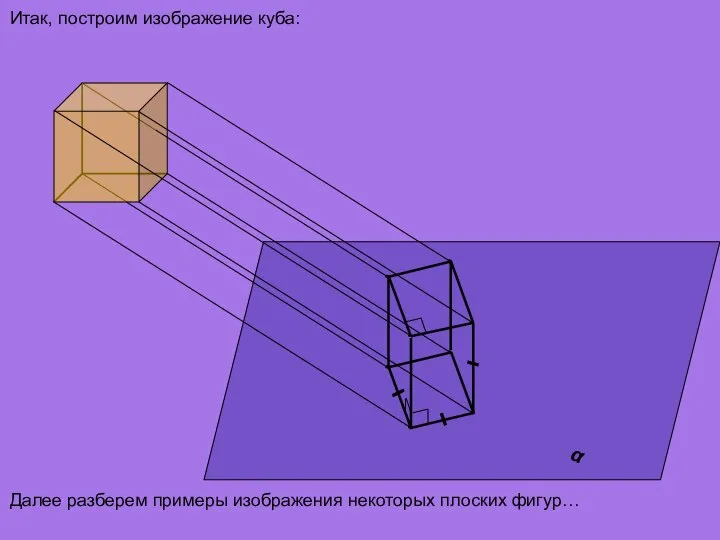
- 13. α Итак, построим изображение куба: Далее разберем примеры изображения некоторых плоских фигур…
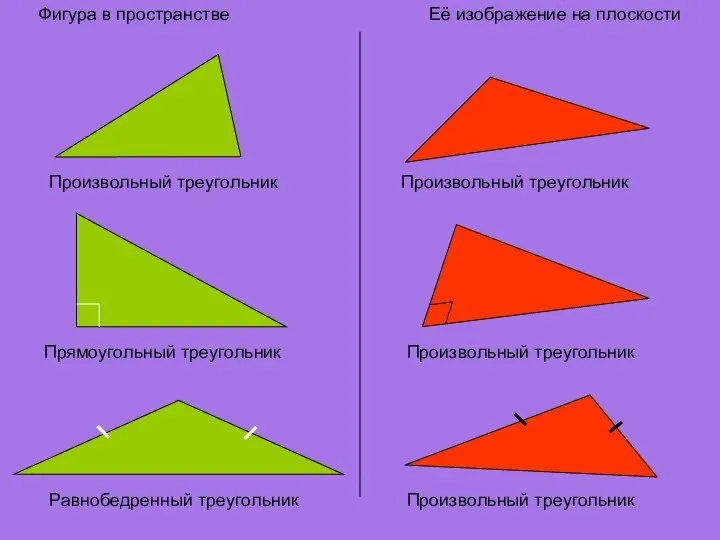
- 14. Фигура в пространстве Её изображение на плоскости Произвольный треугольник Произвольный треугольник Прямоугольный треугольник Произвольный треугольник Равнобедренный
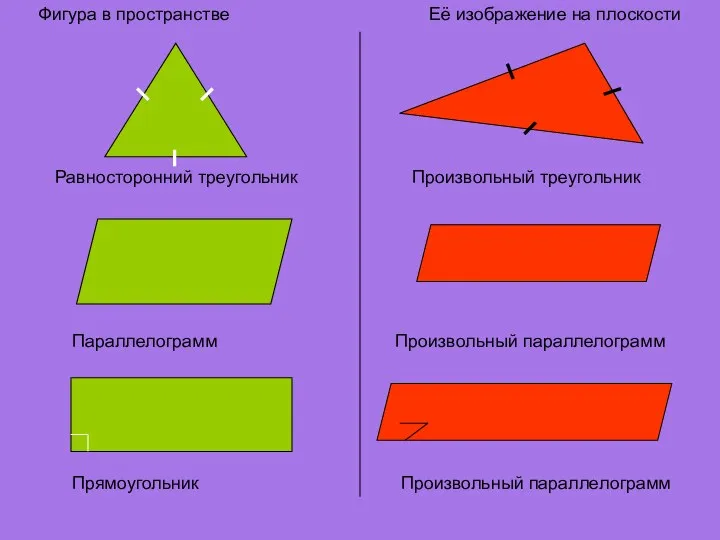
- 15. Фигура в пространстве Её изображение на плоскости Равносторонний треугольник Произвольный треугольник Параллелограмм Произвольный параллелограмм Прямоугольник Произвольный
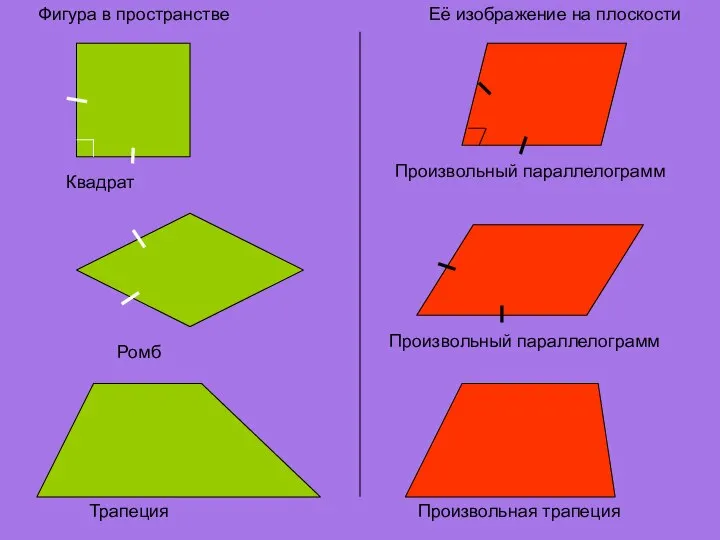
- 16. Фигура в пространстве Её изображение на плоскости Квадрат Произвольный параллелограмм Трапеция Произвольная трапеция Произвольный параллелограмм Ромб
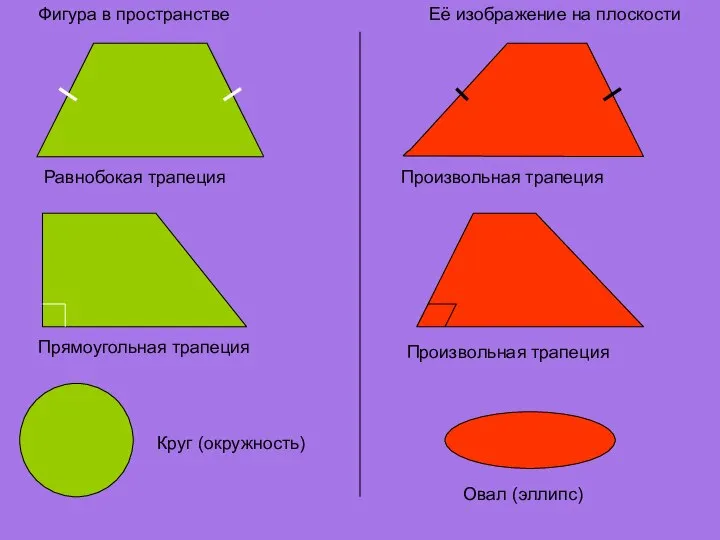
- 17. Фигура в пространстве Её изображение на плоскости Равнобокая трапеция Произвольная трапеция Прямоугольная трапеция Произвольная трапеция Круг
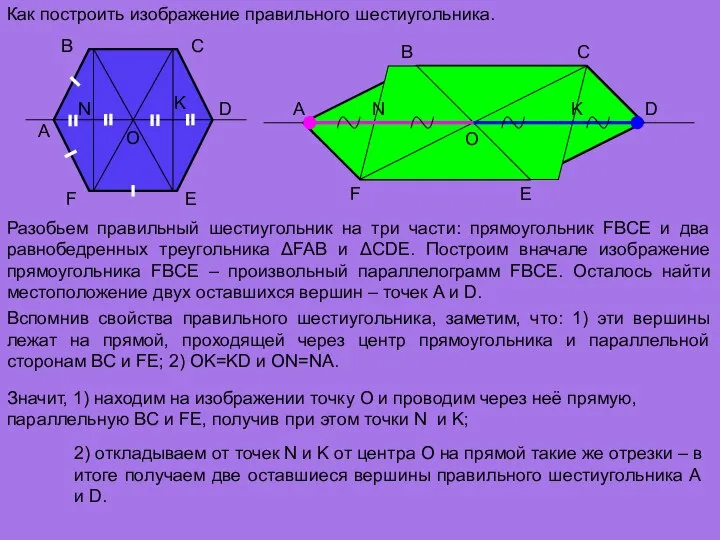
- 18. A B C D E F O Как построить изображение правильного шестиугольника. F A B C
- 20. Скачать презентацию

 Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Презентация на тему Составление и решение задач разного типа различными способами
Презентация на тему Составление и решение задач разного типа различными способами  Параллельные прямые. Тест
Параллельные прямые. Тест Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Основы тригонометрии
Основы тригонометрии Презентация на тему Простейшая геометрия
Презентация на тему Простейшая геометрия  Затухающий гармонический осциллятор. Лекция 3
Затухающий гармонический осциллятор. Лекция 3 Логика высказываний и булевы алгебры (Boolean Algebra and Logic)
Логика высказываний и булевы алгебры (Boolean Algebra and Logic) Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат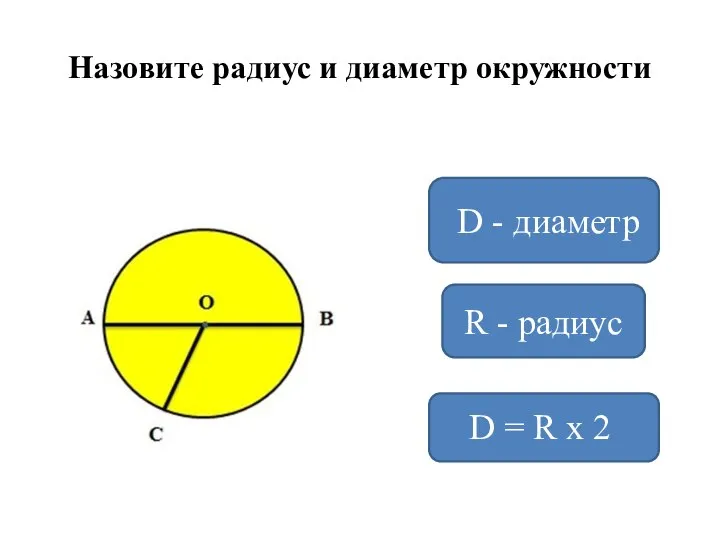 Радиус и диаметр окружности
Радиус и диаметр окружности Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Координаты и векторы
Координаты и векторы Вероятность и статистика
Вероятность и статистика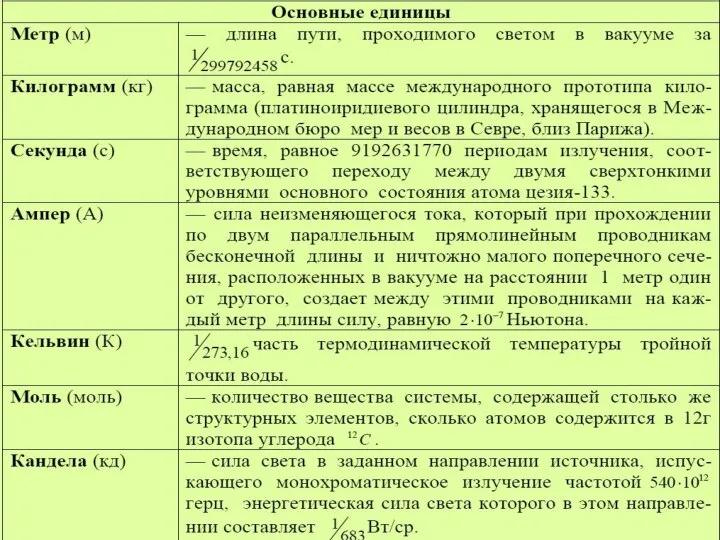 Основные единиціы
Основные единиціы Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы
Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация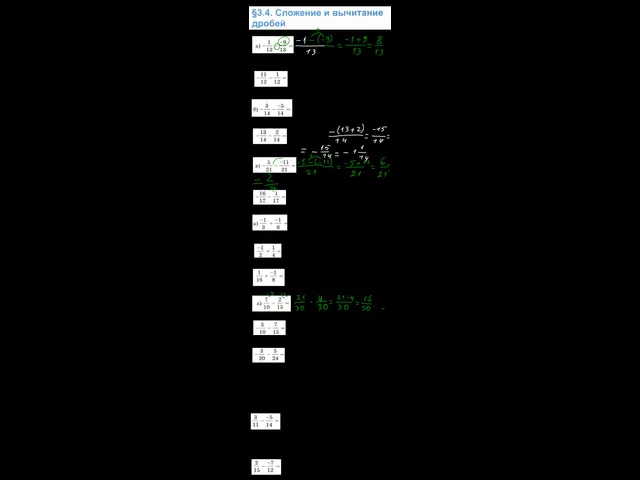 Сложение и вычитание рациональных чисел
Сложение и вычитание рациональных чисел Уравнение средней
Уравнение средней Надежность технических систем
Надежность технических систем Квадратные уравнения
Квадратные уравнения Число. Натуральный ряд. Абсолютная шкала измерений
Число. Натуральный ряд. Абсолютная шкала измерений Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования Умножение дробей на натуральное число
Умножение дробей на натуральное число Формулы дифференцирования
Формулы дифференцирования Длина окружности
Длина окружности Многозначные числа. Тест
Многозначные числа. Тест