Правильные многогранники

Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
Многогранник называется правильным, если:
1.он выпуклый;
2.все его грани являются равными правильными многоугольниками;
3.в каждой его вершине сходится одинаковое число рёбер.

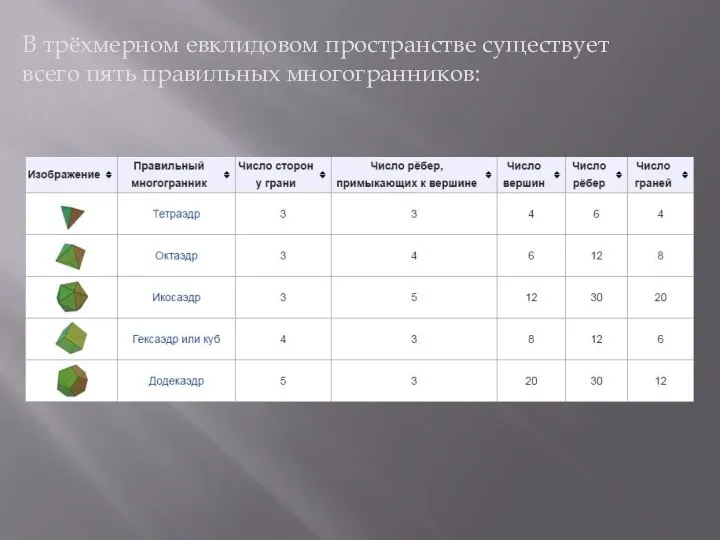
В трёхмерном евклидовом пространстве существует всего пять правильных многогранников:

Правильный тетраэдр
Составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно сумма плоских углов при каждой вершине равна 180°.
Подобное строение имеют молекулы метана, кристаллы белого фосфора и фосфорноватистая кислота. Решетка алмаза так же по строению напоминает тетраэдр.

Правильный октаэдр
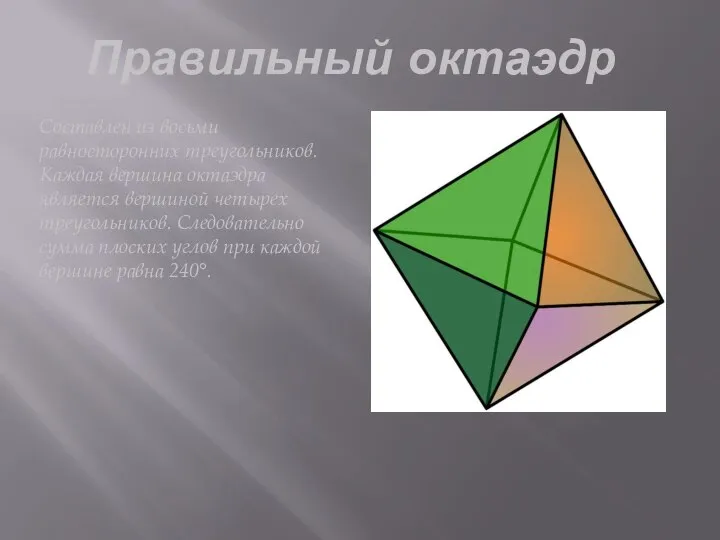
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно сумма плоских углов при каждой вершине равна 240°.

Правильный икосаэдр
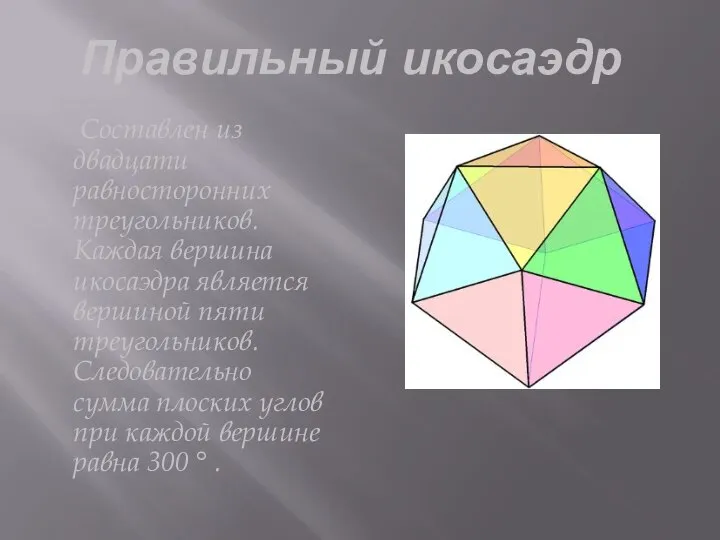
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно сумма плоских углов при каждой вершине равна 300 ° .

Куб
Составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 °.

Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.