Содержание
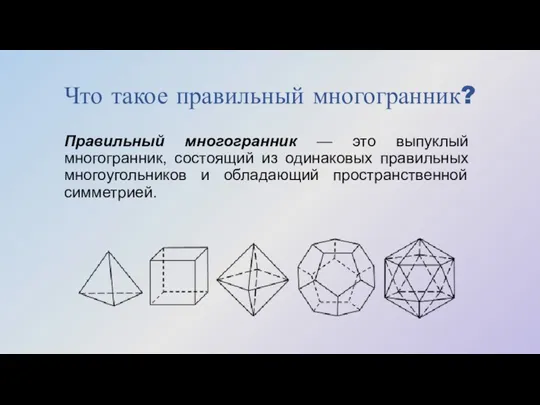
- 2. Что такое правильный многогранник? Правильный многогранник — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и
- 3. История Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах,
- 4. История В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох)
- 5. История Многие утверждают, что Пифагору были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра
- 6. История Правильные многогранники характерны для философии Платона, в честь которого и получили название «Платоновы тела». Платон
- 7. Платон Платон — афинский философ классического периода Древней Греции, основатель платонической школы мысли и Академии, первого
- 8. Количество правильных многогранников Существует не более пяти различных видов правильных многогранников. Доказательство: Из определения правильного многогранника
- 9. Теорема Эйлера Пусть В – число вершин выпуклого многогранника, Р – число его ребер и Г
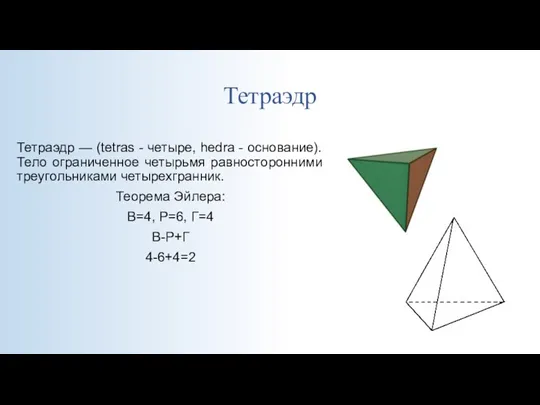
- 10. Тетраэдр Тетраэдр — (tetras - четыре, hedra - основание). Тело ограниченное четырьмя равносторонними треугольниками четырехгранник. Теорема
- 11. Гексаэдр Гексаэдр – (hex - шесть, hedra - основание). Куб, тело ограниченное шестью квадратами. Теорема Эйлера:
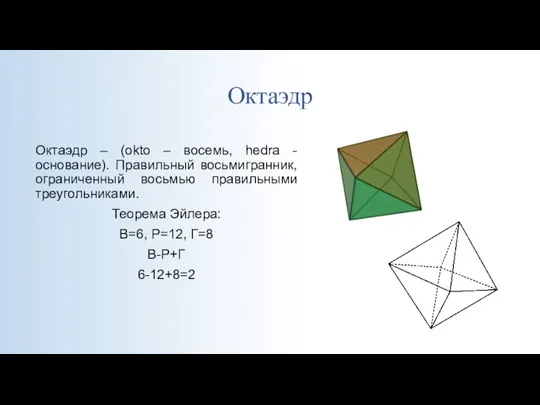
- 12. Октаэдр Октаэдр – (okto – восемь, hedra - основание). Правильный восьмигранник, ограниченный восьмью правильными треугольниками. Теорема
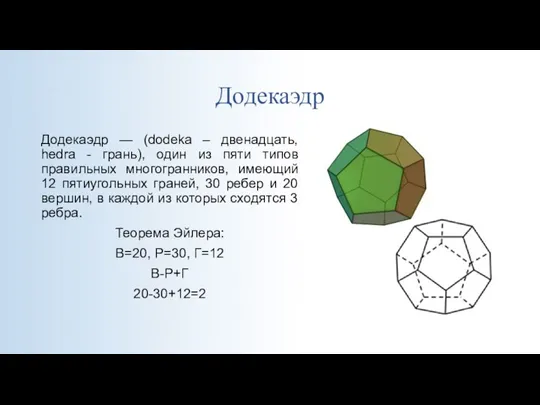
- 13. Додекаэдр Додекаэдр — (dodeka – двенадцать, hedra - грань), один из пяти типов правильных многогранников, имеющий
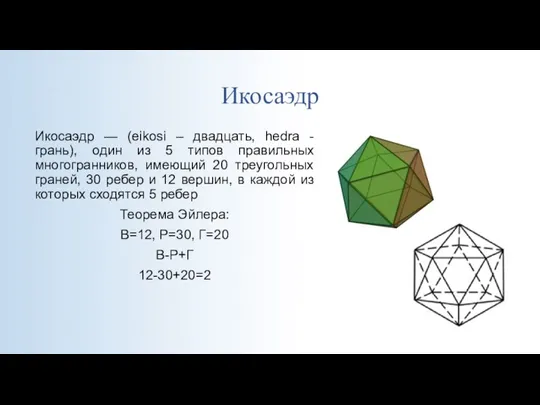
- 14. Икосаэдр Икосаэдр — (eikosi – двадцать, hedra - грань), один из 5 типов правильных многогранников, имеющий
- 16. Скачать презентацию








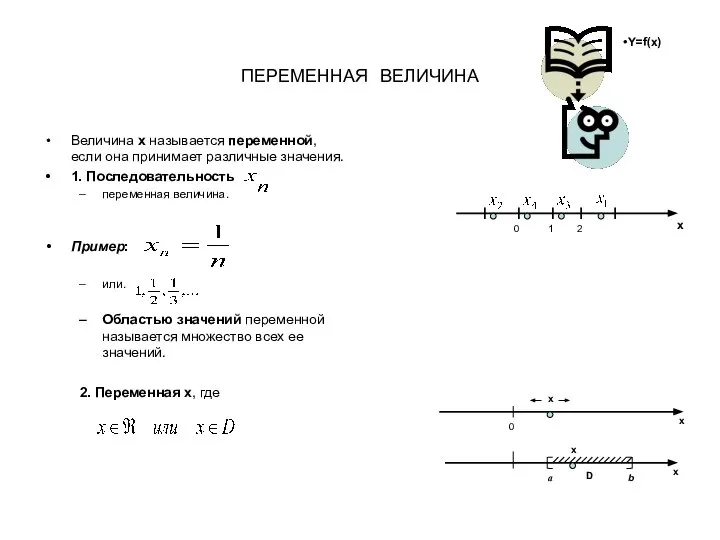 Переменная величина
Переменная величина Квадратный корень
Квадратный корень Соответствия величин вычисления. 11 класс, 9 задание
Соответствия величин вычисления. 11 класс, 9 задание Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2
Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2 Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс)  Л 5 Функция одной переменной
Л 5 Функция одной переменной Понятие ”тетраэдр”
Понятие ”тетраэдр” Графы и их применение при решении задач
Графы и их применение при решении задач Аксиомы стереометрии
Аксиомы стереометрии Теория графов. Основные понятия
Теория графов. Основные понятия Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Линейные неравенства с параметром
Линейные неравенства с параметром Решение задач
Решение задач Визуализация операций над эллиптическими кривыми
Визуализация операций над эллиптическими кривыми Область определения функции
Область определения функции Свойства алгоритма
Свойства алгоритма Движение по окружности
Движение по окружности Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Типы задач на проценты
Типы задач на проценты Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Измеряй и сравнивай
Измеряй и сравнивай Тела вращения. Открытый урок
Тела вращения. Открытый урок Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника 3.3. Понятие функции
3.3. Понятие функции Как помочь ребенку понять математику. Вебинар 2
Как помочь ребенку понять математику. Вебинар 2 Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных
Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных Theorem of rational root with integral coefficients
Theorem of rational root with integral coefficients