Содержание
- 2. История возникновения пределов Интуитивно понятие о предельном переходе при вычислении площадей и объемов различных геометрических тел
- 3. История возникновения пределов Дальнейшее свое применение теория пределов получила при создании дифференциального и интегрального исчислений в
- 4. История возникновения пределов Впервые определение понятия предела было введено в работе английского математика Джона Валлиса (1616-1703)
- 5. История возникновения пределов В 19 веке в работах великого французского математика и механика Огюстена Луи Коши
- 6. История возникновения пределов Дальнейшим развитием этой теории занимались немецкий математик Карл Теодор Вильгельм Вейерштрасс (1815-1897) и
- 7. Предел функции на бесконечности. Бесконечность — используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в
- 8. Окрестность точки
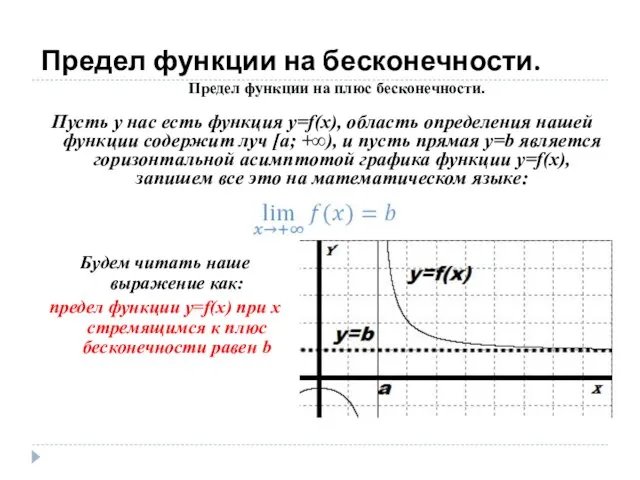
- 9. Предел функции на бесконечности. Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч
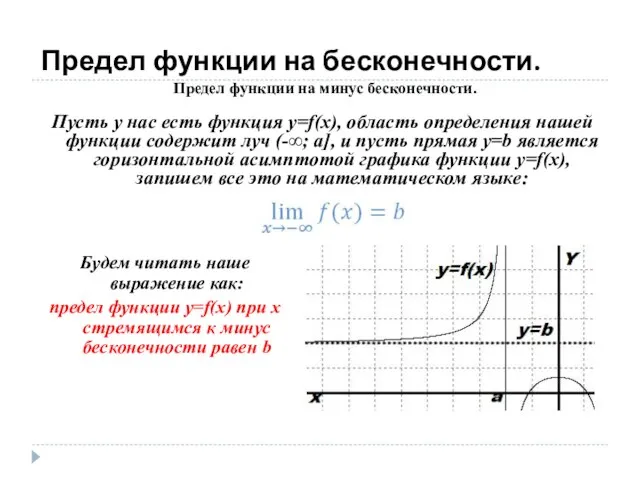
- 10. Предел функции на бесконечности. Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч
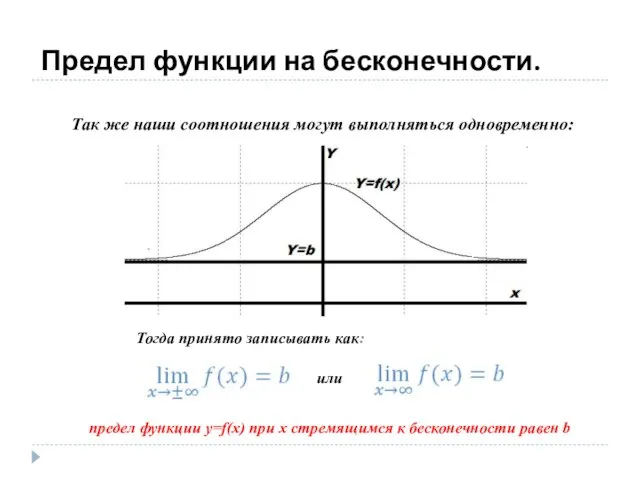
- 11. Предел функции на бесконечности. Так же наши соотношения могут выполняться одновременно: Тогда принято записывать как: или
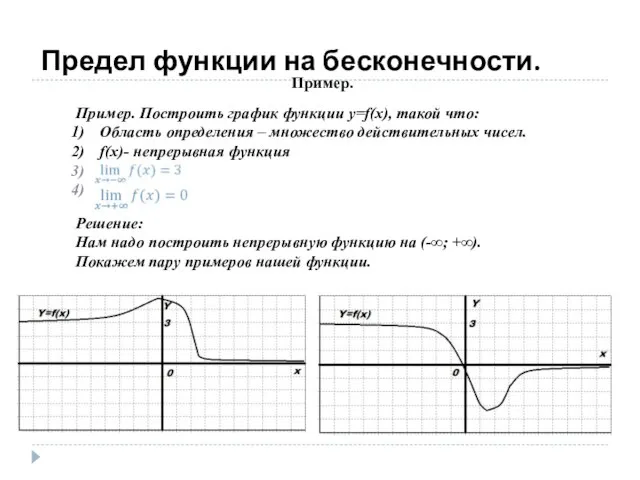
- 12. Предел функции на бесконечности. Пример. Пример. Построить график функции y=f(x), такой что: Область определения – множество
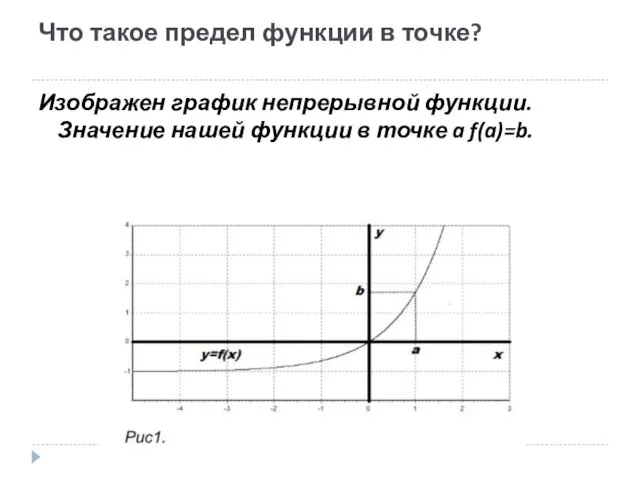
- 13. Что такое предел функции в точке? Изображен график непрерывной функции. Значение нашей функции в точке a
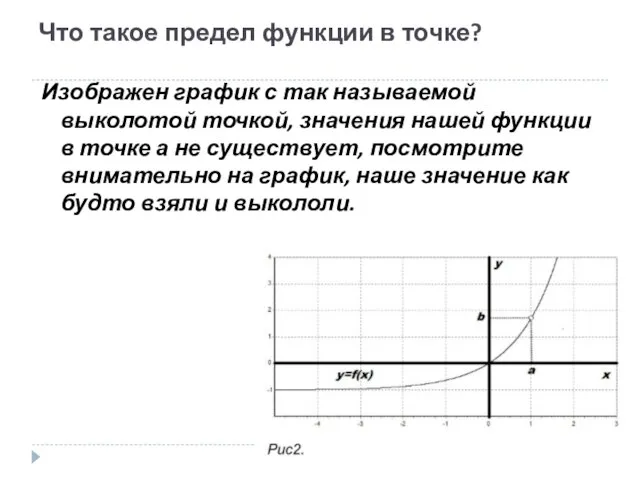
- 14. Что такое предел функции в точке? Изображен график с так называемой выколотой точкой, значения нашей функции
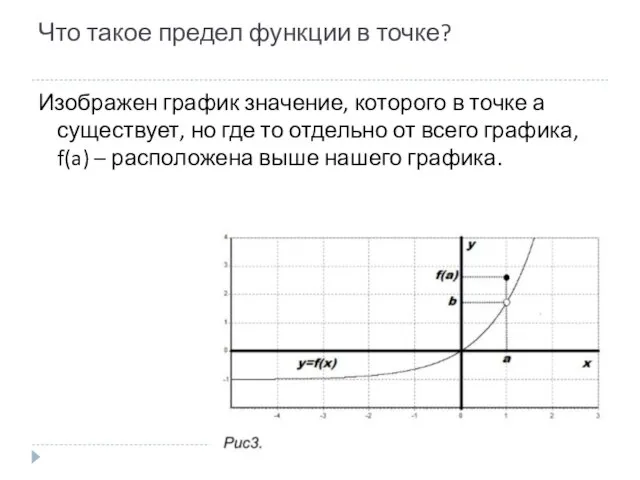
- 15. Что такое предел функции в точке? Изображен график значение, которого в точке а существует, но где
- 16. Что такое предел функции в точке? На наших рисунках изображены графики трех разных функций. Если мы
- 22. Предел функции на бесконечности. Для вычисления предела на бесконечности пользуются несколькими утверждениями: 1) Для любого натурально
- 23. Предел функции на бесконечности. Пример. Найти Решение. Разделим числитель и знаменатель дроби на x. Вспомним предел
- 24. Предел функции на бесконечности. Пример. Найти предел функции y=f(x), при x стремящимся к бесконечности. Решение. Разделим
- 25. Предел функции на бесконечности. Пример. Найти предел функции y=f(x), при x стремящимся к бесконечности. Решение. Разделим
- 26. Найти предел функции: Наша функция непрерывна в точке x=2, тогда воспользуемся определением непрерывности функции в точке,
- 27. Найти предел функции: Давайте посмотрим не обращается ли знаменатель нашей функции при x=π/2 в нуль: Знаменатель
- 28. Найти предел функции: Подставим x=2 в знаменатель нашей дроби, получили 0, но на ноль делить нельзя.
- 29. Найти предел функции: Подставим x=1 в знаменатель нашей дроби, получили 0, но на ноль делить нельзя.
- 31. Скачать презентацию


















 Построение прямоугольника от двух прямых углов. Прямоугольная коробка
Построение прямоугольника от двух прямых углов. Прямоугольная коробка Рейтинг-контроль
Рейтинг-контроль Презентация на тему Законы алгебры логики
Презентация на тему Законы алгебры логики  Прямоугольные треугольники
Прямоугольные треугольники Четырёхугольник
Четырёхугольник Пропорция
Пропорция Произведение дробей, обратных друг другу
Произведение дробей, обратных друг другу Область определения функции
Область определения функции Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Практическая работа
Практическая работа Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Предел последовательности. Практическая работа № 24
Предел последовательности. Практическая работа № 24 Брейн-ринг. Математика
Брейн-ринг. Математика Презентация на тему Технологии развивающего обучения в практике учителя математики
Презентация на тему Технологии развивающего обучения в практике учителя математики  Выделение в число общего количества единиц любого разряда
Выделение в число общего количества единиц любого разряда Тригонометрия. Восхождение на пик
Тригонометрия. Восхождение на пик Доли и дроби
Доли и дроби Методика изучения массы
Методика изучения массы Преобразование графиков функций. Математический диктант
Преобразование графиков функций. Математический диктант Виды треугольников. 3 класс
Виды треугольников. 3 класс Преобразование выражений с помощью формул сокращенного умножения
Преобразование выражений с помощью формул сокращенного умножения Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Элементы статистической обработки данных
Элементы статистической обработки данных Элементы комбинаторики АТ
Элементы комбинаторики АТ Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Презентация на тему Логарифмы
Презентация на тему Логарифмы  Операции над матрицами
Операции над матрицами