Содержание
- 2. Зачатки тригонометрических познаний зародились в древности
- 3. Николай КОПЕРНИК (1473 – 1543) Франсуа ВИЕТ (1540 - 1603) Евклид (ок. 325 – 265 до
- 4. Иоганн КЕПЛЕР (1571 – 1630) Исаак НЬЮТОН (1643 – 1727) Готфрид ЛЕЙБНИЦ (1646 – 1716) С
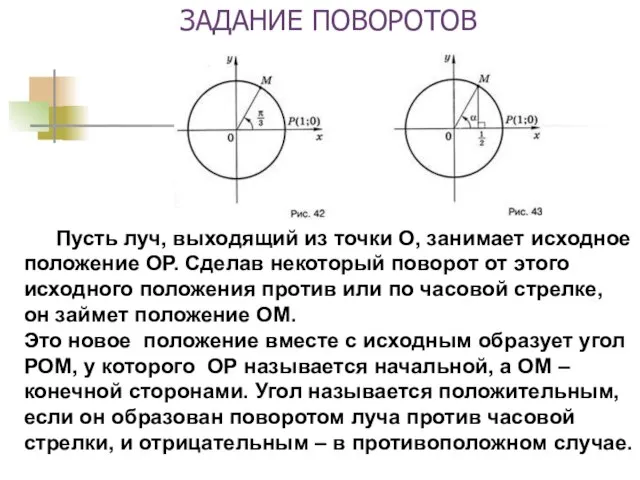
- 5. ЗАДАНИЕ ПОВОРОТОВ Пусть луч, выходящий из точки О, занимает исходное положение ОР. Сделав некоторый поворот от
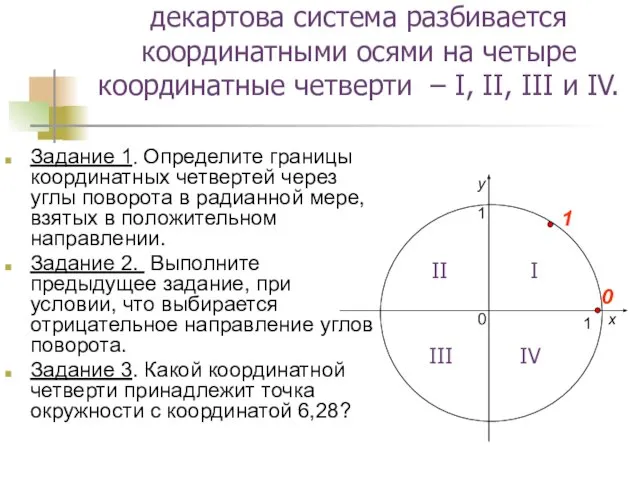
- 6. декартова система разбивается координатными осями на четыре координатные четверти – I, II, III и IV. Задание
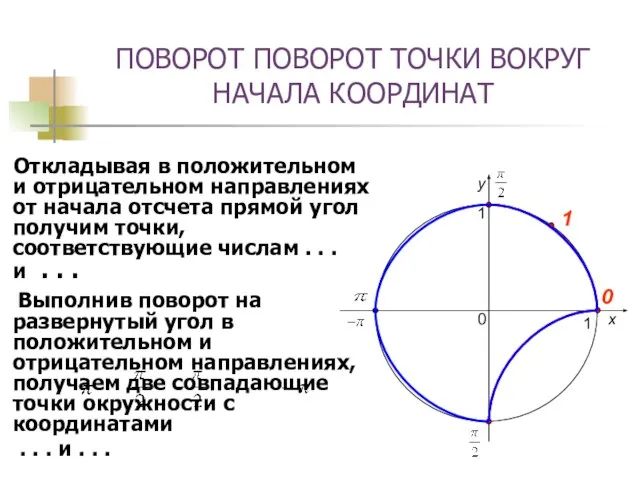
- 7. ПОВОРОТ ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Откладывая в положительном и отрицательном направлениях от начала отсчета прямой
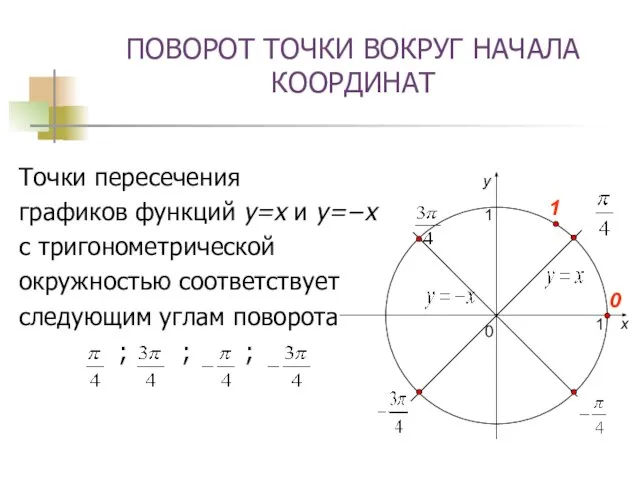
- 8. ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Точки пересечения графиков функций y=x и y=−x с тригонометрической окружностью соответствует
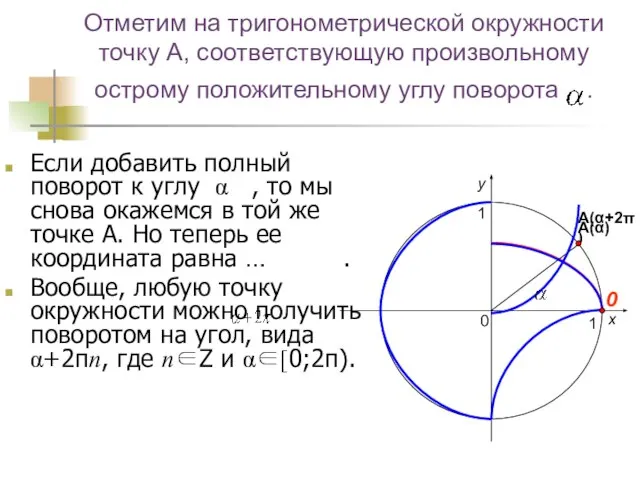
- 9. Отметим на тригонометрической окружности точку А, соответствующую произвольному острому положительному углу поворота . Если добавить полный
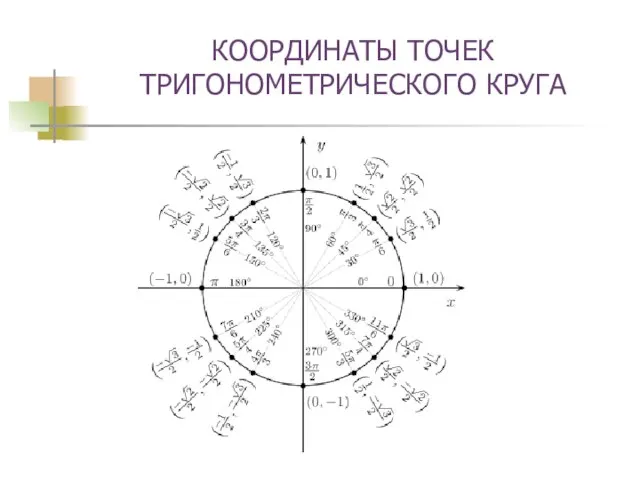
- 10. КООРДИНАТЫ ТОЧЕК ТРИГОНОМЕТРИЧЕСКОГО КРУГА
- 12. Скачать презентацию



 Проценты. Проценты в древности
Проценты. Проценты в древности Математические забавы
Математические забавы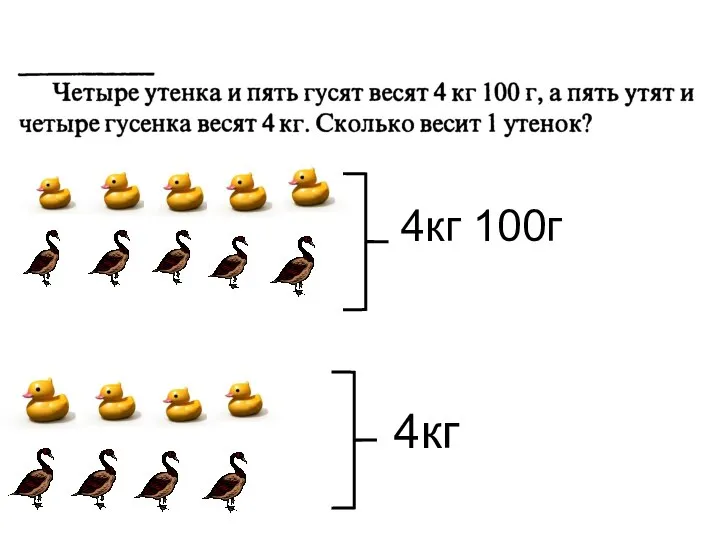 Уравнение. Задача на определение веса
Уравнение. Задача на определение веса Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни
Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни Свойства определенных интегралов
Свойства определенных интегралов Построение угла, равного данному
Построение угла, равного данному Задачи с кубиками
Задачи с кубиками Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)
Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3) Арифметические действия с десятичными дробями (организация проекта Комплектование сладкого подарка)
Арифметические действия с десятичными дробями (организация проекта Комплектование сладкого подарка) Решаем примеры
Решаем примеры Математическое описание случайных явлений
Математическое описание случайных явлений Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св
Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св Считалка для ворон Андрея Усачева. Традиционный показ по методике Домана
Считалка для ворон Андрея Усачева. Традиционный показ по методике Домана Леонардо да Винчи
Леонардо да Винчи Построение кривой времени t=f(s) методом инженера Лебедева
Построение кривой времени t=f(s) методом инженера Лебедева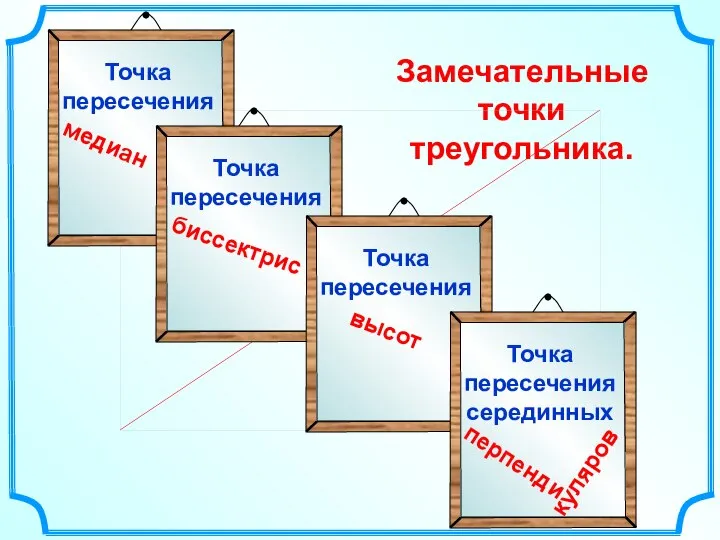 Замечательные точки треугольника
Замечательные точки треугольника 5 сказочных загадок по математике
5 сказочных загадок по математике Подготовка к контрольной работе
Подготовка к контрольной работе Случайные события. Вероятность случайного события
Случайные события. Вероятность случайного события Функция, ее график и свойства
Функция, ее график и свойства Элементы комбинаторики АТ
Элементы комбинаторики АТ Тест по теме: Объем наклонной призмы, пирамиды и конуса. Вариант 2
Тест по теме: Объем наклонной призмы, пирамиды и конуса. Вариант 2 Устно решай – свой край узнавай
Устно решай – свой край узнавай Площадь четырёхугольника
Площадь четырёхугольника Решение задач. Урок 22
Решение задач. Урок 22 Математика с котом Леопольдом
Математика с котом Леопольдом Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций