Слайд 2Взаимное расположение прямой и окружности
Прямая может не иметь с окружностью общих точек;
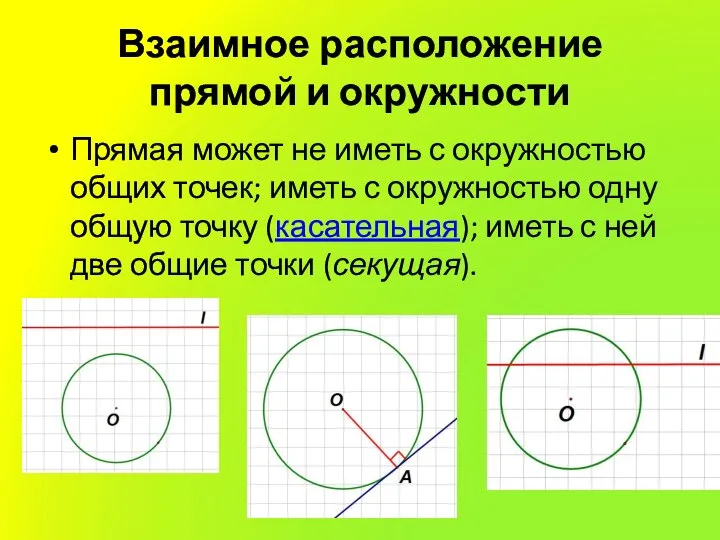
иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
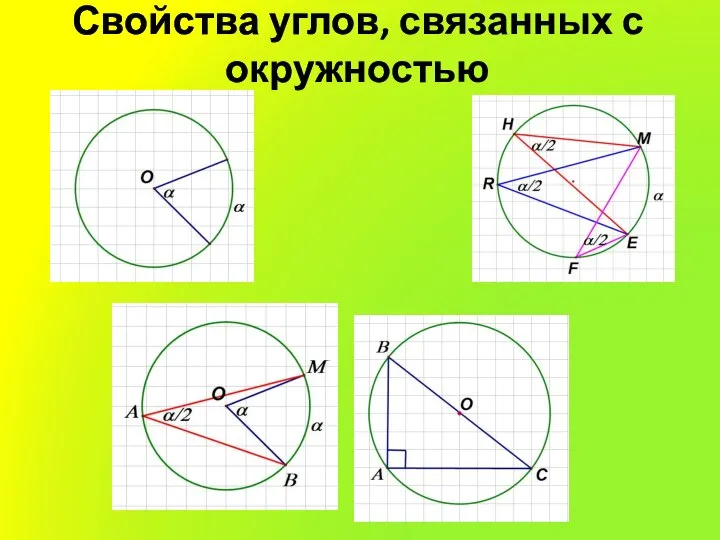
Слайд 3Свойства углов, связанных с окружностью
Слайд 4Угол между касательной и секущей, исходящих из одной точки
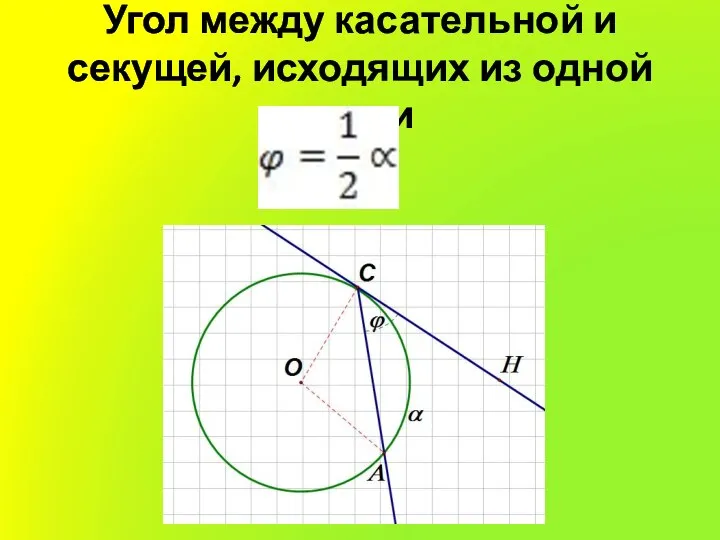
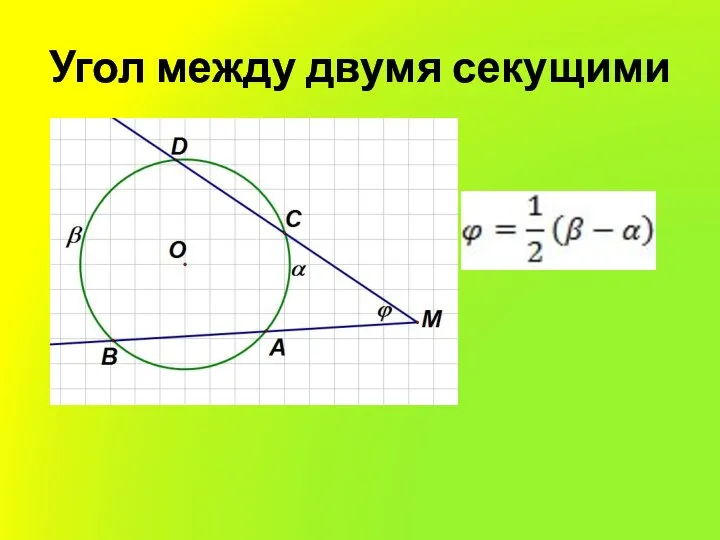
Слайд 6Угол между секущей и касательной
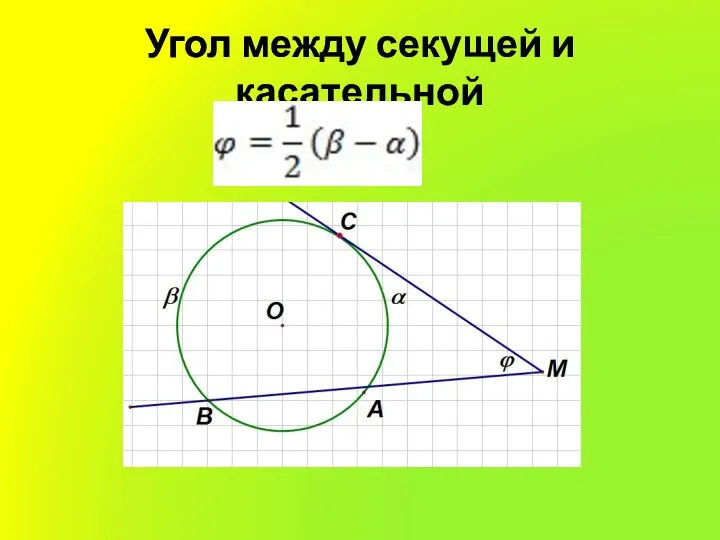
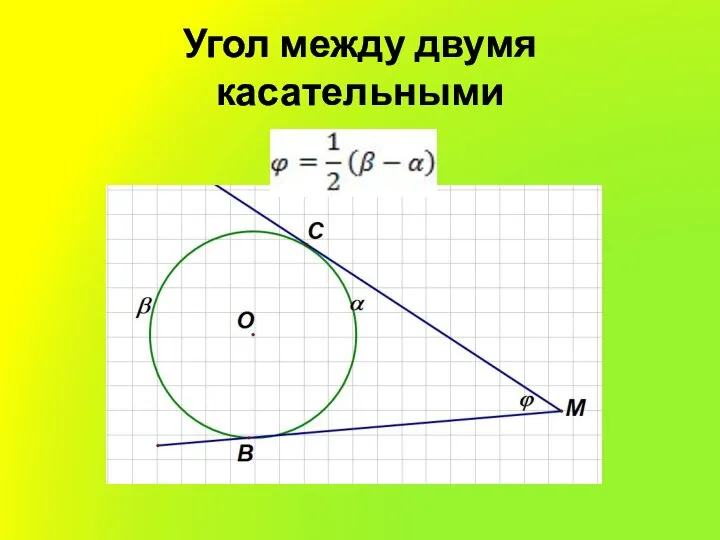
Слайд 7Угол между двумя касательными
Слайд 9Окружность. Свойства хорд, секущих, касательной.
Точка касания двух окружностей лежит на линии, соединяющей
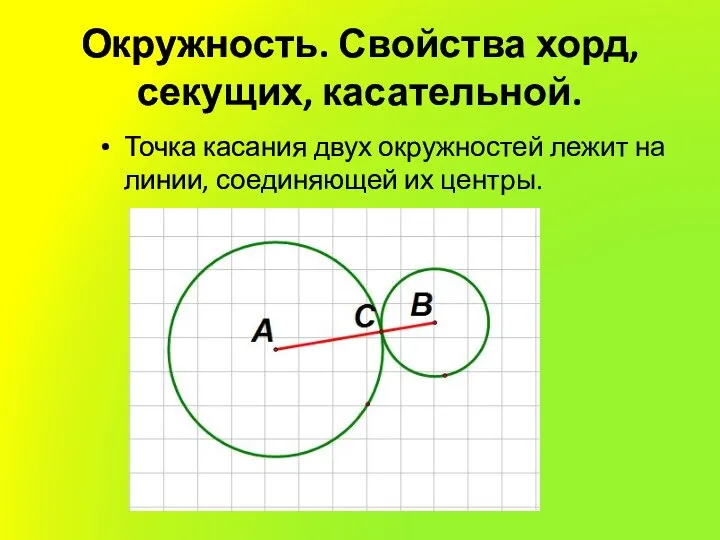
их центры.
Слайд 10
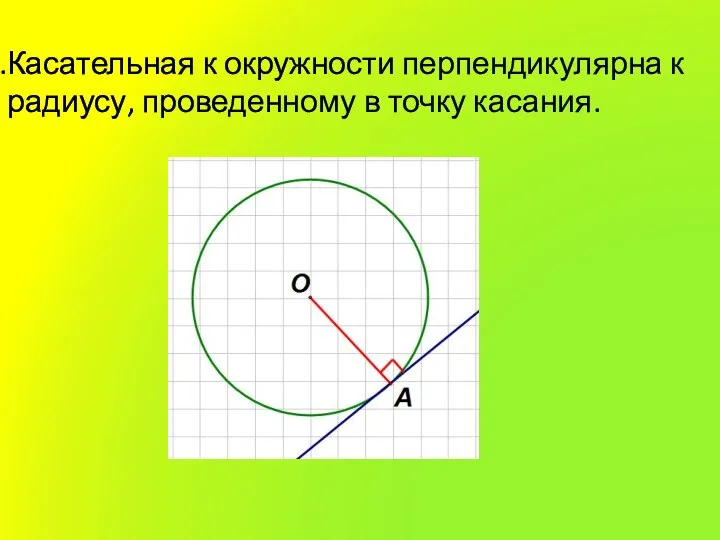
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Слайд 11Окружность. Свойства хорд, секущих, касательной.
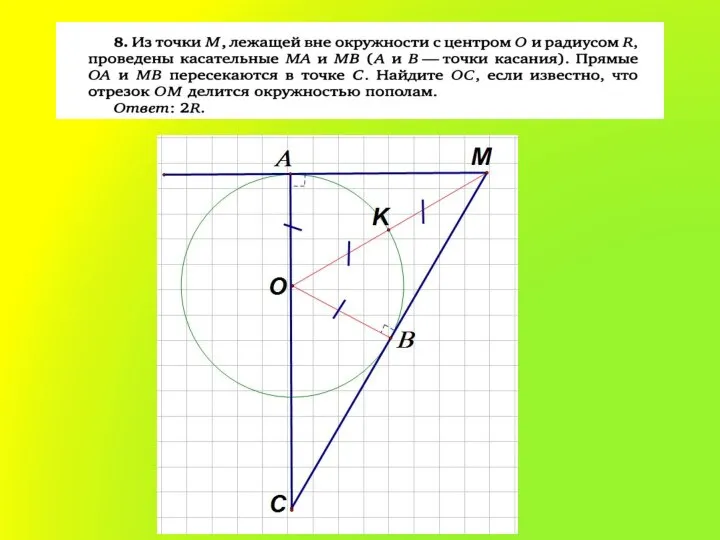
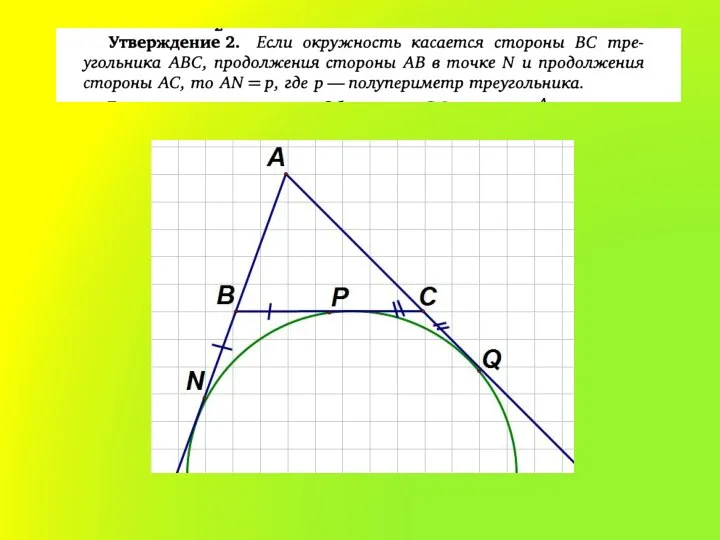
2. Отрезки касательных к окружности, проведенных из одной
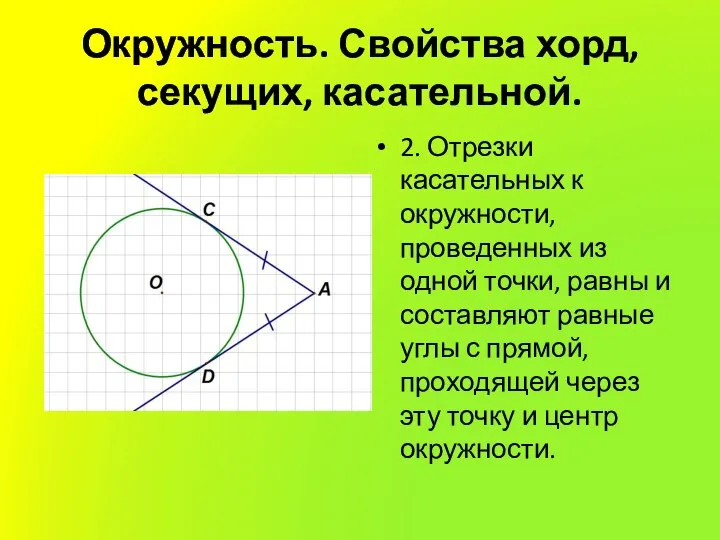
точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Слайд 12Окружность. Свойства хорд, секущих, касательной.
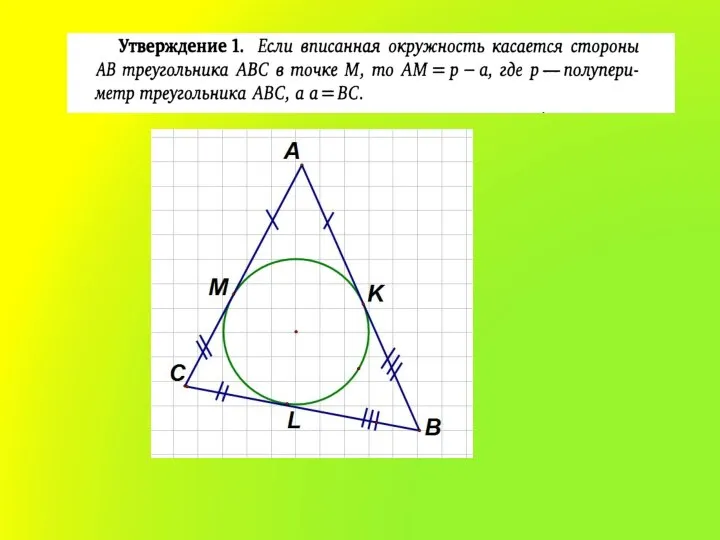
3. Диаметр (радиус), перпендикулярный к хорде, делит эту

хорду и обе стягиваемые ею дуги пополам.
Слайд 13Окружность. Свойства хорд, секущих, касательной.
4. Дуги, заключенные между параллельными хордами, равны.
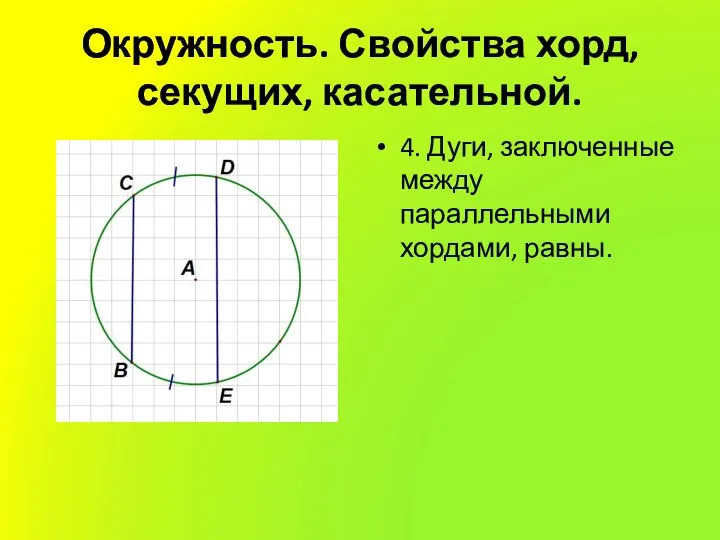
Слайд 14Окружность. Свойства хорд, секущих, касательной.
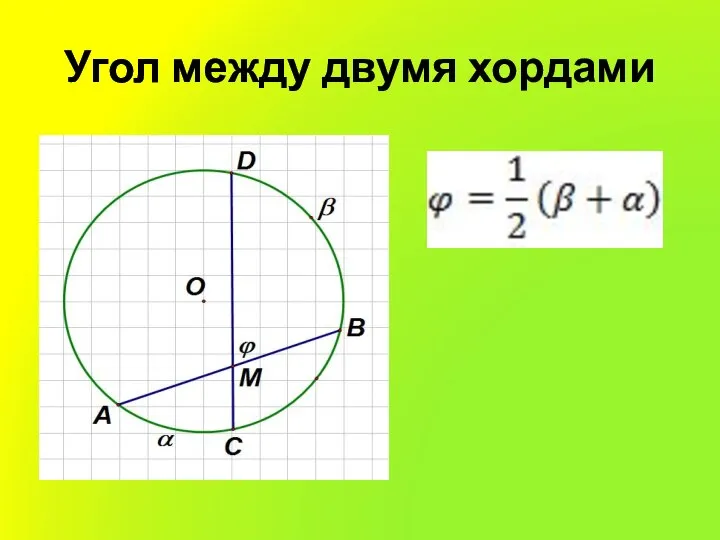
5. Если две хорды окружности, AB и CD пересекаются в точке M, то
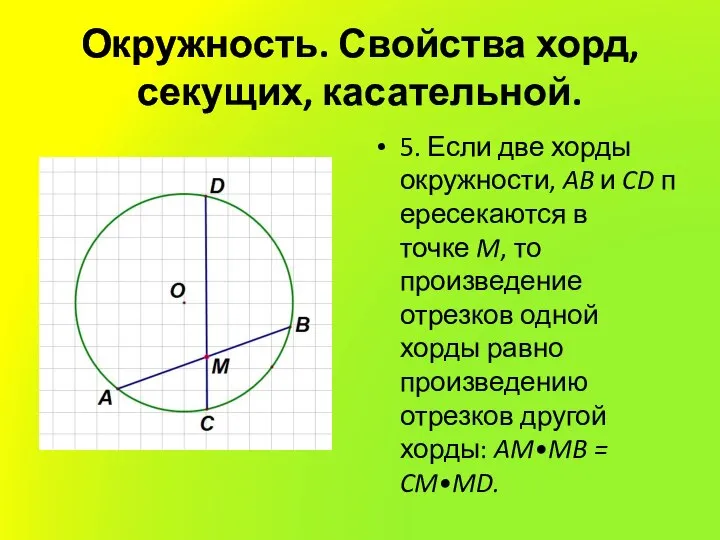
произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Слайд 15Теорема о касательной и секущей
6. Если из точки, лежащей вне окружности, проведены касательная и секущая,
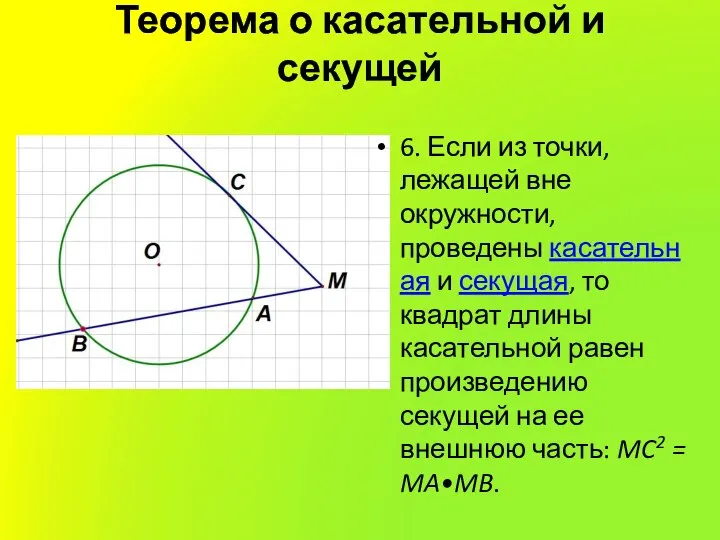
то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB.
Слайд 16Теорема о секущих
7. Если из точки, лежащей вне окружности, проведены две секущие, то
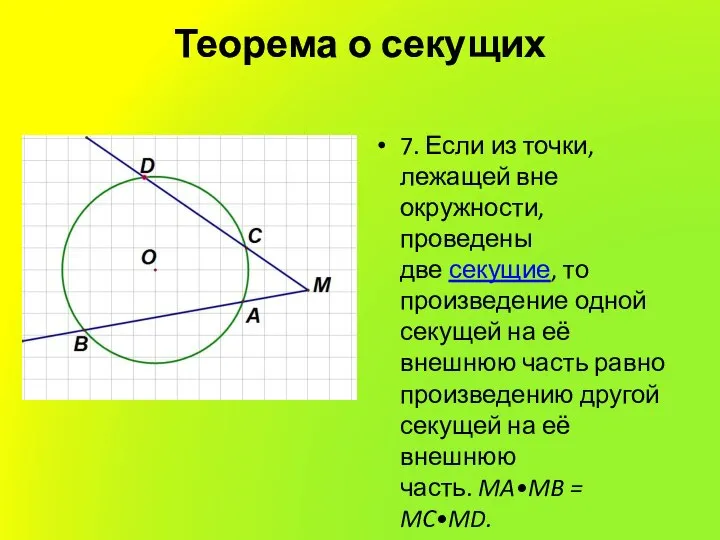
произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.













 Определенный интеграл
Определенный интеграл Комплексные числа и координатная плоскость
Комплексные числа и координатная плоскость Общие методы решения уравнений
Общие методы решения уравнений Погрешности измерительных приборов. Класс точности
Погрешности измерительных приборов. Класс точности Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Умножение дробей
Умножение дробей Применение производной для нахождения наибольших и наименьших значений величин
Применение производной для нахождения наибольших и наименьших значений величин Классическое определение вероятности
Классическое определение вероятности Решение задачи №1 заочного этапа
Решение задачи №1 заочного этапа Многочлены от нескольких переменных
Многочлены от нескольких переменных Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Методика эконометрических исследований
Методика эконометрических исследований Решение задач и примеров
Решение задач и примеров Задачи о теплице. Пример решения
Задачи о теплице. Пример решения Состав чисел. Тренажер в программе PowerPoint
Состав чисел. Тренажер в программе PowerPoint Презентация на тему Цилиндр 11 класс
Презентация на тему Цилиндр 11 класс  Устный счет в пределах 20
Устный счет в пределах 20 Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей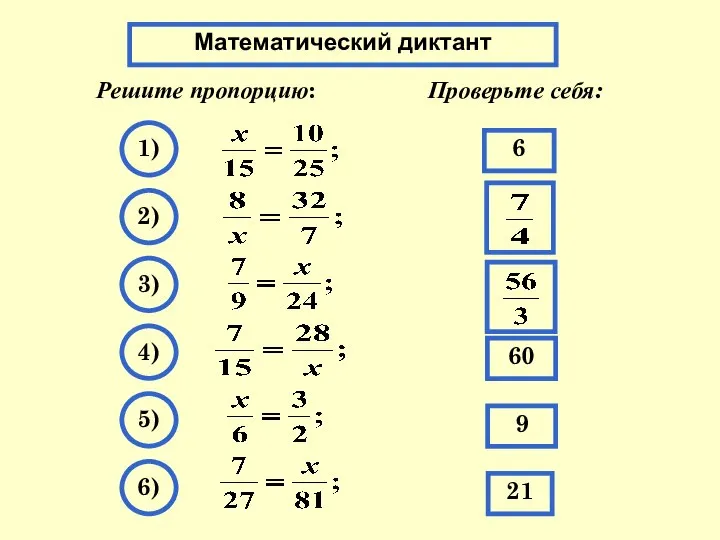 Математический диктант. Решите пропорцию:
Математический диктант. Решите пропорцию: Построение сечений
Построение сечений Дидактические игры на уроках математики
Дидактические игры на уроках математики Мы отправляемся в полёт
Мы отправляемся в полёт Старинные меры длины
Старинные меры длины Подготовка к контрольной работе №4. 5 класс
Подготовка к контрольной работе №4. 5 класс Пирамиды. Объём пирамиды
Пирамиды. Объём пирамиды Приемы быстрого счёта в математике
Приемы быстрого счёта в математике Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)