Содержание
- 2. Предмет изучения Теория игр – раздел теории исследования операций, изучающий формальные модели принятия оптимальных решений в
- 3. ? ! ??!! ???!!! ????!!! !........ Измерить то, что легко измеряемо. Само по себе, это нормально.
- 4. Игровые математические модели имеют широкое практическое применение в экономике, политике, биологии, военном деле и других отраслях
- 5. Основные понятия теории игр Конфликтной называется ситуация, в которой взаимодействует несколько сторон, и при этом каждый
- 6. Черты конфликтной ситуации: наличие заинтересованных сторон наличие своих интересов (целей) у каждой стороны * наличие набора
- 7. Игроки – заинтересованные стороны в игре (участники игры). Парная игра – игра, в которой принимают участие
- 8. Стратегия – любое возможное действие (комплекс действий) игрока Ход - выбор действия игроками (личный ход *)
- 9. Будем предполагать, что каждый из участников парной игры обладает своим набором чистых стратегий: SA={A1,A2,…,Am}, SB={B1,B2,…,Bn} В
- 10. Функция выигрыша – степень удовлетворения интересов игрока (FA). Функция выигрыша определена на множестве ситуаций (SA, SB)
- 11. Предполагается, что игра происходит по определенным правилам (без этого не возможна формализация задачи). Правила - система
- 12. Цель теории игр – выработка рекомендаций для удовлетворительного поведения игроков в конфликте и выявления для каждого
- 13. Замечания: Выбор оптимальной стратегии базируется на принципе разумности каждого игрока, т.е. поведение каждого из них направлено
- 14. Парная игра с нулевой суммой выигрыша Определение. Игры, в которых каждый из игроков преследует противоположные интересы
- 15. Пусть игроки А и В имеют наборы стратегий SA={A 1 A2,…,Am} и SB={B1,B2,…,Bn}. Cитуация Хij=(Ai, Bj)
- 16. Платежная матрица А = Аналогичным образом можно построить матрицу выигрышей игрока В. При этом В= -
- 17. Замечания. Матрица игры существенно зависит от упорядочивания множеств SA и SB. При иной нумерации стратегий матрица
- 18. Пример построения платежной матрицы Задача. Две фирмы А и В производят один и тот же сезонный
- 19. Решение Стороны А и В имеют противоположные интересы. Фирма обладает набором стратегий SA={A1,A2,A3,A4} поставки товара в
- 20. В результате для n = 4 получим матрицу:
- 21. Максиминные и минимаксные стратегии Пусть имеем парную антагонистическую игру между игроками А и В: SA={A1,A2,… ,Am},
- 22. А выберет ту стратегию, при которой показатель эффективности αi принимает максимальное значение: α =max(αi ) =
- 23. Анализ платежной матрицы : игрок В В антагонистической игре результат игры для игрока В удобно анализировать
- 24. Замечание: α и β могут быть любыми действительными числами. Если α Пример. Найти верхнюю и нижнюю
- 25. Уменьшение размерности игры
- 28. Приведение матричной игры к задаче линейного программирования
- 34. Игры с природой
- 38. 5.1.Критерий Бейса относительно выигрышей Показателем эффективности чистой стратегии игрока по критерию Бейса называется среднее значение выигрыша
- 39. 5.2. Критерий Бейса относительно рисков Показателем неэффективности стратегии А относительно рисков называется среднее взвешенное значение рисков
- 41. Решение задачи
- 42. Решение задачи
- 43. Критерии Бейса
- 45. Скачать презентацию


















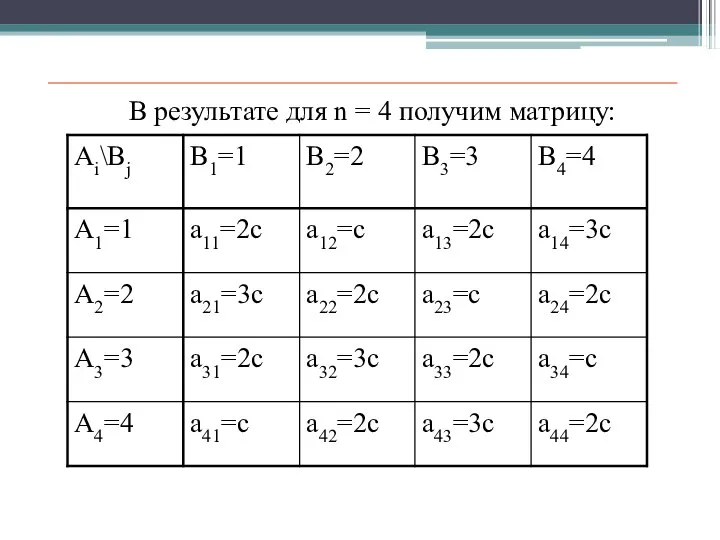



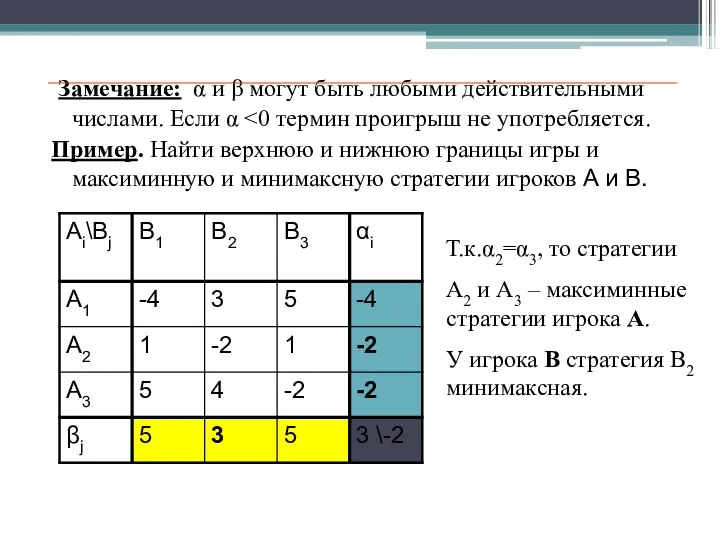













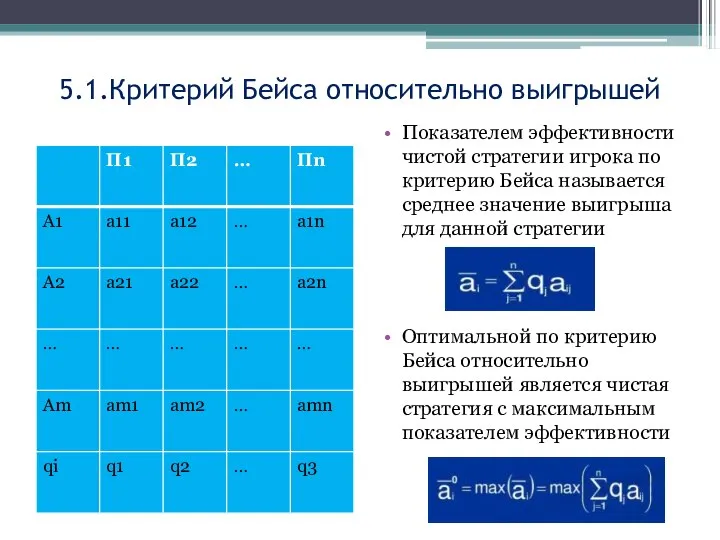

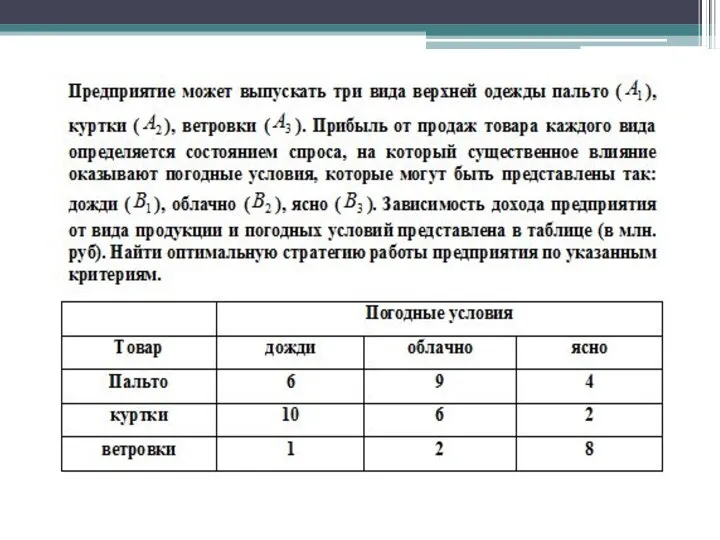
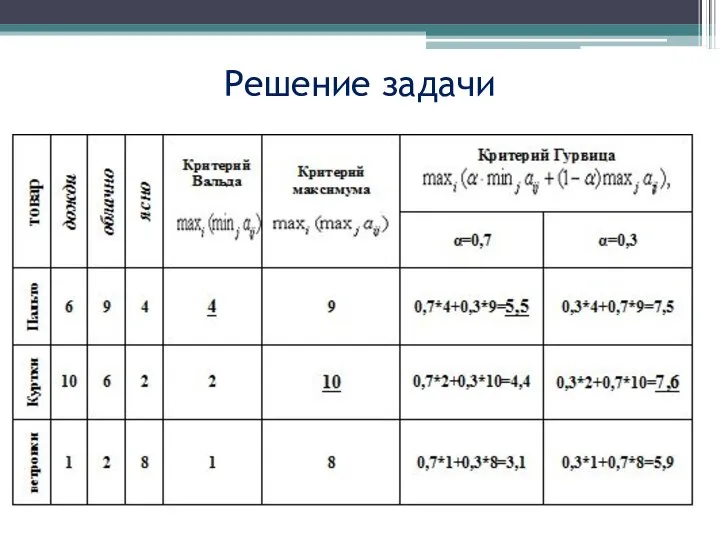
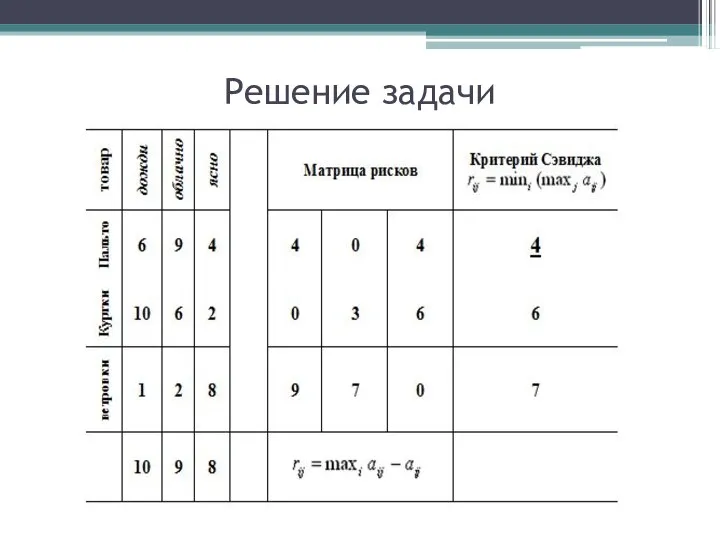
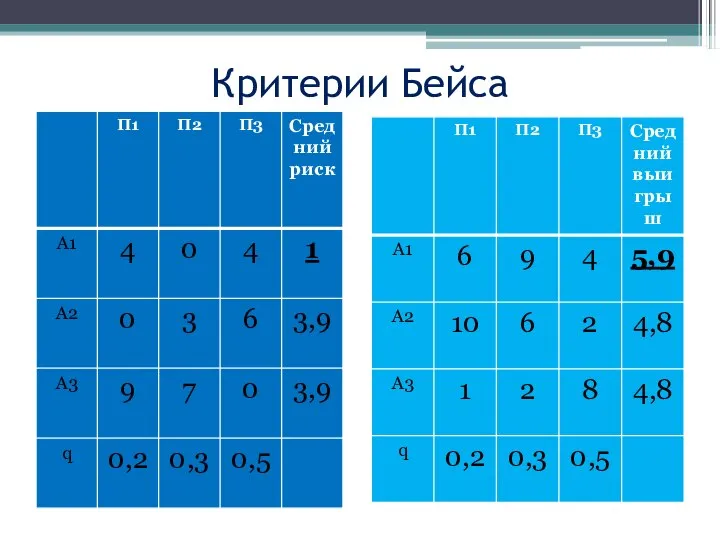
 Таблица сложения
Таблица сложения Группы по одному или нескольким признакам
Группы по одному или нескольким признакам Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Прямоугольный треугольник
Прямоугольный треугольник Презентация на тему Угол между прямыми. Угол между прямой и плоскостью
Презентация на тему Угол между прямыми. Угол между прямой и плоскостью  Перпендикулярности прямой и плоскости
Перпендикулярности прямой и плоскости Интерактивный пазл
Интерактивный пазл Приём вычисления для случаев вида 36+2, 36+20. Задание 1
Приём вычисления для случаев вида 36+2, 36+20. Задание 1 Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Соотношения между тригонометрическими функциями одного и того же аргумента
Соотношения между тригонометрическими функциями одного и того же аргумента Декартова система координат в пространстве
Декартова система координат в пространстве Предел последовательности. Бесконечно убывающая геометрическая прогрессия
Предел последовательности. Бесконечно убывающая геометрическая прогрессия Применение комплексных чисел на практике
Применение комплексных чисел на практике Разные способы нахождения площади многоугольников. Обобщающее повторение при подготовке к ЕГЭ по математике
Разные способы нахождения площади многоугольников. Обобщающее повторение при подготовке к ЕГЭ по математике Ньютон и Лейбниц – создатели математического анализа
Ньютон и Лейбниц – создатели математического анализа Решение уравнений
Решение уравнений Алгебраический способ решения задач (часть 1)
Алгебраический способ решения задач (часть 1) Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования Геометрия вокруг нас
Геометрия вокруг нас Задачи на построение сечений
Задачи на построение сечений Признаки параллельности прямых
Признаки параллельности прямых Обыкновенная дробь. 6 класс
Обыкновенная дробь. 6 класс Мир глазами эколога
Мир глазами эколога Комбинаторика. 11 класс
Комбинаторика. 11 класс Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Кратное сравнение
Кратное сравнение Элективный курс «Математическая статистика и теория вероятностей» Образовательная область «Математика» Лактионова Н.С.
Элективный курс «Математическая статистика и теория вероятностей» Образовательная область «Математика» Лактионова Н.С. 08.09
08.09