Преобразование буквенных выражений. Правила математического синтаксиса

Приступаем к овладению основами буквенного исчисления.
Знакомимся с новыми понятиями и терминами, осваиваем приемы преобразований и принятые способы записи выражений (т. е. некоторые правила математического синтаксиса).
Цель нашего урока
целеполагание
?
буквенное
?
выражение

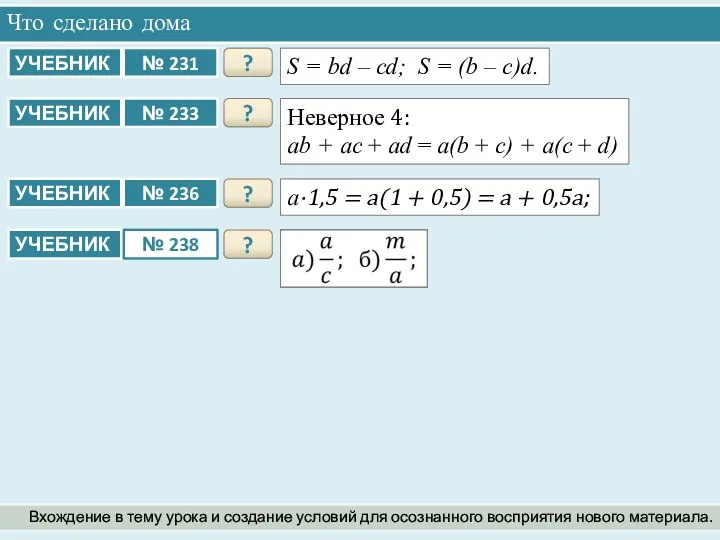
Что сделано дома
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
?
S = bd – cd; S = (b – c)d.
?
Неверное 4:
ab + ac + ad = a(b + c) + a(c + d)
?
a⋅1,5 = a(1 + 0,5) = a + 0,5a;
?

Математическая разминка
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Какие свойства действий позволяют без выполнения вычислений утверждать, что верно равенство:
617 + 238 = 238 + 617;
38⋅(150 + 173) = 38⋅150 + 38⋅173;
315⋅961 = 961⋅315;
Найдите значение выражения и укажите, какие свойства
действий были использованы:
4⋅5,12⋅25;
3,8⋅5,16 – 3,8⋅4,16;
8,8 + 4,5 + 1,1 + 5,5;

Преобразование буквенных выражений
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
a – (b + c ) = a – b – c
Преобразовать буквенное выражение — это значит заменить его другим выражением, принимающим при любых допустимых значениях букв то же значение, что и исходное.
Исходное и преобразованное выражения соединяют знаком «=»
и называют тождественно равными или просто равными.

Преобразование буквенных выражений
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
В любой сумме слагаемые можно как угодно переставлять
и произвольным образом объединять в группы.
В алгебраической сумме слагаемые «путешествуют» вместе со своими знаками.
Из переместительного и сочетательного законов сложения следует правило:
2а - х + Зу = 2а + Зу - х = Зу - х + 2а.
2а - х + Зу
Алгебраическая сумма

Работаем с символами
Практикум
а
a – b – x – y
б
a – b – c + d
в
2a – 2b + 4c – 3d

Работаем с символами
Практикум
Образец:

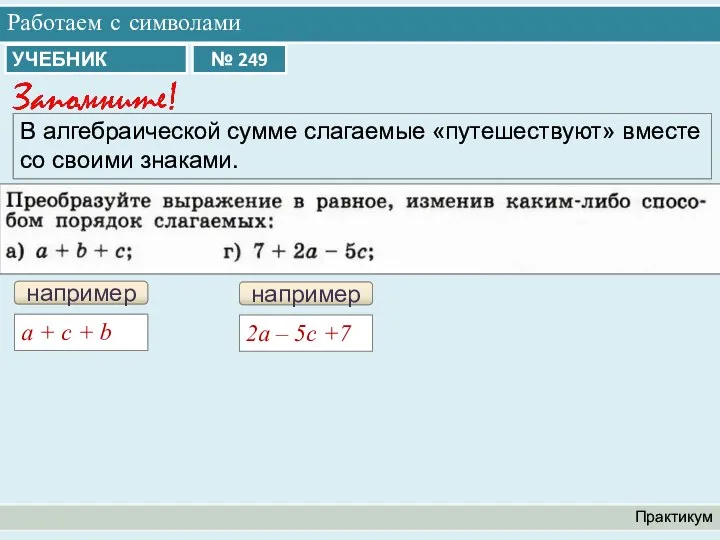
Работаем с символами
Практикум
В алгебраической сумме слагаемые «путешествуют» вместе со своими знаками.
например
a + c + b
например
2a – 5c +7

Преобразование выражений
Практикум
А
6
Учимся заменять сумму одинаковых слагаемых произведением
Б
3
В
2
Г
4

Работаем с моделями
Проверка полученных результатов. Коррекция
а
12х
б
8x + 4y

Преобразование буквенных выражений
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Здесь приведена подробная запись, чтобы показать, как работают
законы алгебры, а на практике промежуточные шаги часто
выполняют устно — слагаемые переставляются и группируются не
руками, а глазами. Например, можно было бы ограничиться такой
цепочкой:
a + b + a - b = 2a + 0 = 2а.

Упростите выражения
Практикум
а
m – 12
б
x – 12
в
a
г
9 – b
а
2b
б
x – z
в
5
г
3x
д
2x
е
3a – 3

Самостоятельная работа
Проверка полученных результатов. Коррекция