ریاضی جزوه کامل

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.دنیوگ یم هعومجم )یرارکت ریغ( زیامتم ود هب ود و صخشم لاماک ءایشا زا یا هتسد هب : هعومجم
؟تسا هعومجم کی هدننک صخشم ریز تارابع زا کی مادک : لاثم
)تسا هعومجم( 01 زا رتمک لوا دادعا )ج )تسین هعومجم( ابیز لگ 4 )ب )تسین هعومجم( یلاوتم جوز ددع 3 )فلا
.دننک یم یراذگ مان یسیلگنا گرزب فورح اب ار هعومجم و دنهد یم ناشن { } دلاوکآ تروص هب ار هعومجم : هتکن
تروص هب ندوبن وضع تملاع و ∈ تروص هب ندوب وضع تملاع و دنیوگ یم وضع هعومجم لخاد ترابع و دادعا زا کی ره هب : هتکن
.دشاب یم ∉
.دنهد یم ناشن ?(?) تروص هب ار ? دننام هعومجم ره یاه وضع دادعت : هتکن
.دشاب یم ∅ ای { } تروص هب یهت هعومجم تملاع .دشابن یوضع چیه یاراد هک یا هعومجم : یهت هعومجم
رفص زا رتمک حیحص دادعا )ب 4 زا رتمک یعیبط دادعا )فلا
هعومجم رد ? هعومجم وضع ره و ? هعومجم رد ? هعومجم وضع ره هک دنیوگ یم ربارب ار ? و ? هعومجم ود : ربارب هعومجم ود
: لباقم ی هعومجم ود دننام .دشاب هتشاد دوجو ?
: تسا رارقرب هراومه لباقم یاه هطبار هاگنآ دشاب ? ⊆ ? رگا : هتکن
ار وضع دادعت و میشاب هتشاد ار هعومجم ریز دادعت رگا .مینک یم هدافتسا 2? هطبار زا اه هعومجم ریز دادعت ندرک ادیپ یارب : هتکن
.مینک یم هیزجت ار هدش هداد ددع دنشاب هتساوخ
؟دراد هعومجم ریز دنچ ? = {1 , 2 , … , 11} ی هعومجم )فلا : لاثم
؟تسا وضع دنچ یاراد هعومجم نیا .تسا هعومجم ریز 33 یاراد هعومجم کی )ب
? = {3 , {4 , 5} , 6}
.دینک صخشم ار ترابع ره یتسردان ای یتسرد ? ی هعومجم هب هجوت اب : لاثم
?(?) = 4 ✗ 3 ∈ ? ✓ 4 ∉ ? ✓ {6} ∈ ? ✗
؟تسا یهت هعومجم ریز یاه هعومجم زا کی مادک : لاثم
{1 , 2 , 3}
{000 , −3 , −2 , −1}
{ }
5 و 4 نیب یعیبط دادعا )ج
5
20
? = {4 , 3 , 1} و ? = {√9 , 70 , }
؟دیروآ تسد هب ار ? و ? رادقم .دنربارب ریز ی هعومجم ود : لاثم
{? − 7 , 3} = {4 , ?} ? − 7 = 4 ⇒ ? = 11 , ? = 3
? ⊆ ? تروص هب ار نآ و دشاب ? هعومجم زا یوضع ? هعومجم وضع ره هاگ ره تسا ? هعومجم ریز ? هعومجم : هعومجم ریز
.دنهد یم ناشن ? ⊆ ? تروص هب ار نآ دشابن ? هعومجم ریز ? رگا .دنهد یم ناشن
? 10
?(?) = 10 ⇒ 2 = 2 = 1024 هعومجم ریز
32 = 25 ⇒ دراد وضع 5
A ∪ B = B و ? ∩ ? = ?
)لوا لصف(
اه هعومجم
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
: درف یعیبط دادعا هعومجم )ه
: تسا ریز تروص هب یضایر دادعا هعومجم نو رادومن : هتکن
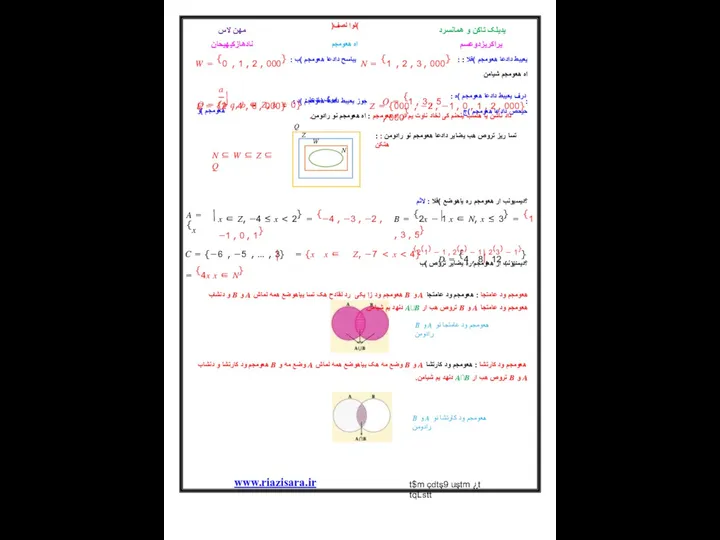
هعومجم ود کارتشا و دنشاب ? وضع مه و ? وضع مه هک ییاهوضع همه لماش ? و ? هعومجم ود کارتشا : هعومجم ود کارتشا
.دنهد یم شیامن ?⋂? تروص هب ار ? و ?
? = {0 , 1 , 2 , 000} : یباسح دادعا هعومجم )ب ? = {1 , 2 , 3 , 000} : یعیبط دادعا هعومجم )فلا : اه هعومجم شیامن
? = {2 , 4 , 6 , 000} : جوز یعیبط دادعا هعومجم )د ? = {000 , −2 , −1 , 0 , 1 , 2 , 000}: حیحص دادعا هعومجم )ج
? = {1 , 3 , 5 , 000}
?
? = {? ?, ? ∈ ?, ? ≠ 0} : ایوگ دادعا هعومجم )و
? ⊆ ? ⊆ ? ⊆ ?
?
?
?
.داد ناشن یا هتسب ینحنم کی لخاد ناوت یم ار اه هعومجم : اه هعومجم نو رادومن
?
? = {?
? ∈ ?, −4 ≤ ? < 2} = {−4 , −3 , −2 , −1 , 0 , 1}
؟دیسیونب ار هعومجم ره یاهوضع )فلا : لاثم
? = {2? − 1 ? ∈ ?, ? ≤ 3} = {1 , 3 , 5}
{2(1) − 1 , 2(2) − 1 , 2(3) − 1}
؟دیسیونب ار هعومجم ره یضایر تروص )ب
? و ? هعومجم ود عامتجا نو رادومن
? و ? هعومجم ود کارتشا نو رادومن
? = {−6 , −5 , … , 3} = {? ? ∈ ?, −7 < ? < 4} ? = {4 , 8 , 12 , … } = {4? ? ∈ ?}
و دنشاب ? و ? هعومجم ود زا یکی رد لقادح هک تسا ییاهوضع همه لماش ? و ? هعومجم ود عامتجا : هعومجم ود عامتجا
.دنهد یم شیامن ?⋃? تروص هب ار ? و ? هعومجم ود عامتجا
)لوا لصف(
اه هعومجم
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
? هعومجم وضع یلو دنشاب ? هعومجم وضع هک تسا ییاهوضع همه لماش ) ? یاهنم ?( ? − ? هعومجم : هعومجم ود لضافت
.دنشابن
؟دیسیونب
؟دیروآ تسد هب ار ریز یاه لامتحا سات کی باترپ رد : لاثم
؟دیروآ تسد هب ار ریز یاه لامتحا سات ود باترپ رد : لاثم
: دیایب 3 زا رتکچوک ددع مود سات و درف ددع لوا سات هک نیا ندمآ لامتحا )فلا
: دوش 6 سات ددع ود ره عومجم هک نیا ندمآ لامتحا )ب
? = {−1 , 0 , 1 , 2}
ار هعومجم ره یاهوضع .دشاب ? = {?2 + 1 ? ∈ ?} و ? = {? ? ∈ ?, −2 < ? ≤ 2} و ? = {1 , 2 , 3} هعومجم رگا : لاثم
? = {12 + 1 , 22 + 1 , 32 + 1} = {2 , 5 , 10 }
فلا) ? − ? = {1 , 3}
ب) ? ∩ (? ∪ ?) = {−1 , 0 , 1 , 2 } ∩ {1 , 2 , 3 , 5 , 10} = {1 , 2}
؟دینزب روشاه ار هدش هداد یاه هعومجم لکش ره هب هجوت اب : لاثم
A
B
C
(A⋂B) ∪ ?
(A ∪ C) − ?
: مینک یم هدافتسا ریز ی هطبار زا دماشیپ ره لامتحا ندروآ تسد هب یارب : لامتحا و هعومجم
بولطم یاه تلاح دادعت
نکمم یاه تلاح ی همه دادعت
دماشیپ نداد خر لامتحا = ⇒ ?(?)
?(?)
= ?(?)
?(?) = =
3 1
6 2
?(?) = 2 = 1
: 5 یواسم و رتگرزب ددع ندمآ لامتحا )ب
6 3
? = {2 , 3 , 5 }
: لوا ددع ندمآ لامتحا )فلا
? = {5 , 6}
?(?) = 62 = 36
اه تلاح لک
6 1
? = {(1 , 1) , (1 , 2) , (3 , 1) , (3 , 2) , (5 , 1), (5 , 2)} ⇒ ?(?) = 6 ⇒ ?(?) = =
36 6
5
? = {(1 , 5) , (5 , 1) , (2 , 4) , (4 , 2) , (3 , 3)} ⇒ ?(?) = 5 ⇒ ?(?) =
36
A B C A
B C
A
B
C
? و ? هعومجم ود لضافت نو رادومن
)لوا لصف(
اه هعومجم
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
)دشاب رفص فلاخم جرخم و حیحص ددع جرخم و تروص( .دراد مان ایوگ ددع دوش لیدبت رسک هب هک یددع ره : ایوگ دادعا
: دنهد یم شیامن ? یسیلگنا فرح اب ار ایوگ دادعا : هتکن
.تسا اه جرخم )م .م . ب( نامه کرتشم جرخم نیرتهب هک هتفرگ کرتشم جرخم : یرسک دادعا قیرفت و عمج
: دننام
رد اه جرخم و مه رد اه تروص سپس .درک هداس جرخم اب ار تروص نداد باوج زا لبق ناوت یم برض رد طقف : یرسک دادعا برض
.دوش یم برض مه
: دننام
)دوش یم برض یمود رسک سوکعم رد یلوا رسک( .دوش یم لیدبت برض هب میسقت : یرسک دادعا میسقت
: دننام
؟دیروآ تسد هب ار ریز ترابع لصاح : لاثم
: درک هدافتسا ناوت یم شور ود زا : اهرسک هسیاقم
.مینک یم هسیاقم ار اهرسک سپس هدرک ربارب ار اهرسک مامت جرخم ادتبا : اهرسک ندرک جرخم مه )فلا
.دینک بترم گرزب هب کچوک زا ار ریز یاهرسک : لاثم
).میهد یم همادا راشعا مقر ود ات تمسق جراخ و میسقت جرخم رب تروص( : راشعا ددع هب لیدبت )ب
.دینک بترم گرزب هب کچوک زا ار ریز یاهرسک : لاثم
.دراد دوجو ایوگ ددع تیاهن یب ایوگ ددع ود ره نیب )هتکن
?
Q = {? ? , ? ∈ ?, ? ≠ 0}
21 21 63 63
(− 5 ) − (− 7 ) = −25 + 21 = − 2 اه جرخم (م . م . ب) ⇒ (21 , 21 ) = 63
5 6
21 20
(− ) × (− ) = +
2
1
2
2
1
1
7
12
7
5
(+ ) ÷ (− ) = (+ ) × (− ) = −
= −1
1
5
2
1 5 1 12 6 21
5
1
6
2
25
6
5
1
6
(+ ) ÷ [(− ) + (+ )] = (+ ) ÷ (
−2 + 9
25
1
) = (+ ) × (+ ) = + = = 2
25 20 5 2
6 1 1 1 1
2
+1
5
, , ⇒ , , , ⇒ < < <
1 , 6 2 7 1 25 20 21 1 2 7 6
5 1 1 20 10 10 10 10 5 1 20 1
(1 , 1 , 5 , 20) = 10
1 , 6 2 7 1
5 1 1 20 5
, , ⇒ = 0/10 ,
6
1
= 0/75
2
1
, = 0/50
,
= 0/70
7 ⇒ 1 < 2 < 7 < 6
20 5 1 20 1
)مود لصف(
یقیقح یاهددع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
: تسا ریز تروص هب نآ یدربراک شور ود هک دراد دوجو شور دنچ : یرسک ددع ود نیب ییاه رسک ندرک ادیپ
دحاو کی رد ار جرخم و تروص سپس هتفرگ کرتشم جرخم ادتبا )3 مینک یم عمج مه اب اه جرخم و مه اب اه تروص )0
.مینک برض هدش هتساوخ دادعت زا رتشیب
1 6
5 1
؟دیسیونب ایوگ ددع ود و نیب : لاثم
: یراشعا دادعا هب رسک لیدبت
.دراد مان موتخم ار رسک نآ دوش رفص رسک جرخم رب تروص هدنامیقاب رگا : موتخم ای یهانتم یراشعا یاهددع )0
: دننام
.تسا موتخم رسک نآ دنشاب 5 و 3 لماع رسک جرخم هیزجت رد رگا : هتکن
: دننام
بوانتم ار نآ دوش رارکت بترم یددع تمسق جراخ رد رسک جرخم رب تروص میسقت رد رگا : هداس بوانتم یراشعا یاهددع )3
.دنیوگ یم هداس
)تسا ددع شدرگ ای رارکت ینعم هب ددع یور هریت طخ( : دننام
.تسا هداس بوانتم رسک نآ دنشابن 5 و 3 لماع رسک جرخم هیزجت رد رگا : هتکن
: دننام
هب راشعا مقر دنچ ای کی زا دعب تمسق جراخ رد رسک جرخم رب تروص میسقت رد رگا : بکرم بوانتم یراشعا یاه ددع )3
.دنیوگ یم بکرم بوانتم رسک نآ هب دنسرب یرارکت یاه مقر
: دننام
.تسا بکرم بوانتم رسک نآ دنشاب یرگید لماع 5 و 3 لماع زا ریغ رسک جرخم هیزجت رد رگا : هتکن
: دننام
6 7
< < <
22 1
1 9 21 5
6
و ⇒ و ⇒ و ⇒ < < <
1 25 23 15 11 15 13 17 11
1 5 10 10 30 30 30 30 30 30
لوا شور
مود شور
6 = 0/75
1 5
3
و = 2/1
6
10
10 = 11 × 5 و
5
1
1 = 1
6
5 = 0/1515000 = 0/̅1̅̅5̅ و 2 = 0/66000 = 0/6̅
22 6
6
77
77 = 7 × 22 و
3
26
5 = 0/166000 = 0/16̅ و
3 11
7 = 0/62121000 = 0/62̅̅1̅
5 21
21 = 1 × 7 و
1 75
75 = 6 × 5
1
)مود لصف(
یقیقح یاهددع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.دنراد مان گنگ دادعا دنشابن بوانت هرود یاراد و یهانتم ان اه نآ یراشعا ماقرا دادعت هک دادعا : مصا ای گنگ دادعا
.دنهد یم ناشن ?? ای ?́ یسیلگنا فرح اب ار گنگ دادعا هعومجم : هتکن
)دنتسه گنگ ددع دنرادن قیقد رذج هک یدادعا ینعی(.تسا گنگ یددع √? هاگنآ دشابن لماک عبرم ? رگا : هتکن
) π ≃ 6/2125913565 : راشعا مقر 20 ات π ددع ( .تسا گنگ ددع تسین بوانت هرود یاراد نوچ ? ددع : هتکن
5
?́
?́
√17
?́
.دراد دوجو گنگ ددع تیاهن یب ددع ود نیب : هتکن
.دیسیونب گنگ ددع ود هدش هداد ددع ود ره نیب : لاثم
√1 و √6 )فلا
6 و 1 )ب
دراد رارق -0 و 1 نیب
.دیهد شیامن دادعا روحم یور ار 2 − √5 و √27 دادعا : لاثم
: دهد یم لیکشت ار یقیقح دادعا هعومجم گنگ دادعا و ایوگ دادعا هعومجم عامتجا : یقیقح دادعا
.دنهد یم ناشن ? یسیلگنا فرح اب ار یقیقح دادعا هعومجم : هتکن
(?́ ) گنگ دادعا و (?) ایوگ دادعا و (?) حیحص دادعا و (?) یباسح دادعا و (?) یعیبط دادعا هعومجم نو رادومن : هتکن
: تسا ریز تروص هب (?) یقیقح دادعا و
1 − √2 ∈ ?́
? ∈
∈ ?́
− 1 ∉
∉
6/21 ∉ ?́
0/6
√0/63
تسین لماک عبرم 44
.دیهد رارق ∉ ای ∈ تملاع یلاخ یاج رد : لاثم
تسین لماک عبرم 3
√6 < √6/2 < √6/1 < √1
1 = √1 < √5 < √3 < √9 = 6
6 − √23 < 6 − √20 < 6 − √9 ⇒ −2 < 6 − √20 < 0
0
1
√17
0
1
√5
Q ∪ ?́ = ?
Q́
N
W
Z
R
Q
N ⊆ W ⊆ Z ⊆ Q ⊆ R
, ?́ ⊆ ?
.دراد رارق یلاوتم حیحص ددع ود مادک نیب 6 − √20 ددع : لاثم 6
1
)مود لصف(
یقیقح یاهددع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
طخ کی تروص هب دادعا نیا شیامن سپ دنتسه گنگ و ایوگ دادعا لماش یقیقح دادعا نوچ : روحم یور یقیقح دادعا شیامن
)میهد یم رارق یلاخ وت هریاد شکرس نودب و رپوت هریاد دشاب هتشاد شکرس یواسمان تملاع رگا( تسا یدتمم
.میهد یم ناشن |?| تروص هب ار نآ و میمان یم ? قلطمردق تاصتخم ادبم زا ار ? دننام ددع کی شیامن هطقن ی هلصاف : قلطمردق
: ددع نآ دوخ اب تسا ربارب تبثم ددع قلطم ردق )فلا : قلطم ردق صاوخ
: تسا رفص اب ربارب رفص قلطم ردق )ب
: تسا ددع نآ هنیرق اب ربارب یفنم ددع قلطم ردق )ج
.دیسیونب قلطم ردق دامن زا هدافتسا نودب ار ریز یاه ترابع : لاثم
6
2 1
1
.دیروآ تسد هب ار ریز ترابع لصاح .دشاب ? = − و ? = 6 و ? = رگا : لاثم
: تسا رارقرب لباقم هطبار هراومه قلطم ردق موهفم هب هجوت اب : هتکن
.دیروآ تسد هب ار ترابع ره لصاح : لاثم
A = {? ∈ ?
− 1 ≤ ? < 6}
.دیهد ناشن روحم یور ار ریز دادعا هعومجم : لاثم
B = {? ∈ ? 2 ≤ ?}
0
1 2
3
−3 −2 −1
0
1 2 3
−3 −2 −1
0
−3 −2 −1 1 2 3
.دیسیونب ار لباقم روحم رظانتم هعومجم : لاثم
C = {? ∈ ? − 6 < ? < 6}
? > 0 ⇒ |?| = ?
? = 0 ⇒ |?| = 0
? < 0 ⇒ |?| = −?
|1 − 3 × 11 ÷ 6 + 1| = |−1| = 1
1
6 1
|−3? − 1?| + 1|?| = |−3 ( ) − 1 (− 2)| + 1|6| = |−1 + 1| + 1(6) = 1 + 3 = 1
√?1 = |?|
√1
1
√(1 − √5) = |1 − √5| = − (1 − √5) = √5 − 1
یفنم لصاح
√21 √1
√(6√1 − 1√1 1 = |6√1 − 1√1| = 6√1 − 1√1
)
تبثم لصاح
1
−11
−1
√9
|6 − √1| = 6 − √1
تبثم لصاح
|?10 − ?60| = ?60 − ?10
یفنم لصاح
)مود لصف(
یقیقح یاهددع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
دن رگیدکی فصنم دومع اه رطق عبرم رد ⟸
.تسا هدوبن صخشم ادتبا رد هک یعوضوم ندش مولعم یارب یلبق تامولعم زا هدافتسا و ندروآ لیلد : للادتسا
.مییوگ یم تابثا دهد هجیتن یتسرد هب ار رظن دروم عوضوم هک یللادتسا هب : تابثا
.مینک یم هدافتسا ضقن لاثم زا یضایر یاعدا کی در یارب : ضقن لاثم
دوجو لکش نآ رد دید یاطخ تسا نکمم اریز درک هدافتسا دوهش ای لکش مسر زا ناوت یمن هلئسم کی تابثا یارب هراومه : هتکن
.دشاب هتشاد
: دینزب ضقن لاثم کی ریز یاه هلئسم زا کی ره یارب : لاثم
.تسین هیواز و هشوگ یاراد هک تسا یسدنه لکش کی هریاد ؟دنراد هیواز ای هشوگ یسدنه لاکشا مامت )فلا
.تسا زین لوا هک تسا یجوز ددع اهنت 3 ددع ؟دنتسه لوا جوز دادعا مامت )ب
: تسا یقطنم ریغ مادک و یقطنم ریز یاه للادتسا زا کی مادک : لاثم یقطنم ریغ ؟دنک یم لاوس نم زا ملعم زور نامه مدناوخن سرد نم تقو ره : دیوگ یم یلع )فلا یقطنم ؟دشاب نیشام ینف ضقن لیلد هب تسا نکمم اهداج رد گرم هب رجنم فداصت )ب
)هلئسم اه هداد هصلاخ روط هب( .دشاب هلئسم نآ هب طوبرم هک یقیاقح ای هدش هداد هلئسم رد هک یتاعلاطا : هلئسم ضرف
.دنیوگ یم هلئسم مکح ار هلئسم یاه هتساوخ : هلئسم مکح
: دینک صخشم ار مکح و ضرف هلئسم ره رد : لاثم
ور هب ور یاه هیواز ندوب ربارب : مکح یزول صاوخ : ضرف .دنربارب یزول ور هبور یاه هیواز )فلا سامم ود ندوب ربارب : مکح عاعش رب سامم طخ ندوب دومع و هریاد : ضرف .دنربارب هراومه هریاد رد سامم ود لوط )ب
: دیسیونب ار لصاح هجیتن هدش هداد تاضورفم هب هجوت اب : لاثم
دن رگیدکی فصنم دومع اه رطق یزول رد
تسا عبرم یعون یزول
} )فلا
تسا لیطتسم یعون عبرم ⟸
تسا لیطتسم دشاب هتشاد همئاق هیواز هک یعلض راهچ ره
} )ب
تسا همئاق هیواز یاراد عبرم
)موس لصف(
هسدنه رد تابثا و للادتسا
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

مهن لاس
نادهازکیهیحان
: دنتسه تشهن مه تلاح هس هب ثلثم ود : اه ثلثم یتشهن مه
)ض ض ض( یواسم علض هس )ج )ز ض ز( یواسم نیب علض و یواسم هیواز ود )ب )ض ز ض( یواسم نیب هیواز و یواسم علض ود )فلا
.تسین یتشهن مه یاه تلاح زا )ز ز ز( یواسم هیواز هس : هتکن
: دنتسه تشهن مه تلاح ود هب هیوازلا مئاق ثلثم ود : هیوازلا مئاق ثلثم ود یتشهن مه
)ض و( علض کی و رتو )ب )ز و( دنت ی هیواز کی و رتو )فلا
: ثلثم ود یتشهن مه هرابرد یتاکن
.دنتسه کرتشم علض یاراد دنشاب هدیبسچ مه هب ثلثم ود رگا )فلا
.دنتسه سار هب لباقتم هیواز یاراد دنشاب یردبرض تروص هب ثلثم ود رگا )ب
.مینک یم هدافتسا هریاد عاعش یربارب زا دنشاب هریاد لخاد ثلثم ود رگا )ج
.دنربارب هیواز هس ره و علض هس ره علاضلاا یواستم ثلثم رد )د
.دنربارب هدعاق رواجم ی هیواز ود و قاس ود نیقاسلا یواستم ثلثم رد )ه
.دنربارب رظانتم یاه هیواز و علاضا تشهن مه ثلثم ود رد : هتکن
؟دینک صخشم ار لوهجم ریداقم .دنتسه تشهن مه ریز ثلثم ود : لاثم
)دنربارب رظانتم یاه هیواز و علاضا تشهن مه ثلثم ود رد(
A
B
C
?
1
2
{
?̂1 + ?̂2 = 181 هجرد
?̂1 + ?̂ + ?̂ = 181 هجرد
} ⟹ ?̂1 + ?̂2 = ?̂1 + ?̂ + ?̂ ⟹ ?̂2 = ?̂ + ?̂
2
O 1
3
?1 + ?2 = 181 هجرد
{
?̂2 + ?̂3 = 181 هجرد
} ⟹ ?1̂ + ?2̂ = ?2̂ + ?3̂ ⟹ ?1̂ = ?3̂
یدیلک تاکن و همانسرد
یراکریزدوعسم
.دنربارب مه اب سار هب لباقتم یاه هیواز دینک تباث : لاثم
سار هب لباقتم هیواز ود ?̂3 و ?̂1 : ضرف
?̂1 = ?̂3 : مکح
̂ ̂
.نآ رواجم ریغ یلخاد ی هیواز ود عومجم اب تسا ربارب ثلثم یجراخ ی هیواز دینک تباث : لاثم
?̂2 = ?̂ + ?̂ : مکح ثلثم یجراخ ی هیواز ?̂2 : ضرف
65
?
14
85
y
12
180 − (85 + 65) = 30 )تسا هجرد 081 ثلثم یلخاد یاه هیواز عوجم(
? = 30 , ? = 14
)موس لصف(
هسدنه رد تابثا و للادتسا
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
هلئسم لح دربهار )4 هلئسم مکح و ضرف نتشون )3 لکش مسر )3 هلئسم مهف و کرد )0
.تسا هزادنا کی هب طخ هراپ رس ود زا دشاب هتشاد رارق فصنم دومع یور هطقن ره دیهد ناشن : لاثم
.دنک فصن ار طخ نآ و دشاب دومع هدش مسر طخ رب یطخ فصنمدومع )هلئسم مهف و کرد( : لوا ماگ
)مکح و ضرف نتشون( : موس ماگ )لکش مسر( : مود ماگ
)هلئسم لح دربهار(: مراهچ ماگ
.دنتسه ربارب مه اب هریاد جراخ هطقن زا هدش مسر سامم ود لوط دیهد ناشن : لاثم
)مکح و ضرف نتشون( : موس ماگ )لکش مسر( : مود ماگ
)هلئسم لح دربهار( : مراهچ ماگ
A
B
C
M
?? = ?? ضرف
?? = ?? ضرف
?? = ?? = کرتشم علض
}
⟹ ??? ≅ ???
(ض ض ض)
.دیسیونب ار ??? و ??? ثلثم ود یتشهن مه لیلد .دنتسه نیقاسلا یواستم ??? و ??? ثلثم ود ریز لکش رد : لاثم
??? ≅ ??? : مکح ?? = ?? , ?? = ?? : ضرف
?
B
A H
.دنک یم فصن ار رتو نآ دوش یم دومع رتو رب هریاد زکرم زا هک یطخ دیهد ناشن ریز لکش هب هجوت اب : لاثم
?? = ?? : مکح ?? رب دومع ?? و هریاد زکرم ? : ضرف
?? = ?? هریاد عاعش
? = ? = 0 هجرد }
1 2
?? = ?? = کرتشم علض
⟹ ??? ≅ ??? ⟹ ?? = ??
(ض و) ( رظانتم یازجا)
: تسا زاین )مدق( ماگ 4 هلئسم لح یارب : هلئسم لح یاه مدق
فصنم دومع ?? : ضرف
?? = ?? : مکح
?? = ?? ضرف
? = ? = 0 هجرد
1 2
?? = ?? = کرتشم علض
} ⟹ ??? ≅ ??? ⟹ ?? = ??
(ض ز ض) ( رظانتم یازجا)
A
?
O
H
?? = ?? , ?̂ = ?̂ = 01 : ضرف
?? = ?? : مکح
O
.دنربارب مه اب عاعش ود هریاد رد و دومع سامم طخرب هریاد عاعش )هلئسم مهف و کرد( : لوا ماگ
A
B
M
?? = ?? هریاد عاعش
?̂ = ?̂ = 0 هجرد }
?? = ?? = کرتشم علض
⟹ ??? ≅ ??? ⟹ ?? = ??
(ض و) ( رظانتم یازجا)
)موس لصف(
هسدنه رد تابثا و للادتسا
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.دیروآ تسد هب ار ? و ? رادقم )فلا
؟تسا رتم ولیک دنچ هداج یعقاو لوط )فلا
؟تسا هجرد دنچ تیعقاو رد هیواز نیا هزادنا دشاب هجرد 41 هشقن یور یاه هیواز زا یکی ی هزادنا رگا )ب
.تسا هجرد 41 زین تیعقاو رد هیواز سپ .دنک یمن رییغت هیواز هباشتم لکش ود رد
.تسا ربارب هباشت تبسن اب هنایم و فصنم دومع و زاسمین و عافترا و طیحم تبسن )فلا : هباشتم ثلثم ود رد : هتکن
.تسا ربارب هباشت تبسن روذجم اب تحاسم تبسن )ب
3
5
: دشاب یم ثلثم ود هباشت تبسن : لاثم
دشاب هدرکن رییغت اه هیواز یلو )رییغت نودب ای گرزب ای کچوک( دنک رییغت تبسن کی هب علاضا هک یلکش ود : هباشتم لکش ود
.دنیوگ یم هباشتم لکش ود
.دنتسه هباشتم هراومه علاضلاا یواستم ثلثم ود و هاوخلد عبرم ود : هتکن
)دنکن رییغت هزادنا کی هب تسا نکمم علاضا نوچ( .تسین هباشتم هراومه لیطتسم ود : هتکن
)دنشابن ربارب ود هب ود اه هیواز تسا نکمم نوچ( .تسین هباشتم هراومه هاوخلد یزول ود : هتکن
.دنیوگ یم هباشت تبسن ار هباشتم لکش ود رظانتم علاضا تبسن : هتکن
.تسا کی ددع اه نآ هباشت تبسن و هباشتم هراومه تشهن مه لکش ود : هتکن
یاه هزادنا هب ??? ثلثم علاضا و 6 و 4 و 3 یاه هزادنا هب ??? ثلثم علاضا رگا .دنتسه هباشتم ??? و ??? ثلثم ود : لاثم
)دنا هدش هتشون گرزب هب کچوک زا ثلثم ود علاضا( : دنشاب ? − 3 , 8 , 2?
= =
3 4 6
2? 8 ? − 3
⟹
2? 8
3 = 4 ⟹ 8? = 24 ⟹ ? = 3
4 6
علاضا بسانت
{8 = ? − 3 ⟹ 4? − 12 = 48 ⟹ 4? = 61 ⟹ ? = 15
4 = 1 .دیسیونب ار ثلثم ود هباشت تبسن )ب
8 2
: دشاب رتم یتناس 03 هشقن نیا یور یا هداج لوط رگا .تسا 1: 111111 یا هشقن سایقم : لاثم
1 12
111111 ?
= ⟹ ? = 1211111??
1211111 ÷ 111111 = 12??
تسا رتم یتناس 011111 رتم ولیک ره : دحاو لیدبت
؟تسا دنچ ثلثم ود هنایم تبسن )فلا
3
5
؟تسا دنچ ثلثم ود تحاسم تبسن )ب
3
2
( ) =
5
9 25
)موس لصف(
هسدنه رد تابثا و للادتسا
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.دوش یم هدافتسا ناوت زا یسیون هصلاخ یارب دوش برض شدوخ رد راب دنچ یددع رگا : ناوت
: دننام
: دننام
.مینک یم برض مه رد ار اه هیاپ و هتشون ار اه ناوت زا یکی : دنشاب ربارب اه ناوت رگا )ب
: دننام
.مینک یم مک مه زا ار اه ناوت و هتشون ار اه هیاپ زا یکی : دنشاب ربارب اه هیاپ رگا )فلا : راد ناوت دادعا میسقت
: دننام
.مینک یم میسقت مه رب ار اه هیاپ و هتشون ار اه ناوت زا یکی : دنشاب ربارب اه ناوت رگا )ب
: دننام
.مینک یم هدافتسا هیزجت زا دنشابن ربارب اه ناوت و اه هیاپ راد ناوت دادعا میسقت و برض رد رگا : هتکن
: دننام
: دننام
.دوش لیدبت تبثم ناوت هب ات هدرک سوکعم ار هیاپ ددع یفنم ناوت ندروآ تسد هب یارب : یفنم ناوت
?
?
?−? = ( )
?
.دنک یم قدص یفنم ناوت اب دادعا یارب راد ناوت دادعا دعاوق مامت : هتکن
.دوش یم هنیرق نآ ناوت دوش هداد لاقتنا تروص هب جرخم زا ای و جرخم هب تروص زا )رفص زا ریغ( یحیحص ددع رگا : هتکن
.دیسیونب )تبثم ناوت( یعیبط ناوت تروص هب ار ترابع ره لصاح : لاثم
4 × 4 × 4 = 43
? × ? × … × ? = ??
ناوت
هیاپ
راب ?
.مینک یم عمج مه اب ار اه ناوت و هتشون ار اه هیاپ زا یکی : دنشاب ربارب اه هیاپ رگا )فلا : راد ناوت دادعا برض
?? × ?? = ??+?
47 × 43 = 410
?? × ?? = (??)?
127 × 37 = 367
?? ÷ ?? = ??−?
93
95 =
9
2
?
?? ÷ ?? = (?)
?
208 ÷ 48 = 58
26 + 26 = 2 × 26 = 27
48 × 23 = (22)8 × 23 = 219
هیزجت
92 ÷ 27 = (32)2 ÷ 33 = 3
هیزجت
.مینک یم برض هب لیدبت ار ترابع نآ دشاب عمج تملاع اه نآ نیب و دنشاب مه لثم راد ناوت دادعا رگا : هتکن
216
34
310
95 + 95 + 95 = 3 × 95 = 3 × (32)5 = 311
هیزجت
5
5−6 = ( )
1 6
3
− −4 2 3 −5
3 4 × 32 ÷ 27 = 3 × 3 ÷ 3 = 3 = ( )
1 5
20−6
52 × 4−6
−6
5
= 5 = −8 1 52 5 = ( )
8
4 × 3
7 −6
7 2
4 × 4 4
9
3 × 4 3 × 3 3
3 −2 3 6 9
4
3
= = = ( )
9
3
−2
)مراهچ لصف(
هشیر و ناوت
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.تسا کی ددع لصاح دشاب رفص ناوت هب )رفص زا ریغ( ددع ره : هتکن
؟دیروآ تسد هب ار لباقم ترابع لصاح : لاثم
.میسیون یم 01 ددع زا یناوت تروص هب ار اه نآ کچوک یلیخ دادعا و گرزب یلیخ دادعا رت هداس هبساحم یارب : یملع دامن
.تسا یحیحص ددع? و 2 ≤ ? < 20 نآ رد هک تسا ? × 20? تروص هب تبثم یراشعا ددع ره یملع دامن یلک روط هب : هتکن
زا یناوت زیمم زا دعب یاه مقر دادعت هب سپس هدرک ادج پچ تمس زا مقر کی ادتبا : )تبثم ناوت( گرزب یلیخ دادعا یملع دامن )فلا
.میسیون یم 01 ددع
: دننام
: دننام
)دوش یمن یفنم تقو چیه مه لثم ددع ود روذجم نوچ( .دنرادن )مود هشیر( رذج یفنم دادعا : هتکن
.تسا موس هشیر کی یاراد ددع ره : دادعا موس هشیر )ب
.میهد یم ناشن √3 ? تروص هب ار نآ موس هشیر دشاب یقیقح ددع کی ? رگا : هتکن
: دننام
.دیروآ تسد هب ار ریز یاه رذج لصاح : لاثم
−2
32 + 50 − 2 = 9 + 1 − =
4 4 4
= = 9
1 40 − 1 39 3
4
10
مقر 8
341000000 = 3/41 × 108
مقر 4
14752/93 = 1/475293 × 104
زا لبق یاه مقر دادعت هب سپس هدرک ادج پچ تمس زا رفص فلاخم مقر کی ادتبا : )یفنم ناوت( کچوک یلیخ دادعا یملع دامن )ب
.میسیون یم 01 ددع زا یناوت زیمم
مقر 6
0/0000037 = 3/7 × 10−6 0/00678 = 6/78 × 10−3
.دیسیونب یملع دامن تروص هب ار ریز ترابع لصاح : لاثم
530000 × 0/00027 = 5/3 × 105 × 2/7 × −4 = 14/32 × 101 = 1/432 × 102
10
)یفنم یرگید و تبثم یکی( : تسا مود هشیر ود یاراد ددع ره : دادعا مود هشیر )فلا : یریگ هشیر
42 = (−4)2 = 16 ⇒ √16 = 4 و − 4
)-4 و 4 اب تسا ربارب 06 مود یاه هشیر( : دننام
33 = 27 ⇒ √3 27 = 3
و (−3)3 = −27 ⇒ √3 −27 = −3
√64 × 1 = 8 × 1 = 8
9 3 3
4√3 −125 = 4 × −5 = −20
3
√64 × √−64 = 8 × −4 = −32
√3 0/001 × √√16 = 0/1 × 2 = 0/2
هشیر ای هجرف
)مراهچ لصف(
هشیر و ناوت
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.مینک میسقت مه رب ای برض مه رد ار اه نآ میناوت یم دنشاب ناسکی )هجرف( هشیر یاراد لاکیدار ود رگا : اه لاکیدار میسقت و برض
.مینک یم میسقت ای برض ار اه لاکیدار سپس هدرک میسقت ای برض ار حیحص دادعا ادتبا دنشاب حیحص ددع یاراد اه لاکیدار رگا : هتکن
؟دیروآ تسد هب ار ریز یاه میسقت و برض لصاح : لاثم
نآ زا یکی هک میسیونب یبرض کی ددع یارب هک تروص نیا هب .درک هداس ناوت یم ار اه لاکیدار زا یضعب : اه لاکیدار ندرک هداس
.دشاب هتشاد موس هشیر ای مود هشیر دادعا
: دننام
اب یربج یاه ترابع دننامه ار اه نآ میناوت یم دنشاب مه لثم ندرک هداس زا سپ اه لاکیدار تمسق رگا : اه لاکیدار قیرفت و عمج
.مینک قیرفت ای عمج مه
: دننام
.دینک هداس ار ریز یاه ترابع : لاثم
: دننام
هب لاکیدار ریز ددع هک توافت نیا اب هدرک برض جرخم لاکیدار نامه رد ار جرخم و تروص : دشاب موس هشیر یاراد رسک جرخم )ب
.دوش صخشم لاکیدار ریز ددع ناوت ات هدرک مک ناوت ار هجرف راک نیا یارب .دسرب 3 ناوت
2√2 × √8 = 2√16 = 2 × 4 = 8
8√50 ÷ 4√2 = 2√25 = 2 × 5 = 10
√3 −2 × √3 32 = √3 −64 = −4
9√3 54 ÷ 3√3 2 = 3√3 27 = 3 × 3 = 9
√20 = √4 × 5 = 2√5
مود هشیر
√3 128 = √3 2 × 64 = 4√3 2
موس هشیر
√3 81 = √3 3 × 27 = 3√3 3
موس هشیر
5√2 − 6√5 + 3√2 − 6√2 − 3√5 = 2√2 − 9√5
−5√3 −18√2
2√2 − √75 − 3√72 + 4√3 = 2√2 − √3 × 25 − 3√2 × 36 + 4√3 = −16√2 − √3
3√2 −9√3 2 +2√3 2 −4√2
√18 + 3√3 −54 + √3 16 − 2√8 = √2 × 9 + 3√3 2 × −27 + √3 2 × 8 − 2√2 × 4 = −√2 − 7√3 2
هک میروایب نوریب یلاکیدار تلاح زا ار رسک جرخم تسا مزلا ندرک هداس یارب تاقوا یهاگ : یلاکیدار یاهرسک جرخم ندرک ایوگ
.دوش جراخ یلاکیدار تلاح زا جرخم ات مینک یم برض یددع رد ار جرخم و تروص راک نیا یارب
.مینک یم برض جرخم لاکیدار نامه رد ار جرخم و تروص : دشاب مود هشیر یاراد رسک جرخم )فلا
: دننام
√5 √5 × √5
3 = 3 × √5 = 3√5
5 3√2 3√2 × √2
2 = 2 × √2 = 2 √2 = √2
√
7
3 3
√3 3
√7 √7 × √72
3
= = =
3 3
7
3
√3 3 × √3 72 √3 147 1 1 × √3 ?
√?2 √?2 × √?
= =
3 3
√3 ?
?
3 − 2 = 1
1
6 3
3
)مراهچ لصف(
هشیر و ناوت
t$m çdtş9 uştm ¿t tqLstt
3 − 1w=w2w.riazisara.ir

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.تسا هدش لیکشت )یسیلگنا فورح( ریغتم و دادعا زا هک تسا یترابع : یربج ترابع
)تسا برض( .دشابن یتملاع اه نآ نیب و )ددع و ریغتم( تسا هدش لیکشت تمسق ود زا هک یربج ترابع : یا هلمج کی
: دننام
−1?? ,
?
6
.تسا یباسح ددع ? و ریغتم ? و یقیقح ددع ? هک تسا ??? تروص هب یا هلمج کی یلک مرف : هتکن
.تسا رفص نآ ریغتم نوچ .تسا یا هلمج کی ییاهنت هب یقیقح ددع ره : هتکن
.تسین یا هلمج کی ترابع نآ .دنشاب هتشاد یفنم ناوت فورح ای جرخم رد فورح ای لاکیدار ریز فورح یترابعردرگا : هتکن
.تسا یا هلمج کی ترابع مادک : لاثم
.دنیوگ یم یا هلمج کی نآ هجرد ار ریغتم ناوت : یا هلمج کی هجرد
.دینک لماک ار ریز لودج : لاثم
.دینک هداس ار لباقم یربج ترابع : لاثم
−5?? + ? − 6 + 3?? + 2? − 8? = −2?? − 5? − 6
مه رب اهریغتم و مه رب بیارض میسقت رد و دوش یم برض مه رد اهریغتم و مه رد بیارض برض رد : یا هلمج کی میسقت و برض
.دنوش یم میسقت
.دینک هداس ار ریز یربج یاه ترابع : لاثم
√3??
2
, 4? + 2 ,
−2
, ?? ,
3 2
دراد هلمج ود
7√?
.دنشاب مه لثم لاماک ریغتم ره ناوت و ریغتم هک یا هلمج کی : هباشتم یا هلمج کی
.دنتسه هباشتم ان (−5?2? , 3??2) یلو دنا هباشتم (4?? , −3??) : دننام
.میسیون یم اه نآ رانک ار اهریغتم و مینک یم قیرفت و عمج مه اب ار یا هلمج کی بیارض : هباشتم یاه یا هلمج کی قیرفت و عمج
3?(−4?? − ?) = −12?2? − 3??
24?2?3?
3???
= 8??2
)مجنپ لصف(
یربج یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

مهن لاس
نادهازکیهیحان
یدیلک تاکن و همانسرد
یراکریزدوعسم
.دینک هداس ار ریز یربج یاه ترابع : لاثم
−6?2 + 5?(? − 2?) + 8?? = −6?2 + 5?2 − 10?? + 8?? = −?2 − 2??
.میریگ یم رظن رد ار ریغتم نآ هب تبسن هجرد نیرتگرزب : یا هلمج دنچ هجرد
.تسا 3 ربارب ? هجرد ؟تسا دنچ √5?2?3? − 3?? + 2?3?2 − ? یا هلمج دنچ رد ? ریغتم هب تبسن هجرد : لاثم
.دینک بترم )کچوک هب گرزب زا( ? یلوزن یاه ناوت هب تبسن ار ریز یا هلمج دنچ : لاثم
?2? − 3 + 2?3?2 − 5?? = 2?3?2 + ?2? − 5?? − 3
هب دشاب هتشاد یناسکی رادقم اهریغتم یارب هاوخلد ریداقم مامت یازا اب هک دنشاب یا هنوگ هب یربج ترابع ود رگا : یربج داحتا
.دنیوگ یم داحتا اه نآ یربج یواست
دش یکی یواست فرط ود رگا مینک یم ناحتما هاوخلد ریداقم یازا هب ؟ارچ؟تسا داحتا کی (? − 2)2 = ?2 − 4? + 4 ایآ : لاثم
.تسا داحتا کی یواست نیا
{
? = −4 ⟹ (−4 − 2)2 = (−4)2 − 4(−4) + 4 ⟹ 36 = 36
? = 5 ⟹ (5 − 2)2 = 52 − 4(5) + 4 ⟹ 9 = 9
: یربج )فلا : یا هلمج ود عبرم داحتا
(? + ?)2 = ?2 + 2?? + ?2
{(? − ?)2 = ?2 − 2?? + ?2
2 2 2
(لوا هلمج + مود هلمج) = (لوا هلمج) + مود رد لوا هلمج ربارب ود + (مود هلمج) : یملاک )ب
.دیروآ تسد هب داحتا کمک هب ار ریز یربج یاه ترابع لصاح : لاثم
: یربج )فلا : جودزم داحتا
(? − 2?)2 = ?2 − 2(?)(2?) + (2?)2 = ?2 − 4?? + 4?2
(?? + 3)2 = ?2?2 + 2(??)(3) + 32 = ?2?2 + 6?? + 9
(? + ?)(? − ?) = ?2 − ?2
2 2
(لوا هلمج + مود هلمج) (لوا هلمج − مود هلمج) = (لوا هلمج) − (مود هلمج) : یملاک )ب
.دیروآ تسد هب داحتا کمک هب ار ریز یربج یاه ترابع لصاح : لاثم
(? − 3?)(? + 3?) = ?2 − (3?)2 = ?2 − 9?2
2
? ?
2
(
)2
?
2
2
2
(2? + ) (2? − ) = 2? − ( ) = 4? −
?2
4
)مجنپ لصف(
یربج یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
: کرتشم هلمج داحتا
(? + ?)(? + ?) = ?2 + (? + ?)? + ??
.دیروآ تسد هب داحتا کمک هب ار ریز یربج ترابع لصاح : لاثم
(2? − 3)(2? + 4) = (2?)2 + (−3 + 4)(2?) + (−3 × 4) = 4?2 + 2? − 12
.دنیوگ یم هیزجت ار رگید ترابع دنچ برض لصاح تروص هب یربج ترابع کی نتشون : یربج ترابع هیزجت
اهداحتا زا هدافتسا اب )ب یریگ روتکاف )فلا : هیزجت یاه شور
: میهد یم ماجنا ار ریز لحارم یریگ روتکاف یارب : یریگ روتکاف
مینک یم باختنا ار رتمک ناوت اب کرتشم فورح )3 مینک یم نییعت ار بیارض )م.م.ب( )0 میریگ یم روتکاف ناونع هب ار کرتشم فورح و )م.م.ب( )3
میسیون یم زتنارپ لخاد ار باوج و هدرک میسقت روتکاف لماع رب ار تلامج مامت )4
.دینک هیزجت ار ریز یربج یاه ترابع : لاثم
18?? − 12? = 6?(3? − 2)
دنشاب هتشاد قیقد رذج موس هلمج و لوا هلمج )3
?2 − 6? + 9 = (? − 3)2
دشاب هلمج 3 تلامج دادعت )0 : کرتشم هلمج داحتا کمک هب هیزجت
دنشاب هتشادن قیقد رذج موس هلمج و لوا هلمج )3
دهد یم ناشن ار ددع ود برض لصاح رخآ ددع و عمج لصاح ? بیرض )3
.دینک هداس ار ریز یربج یاه ترابع : لاثم
?2 − 5? + 6 = (? − 3)(? − 2)
دشاب هلمج 3 تلامج دادعت )0 : جودزم داحتا کمک هب هیزجت
دنشاب هتشاد قیقد رذج مود و لوا تلامج )3
دشاب یفنم تملاع تلامج نیب )3
رذج
?
3
16?2? + 4??2 − 8?? = 4??(4? + ? − 2)
دشاب هلمج 3 تلامج دادعت )0 : عبرم داحتا کمک هب هیزجت
2? ?2.دینک هیزجت ار ریز یربج یاه ترابع : لاثم
4?2 + 4??2 + ?4 = (2? + ?2)2
ددع ود عمج ددع ود برض
ددع ود عمج
ددع ود برض
?2 −1? − 12 = (? − 4)(? + 3)
دادعا )م.م.ب(
کرتشم فورح
)مجنپ لصف(
یربج یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

مهن لاس
نادهازکیهیحان
یدیلک تاکن و همانسرد
یراکریزدوعسم
.دینک هداس ار ریز یربج یاه ترابع : لاثم
?1 − 23 = (?1 − 1)(?1 + 1)
هعومجم هلداعمان یاه باوج ی همه .تسا رارقرب یواسمان اه نآ یازا هب هک دنتسهریغتم زا یریداقم هلداعمان یاه باوج : هلداعمان
.دوش یم هتفگ نآ باوج
: دوش یمن ضوع یرباربان تهج دوش مک یددع ای هفاضا ددع یواسم ان کی نیفرط هب رگا : هتکن
? < ? ⟹ ? + ? < ? + ? , ? < ? ⟹ ? − ? < ? − ?
: دوش یمن ضوع یرباربان تهج مینک میسقت تبثم ددع رب ای برض تبثم ددع رد یواسم ان کی نیفرط رگا : هتکن
?
: دوش یم ضوع یرباربان تهج مینک میسقت یفنم ددع رب ای برض یفنم ددع رد یواسم ان کی نیفرط رگا : هتکن
?
? < ? ⟹ ?? > ?? , ? < ? ⟹ ? > ?
?
رذج
?1 − 9 = (? − 6)(? + 6)
3
?2
4
? > 1
? > ? ⟹ ?? > ?? , ? > ? ⟹ ? > ?
? > 1?
? < 1 ? < 1 ?
?
?
2 2
?
2
?2 + < (? − 1)2 ⟹ ?2 + < ?2 − 2? + 1 ⟹ + 2? < 1 ⟹ ? + 4? < 2 ⟹ 5? < 2 ⟹ ? <
2
5
2
باوج هعومجم B = {? ∈ ? ? < }
5
−3
2
5
هلداعمان تهج دشاب یفنم ددع لوهجم بیرض هلداعمان رخا رد رگا هک توافت نیا اب دوش یم لح هلداعم کی دننامه : هلداعمان لح
.دوش یم ضوع
.دیهد شیامن دادعا روحم یور ار اه نآ و هدروآ تسد هب ار ریز یاه هلداعمان باوج هعومجم : لاثم
4(? − 1) ≤ 5? − 2 ⟹ 4? − 4 ≤ 5? − 2 ⟹ 4? − 5? ≤ 4 − 2 ⟹ −? ≤ 2 ⟹ ? ≥ −2
باوج هعومجم A = {? ∈ ? ? ≥ −2}
−3
برض 3 رد نیفرط
.مینک یم هدافتسا ≥ تملاع زا لقادح هملک یاج هب و ≤ تملاع زا رثکادح هملک یاج هب یرباربان هب طوبرم لیاسم رد : هتکن
" .تسا -9 رثکادح رگید ددع ربارب هس هنیرق اب یددع ربارب ود عومجم " : دیسیونب یملاک تروص هب ار ریز ترابع : لاثم
2? + (−3?) ≤ −9
)مجنپ لصف(
یربج یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.دراد دوجو طخ کی هدنهد لیکشت طاقن نیب هک تسا یا هطبار : طخ هلداعم
.دشاب یم (? = ?? + ?) تروص هب طخ هلداعم یلک مرف : هتکن
.دنراد یطخ هطبار مه اب رادقم ود نآ .دشاب تسار طخ تروص هب رادقم ود نیب ی هطبار رادومن هک یتروص رد : هتکن
طیحم شیازفا اب عبرم علض کی شیازفا نوچ .هلب ؟ارچ ؟تسا یطخ ی هطبار عبرم طیحم و عبرم علض کی نیب هطبار ایآ : لاثم
)? = 4? : تشاد میهاوخ سپ میریگ یم رظن رد ? ار عبرم طیحم و ? ار عبرم علض( : تسا تباث رادقم کی عبرم
?
? = 4?
تحاسم شیازفا اب عبرم علض کی شیازفا نوچ .ریخ ؟ارچ ؟تسا یطخ ی هطبار عبرم تحاسم و عبرم علض کی نیب هطبار ایآ : لاثم
)? = ?2 : تشاد میهاوخ نیربانب میریگ یم رظن رد ? ار عبرم تحاسم و ? ار عبرم علض( : تسین یتباث رادقم عبرم
?
? = ?2
(? = ?? + ? ∶ یلک مرف) رذگ ادبم ریغ )3 (? = ?? ∶ یلک مرف) رذگ ادبم )0 : طخ هلداعم عاونا
(? = ? , ? = ? ∶ یلک مرف) روحم اب یزاوم طوطخ )3
.تسا هطقن ود تاصتخم هب زاین تاصتخم هاگتسد رد طخ کی مسر یارب : طخ کی مسر
میهد یم رارق )0 و رفص ( دادعا ? یاج هب لودج رد دشاب حیحص ددع ? زا لبق ددع طخ هلداعم )درادناتسا( یلک مرف رد رگا : هتکن
.میهد یم رارق )رسک جرخم و رفص ( دادعا ? یاج هب دشاب یرسک ددع ? زا لبق ددع و
.دینک مسر تاصتخم هاگتسد رد ار ? = 3? طخ هلداعم : لاثم
?
? = 3?
0
1
0
3
رذگ ادبم طخ
)مشش لصف(
یطخ یاه هلداعم و طخ
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
2
3
.دینک مسر تاصتخم هاگتسد رد ار ? = − ? + 4 طخ هلداعم : لاثم
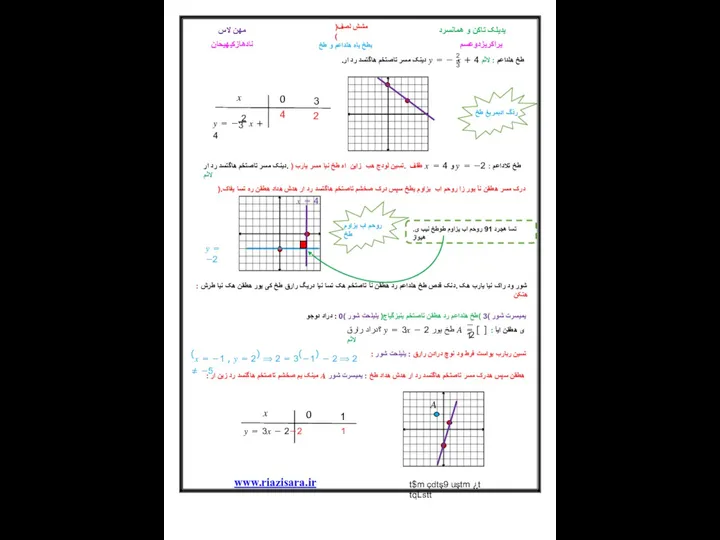
شور ود راک نیا یارب هک .دنک قدص طخ هلداعم رد هطقن نآ تاصتخم هک تسا نیا دریگ رارق طخ کی یور هطقن هک نیا طرش : هتکن
یمیسرت شور )3 )طخ هلداعم رد هطقن تاصتخم ینیزگیاج( یلیلحت شور )0 : دراد دوجو
−1
2
؟دراد رارق ? = 3? − 2 طخ یور ? = [ ] ی هطقن ایآ : لاثم
: تسین ربارب یواست فرط ود نوچ درادن رارق : یلیلحت شور
?
3
? = − 2 ? + 4
0
3
4
2
رذگ ادبمریغ طخ
? = −2
طقف .تسین لودج هب زاین اه طخ نیا مسر یارب ( .دینک مسر تاصتخم هاگتسد رد ار ? = 4 و ? = −2 طخ تلاداعم : لاثم
).درک مسر هطقن نآ یور زا روحم اب یزاوم یطخ سپس درک صخشم تاصتخم هاگتسد رد ار هدش هداد هطقن ره تسا یفاک
? = 4
روحم اب یزاوم طخ
.تسا هجرد 91 روحم اب یزاوم طوطخ نیب ی هیواز
(? = −1 , ? = 2) ⟹ 2 = 3(−1) − 2 ⟹ 2 ≠ −5
?
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt
0
1
? = 3? − 2 −2
1
: مینک یم صخشم تاصتخم هاگتسد رد زین ار ? هطقن سپس هدرک مسر تاصتخم هاگتسد رد ار هدش هداد طخ : یمیسرت شور
?
)مشش لصف(
یطخ یاه هلداعم و طخ

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
? یاج هب راب کی و ? یاج هب راب کی لودج رد .دنتسه (?? + ?? = ?) تروص هب هک یطخ تلاداعم مسر یارب : هتکن
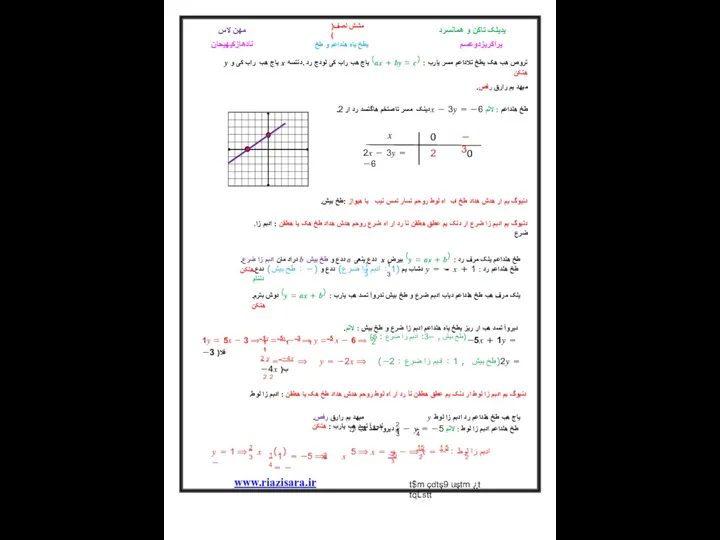
.میهد یم رارق رفص
.دینک مسر تاصتخم هاگتسد رد ار 2? − 3? = −6 طخ هلداعم : لاثم
.دنیوگ یم ار هدش هداد طخ اب اه لوط روحم تسار تمس نیب یا هیواز :طخ بیش
.دنیوگ یم ادبم زا ضرع ار دنک یم عطق هطقن نآ رد ار اه ضرع روحم هدش هداد طخ هک یا هطقن : ادبم زا ضرع
.دراد مان ادبم زا ضرع ? ددع و طخ بیش ? ددع ینعی ? بیرض (? = ?? + ?) طخ هلداعم یلک مرف رد : هتکن
1 1
3 3
.دشاب یم (1 ∶ ادبم زا ضرع) ددع و (− ∶ طخ بیش) ددع ? = − ? + 1 طخ هلداعم رد : دننام
.دوش بترم (? = ?? + ?) یلک مرف هب طخ هلداعم دیاب ادبم ضرع و طخ بیش ندروآ تسد هب یارب : هتکن
.دیروآ تسد هب ار ریز یطخ یاه هلداعم ادبم زا ضرع و طخ بیش : لاثم
1 1 1 1
2 ? = −4? ⟹ ? = −2? ⟹ (−2 ∶ طخ بیش , 1 ∶ ادبم زا ضرع) 2? = −4? )ب
2 2
.دنیوگ یم ادبم زا لوط ار دنک یم عطق هطقن نآ رد ار اه لوط روحم هدش هداد طخ هک یا هطقن : ادبم زا لوط
.میهد یم رارق رفص ? یاج هب طخ هلداعم رد ادبم زا لوط ندروآ تسد هب یارب : هتکن
3
2 1
4
.دیروآ تسد هب ار ? − ? = −5 طخ هلداعم ادبم زا لوط : لاثم
2
3
? = 1 ⟹ ? −
1 4
2
3
(1) = −5 ⟹ ? = −
−5
2
3
2
15 1 5
2
5 ⟹ ? = = − ⟹ ? = − ∶ ادبم زا لوط
?
2? − 3? = −6
0
−3
2
0
2
1? = 5? − 3 ⟹ 1? = 5? − 3 ⟹ ? = 5 ? − 6 ⟹ (5 : طخ بیش , −3: ادبم زا ضرع)−5? + 1? = −3 )فلا
)مشش لصف(
یطخ یاه هلداعم و طخ
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
(? = −6? , ? = −6? + 5) : دننام .دنشاب ربارب طخ ود بیش هک دنتسه یزاوم یتروص رد طخ ود : هتکن
طخ بیش ود برض لصاح ای دنشاب رگیدکی سوکعم و هنیرق طخ ود بیش هک دنتسه دومع مه رب یتروص رد طخ ود : هتکن
1
(? = 1? + 6 , ? = − 2 ? − 1) : دننام .دوش −1 ددع اب ربارب
1
بترم ار طخ هلداعم ادتبا .درذگب ? = [−2] ی هطقن زا و یزاوم ? − 3? = 5 طخ اب هک دیسیونب یطخ هلداعم : لاثم
: دوش صخشم طخ بیش ات هدرک
−3? = −? + 5 ⟹ −3? = − ? + 5 ⟹ ? = 1 ? − 5 ⟹ ? = 1
−3 −3 −3 3 3 3
(?= 2 ,?=−1)
6
? = ?? + ? ⇒ 6 ? = 2 ? − 1
1
5
−1
2
صخشم طخ بیش .درذگب ? = [ ] ی هطقن زا و دشاب دومع ? = − ? + 2 طخ اب هک دیسیونب یطخ هلداعم : لاثم
: میروآ تسد هب ار ادبم زا ضرع دیاب سپ تسا
(?=5 ,?=−2 ,?=1)
? = ?? + ? ⇒ 1 = 5(−
2) + ? ⟹ ? = 7
(?=5 ,?=7)
? = ?? + ? ⇒ ? = 5? + 7
: مینک یم هدافتسا ریز ی هطبار زا درذگ یم هطقن ود زا هک یطخ بیش ندروآ تسد هب یارب : هتکن
? = اه ضرع لضافت = ?2−?1
اه لوط لضافت ?2−?1
2
−1
4 3
.درذگب ? = [ ] و ? = [ ] طاقن زا هک دیسیونب یطخ هلداعم : لاثم
? = 1−6 = − 2
−2−1 6
(?=− 2 ,?=1 ,?=6)
, ? = ?? + ? ⇒ 6 6 = − 2 (1) + ? ⟹ ? = 22
6 6
6 6
(?=− 2 ,?=22)
2
6
? = ?? + ? ⇒ ? = − ? +
22
6
موس و لوا عبر زاسمین طخ هلداعم و (? = 1) اه ضرع روحم طخ هلداعم و (? = 1) اه لوط روحم طخ هلداعم : هتکن
.دشاب یم (? = −?) مراهچ و مود عبر زاسمین طخ هلداعم و (? = ?)
دیدج طخ هلداعم
ادبم زا ضرع
ربارب طخ ود بیش
سوکعم و هنیرق طخ ود بیش
دیدج طخ هلداعم
دیدج طخ هلداعم
)مشش لصف(
یطخ یاه هلداعم و طخ
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
: درک هدافتسا ناوت یم ریز یاه شور زا یطخ تلاداعم هاگتسد لح یارب : یطخ تلاداعم هاگتسد
.دیآ یم تسد هب مود ریغتم ینیزگیاج اب سپس هدرک فذح ار اهریغتم زا یکی شور نیا رد : یفذح شور )فلا
)یفذح شور( .دینک لح ار ریز یلوهجم ود تلاداعم هاگتسد : لاثم
هلداعم رد ار نآ رادقم و هدرک بترم ریغتم کی بسح رب ار تلاداعم زا یکی شور نیا رد : )یلیدبت( ینیزگیاج شور )ب
.میهد یم رارق مود
)ینیزگیاج شور( .دینک لح ار ریز یلوهجم ود تلاداعم هاگتسد : لاثم
−4? + ? = −7
⟹ { 4? + 6? = 14
−4? + ? = −7
7? = 7 ⟹ ? = 1
2? + 3(1) = 7 ⟹ 2? = 4 ⟹ ? = 2
2
1
? = [ ]
یلوهجم ود هاگتسد باوج
2? + 3? = 7
{−4? + ? = −7
⟹ {
3 7
2
3 7
2
−4 (− ? + ) + ? = −7 ⟹ 6? − 14 + ? = −7 ⟹ 7? = 7 ⟹ ? = 1
2 { 2? + 3? = 7
)مینک یم بترم ? بسح رب2( ? = −3? + 7 ⟹ ? = − ? +
2 2
)میهد یم رارق ینییاپ هلداعم رد ار ? رادقم(
? = − 3 (1) + 7 ⟹ ? = − 3 + 7 = 4 = 2 ⟹ ? = 2 2 2 2 2 2
یلوهجم ود هاگتسد باوج
1
? = [2]
.درک لح ار نآ یاه شور زا یکی هب و درک هدافتسا یلوهجم ود هاگتسد زا ناوت یم لیاسم زا یضعب لح یارب : هتکن
)ینیزگیاج شور( .دیروآ تسد هب ار کی ره نس .تسا لاس 08 اه نآ نس فلاتخا و .تسا وا نس ربارب 3 یلع ردارب نس : لاثم
).مینک یم ضرف ? ار یلع نس و ? ار یلع ردارب نس (
{
? = 3?
⟹ {
? = 3?
? − ? = 18 3? − ? = 18 ⟹ 2? = 18 ⟹ ? = 9
? = 3(9) = 27 ⟹ ? = 27
یلع نس
یلع ردارب نس
)مشش لصف(
یطخ یاه هلداعم و طخ
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.دنشاب یا هلمج دنچ نآ جرخم و تروص هک تسا یرسک : ایوگ ترابع
: دننام
.تسین ایوگ .دشاب ناوت رد ای رسک جرخم رد ای قلطم ردق لخاد ای لاکیدار ریز ای یفنم ناوت نآ ریغتم هک یترابع : هتکن
: دننام
.تسا هدشن فیرعت دنک یم رفص ار رسک جرخم هک یریداقم یازا هب ایوگ ترابع : هتکن
.تسا هدشن فیرعت رسک جرخم زا یریداقم هچ یازا هب ریز ایوگ یاه ترابع : لاثم
سپس هتشون یربج ترابع دنچ ای ود برض لصاح تروص هب ار جرخم و تروص ندرک هداس یارب : ایوگ ترابع ندرک هداس
.مینک یم هداس جرخم و تروص زا ار یواسم یاه ترابع
.مینک یم هدافتسا داحتا و یریگروتکاف زا ایوگ یاه ترابع ندرک هداس یارب : هتکن
.دینک هداس ار ریز ایوگ یاه ترابع : لاثم
.مینک یم برض جرخم رد جرخم و تروص رد تروص سپس مینک یم هداس ادتبا ایوگ یاه ترابع برض رد : ایوگ یاه ترابع برض
.مینک یم برض یمود رسک سوکعم رد ار یلوا رسک ینعی مینک یم لیدبت برض هب ار میسقت ادتبا : ایوگ یاه ترابع میسقت
, ,
4?2 − 1 √5? ? − 3
2? + 3 2 ?
|? − 2| ,
?
,
? 4 − √?
3 3?
?2 − 5
2? − 4
)دنوش صخشم هدشن فیرعت ریداقم ات هداد رارق رفص یواسم ار رسک جرخم(
⟹ 2? − 4 = 1 ⟹ 2? = 4 ⟹ ? = 2 )تسا هدشن فیرعت (? = 2) یازا هب ایوگ ترابع (
? − 4
?2 − 4?
? = 1
⟹ ?2 − 4? = 1 ⟹ ?(? − 4) = 1 ⟹ {? − 4 = 1 ⟹ ? = 4
)تسا هدشن فیرعت (? = 4 , ? = 1) یازا هب ایوگ ترابع (
=
(? − 2)(? + 2)
?(? + 2)
=
(? − 2)
?
?2 − 5? + 6 = ( ? − 3)(? − 2) = (? − 2)
جودزم داحتا
?2 − 4
?2 + 2?
یریگروتکاف
کرتشم هلمج داحتا
?2 − 6? + 9 (? − 3)(? − 3) (? − 3)
یا هلمج ود عبرم داحتا
یریگروتکاف
)متفه لصف(
ایوگ یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
ترابع لصاح رخآ رد و هداد باوج هناگادج ار رسک جرخم ترابع و رسک تروص ترابع : بکرم یاه ترابع ندرک هداس
.مینک یم میسقت جرخم ترابع لصاحرب ار تروص
.دیسیونب تروص نیرت هداس هب ار ریز ترابع لصاح : لاثم
.دیروآ تسد هب ار ریز ایوگ یاه ترابع میسقت و برض لصاح : لاثم
? + 5 × ? + 2 = (? + 5) × (? + 2) = 1 3? + 6 ?2 − 25 3(? + 2) (? − 5)(? + 5) 3(? − 5)
?2 − 2? − 15 ÷ ?2 − ? − 12 = ( ? − 5)(? + 3) × 2(? + 3) = 2 (? + 5)
? + 3 2? + 6 (? + 3) (? − 4)(? + 3) (? − 4)
.مینک یم باختنا ار اه جرخم )م.م.ک( کرتشم جرخم اه جرخم نیب : ایوگ یاه ترابع قیرفت و عمج
.دیروآ تسد هب ار ریز یاه قیرفت و عمج لصاح : لاثم
2? + 3 + ? − 4 = (2? + 3)(? − 2) + (? − 4)(? + 1) = 3?2 − 4? − 11
? − 3 ?2 − 9 (? − 3)(? + 3)
? + 1 ? − 2 (? + 1)(? − 2) (? + 1)(? − 2)
? − 1 − ? + 5 = ( ? − 1)(? + 3) − (? + 5) =
?2 + ? − 8
(? − 3)(? + 3)
3 4
?2
1 − 6 − 1
?
?2 − ? + 1 =
3 − 4? + ?2
?2
?2 − 6 − ?
?2
?2
(? − 3)(? − 1)
= ×
?2
(? − 1)
=
(? − 3)(? + 2) (? + 2)
?3 ?3 ?4
اب )اهریغتم( فورح )3 دنوش یم هداس مه اب دادعا )3 هدش برض مه رد اه تملاع )0 : یا هلمج کی رب یا هلمج کی میسقت
)دوش یم هدافتسا راد ناوت دادعا میسقت هدعاق زا اهریغتم ندرک هداس رد( : دنوش یم هداس مه
.دینک هداس ار ریز ایوگ ترابع : لاثم
−18?5?2?4 = −18 × ?5 × ?2 × ?4 = − 3?2
12?3?3?4 12 2?
)متفه لصف(
ایوگ یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
.مینک یم میسقت رسک جرخم رب ار رسک تروص تلامج کت کت : یا هلمج کی رب یا هلمج دنچ میسقت
.دینک هداس ار ریز ایوگ ترابع : لاثم
: میهد یم ماجنا بیترت هب ار ریز لحارم میسقت نیا یارب : یا هلمج دنچ رب یا هلمج دنچ میسقت
.میسیون یم ناوت نیرتمک هب ناوت نیرتشیب زا ینعی درادناتسا لکش هب ار هیلع موسقم و موسقم ادتبا )0
.میسیون یم تمسق جراخ رد ار لصاح و هدرک میسقت هیلع موسقم ی هلمج نیلوا رب ار موسقم ی هلمج نیلوا )3
.مینک یم مک مه زا ار ترابع ود و هتشون موسقم ترابع ریز ار لصاح و هدرک برض هیلع موسقم تلامج کت کت رد ار تمسق جراخ )3 زا هدنام یقاب هجرد هک میهد یم همادا ییاج ات ار رارکت نیا و مینک رارکت ار 3 و 3 لحارم هدمآ تسد هب یا هلمج دنچ یارب )4
.دوش رتمک هیلع موسقم هجرد
.دیروآ تسد هب ار ریز
: میسقت هطبار
: دوش رفص میسقت هدنام یقاب ینعی ندوب ریذپشخب
4?5 − 6?3 + 12? 4?5 6?3
12?
2? 2? 2? 2?
= − + = 2?4 − 3?2 + 6
?2
?
=: )?هیلع موسقم رب موسقم میسقت( مود هلحرم
?(? − 2) = ?2 −:2)ه?یلع موسقم رد تمسق جراخ برض لصاح( موس هلحرم
4? − ?2 + 7 + 2?2 ÷ ? −می2سقت هدنام یقاب و تمسق جراخ : لاثم
4? − ?2 + 7 + 2?2 = ?2 + 4? +: )7ترابع ندرک درادناتسا( لوا هلحرم
? − 2
?2 + 4? + 7
−(?2 − 2?)
6? + 7
−(6? − 12)
? + 6
تمسق جراخ
هدنام یقاب 19
(? − 2)(? + 6) + 19 = ?2 + 4? + 7
.تسا ریذپشخب هیلع موسقم رب موسقم .دوش رفص هدنام یقاب ترابع ود میسقت رد رگا : هتکن
.دشاب ریذپشخب ?2 − 5 رب ?4 − 3?2 + ? − 3 یا هلمج دنچ هک دیبایب یروط ? رادقم : لاثم
?4 − 3?2 + ? − 3 ?2 − 5
−(?3 − 5?2) ?2 + 2
2?2 + ? − 3
−(2?2 − 11)
? + 7
? + 7 = 1 ⟹ ? = −7
)متفه لصف(
ایوگ یاه ترابع
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
مهن لاس
نادهازکیهیحان
یم ناشن (?) یسیلگنا فرح اب ار مجح و دراد مان )شیاجنگ( مجح دنک یم لاغشا مسج کی هک ار ییاضف رادقم : مجح
.دنهد
یورک مجح )3 یطورخم ای یمره مجح )3 یروشنم مجح )0 : مجح عاونا
طاقن هلصاف نیا هب .دشاب هزادنا کی هب )هریاد زکرم( مان هب هطقن کی زا طاقن مامت هلصاف هک هحفص زا یطاقن هعومجم : هریاد
.دنهد یم ناشن ?(? , ?) تروص هب راصتخا هب ار هریاد : هتکن
هحفص طاقن هلصاف نیا هب .دشاب هزادنا کی هب )هرک زکرم( مان هب هطقن کی زا طاقن مامت هلصاف هک اضف زا یطاقن هعومجم : هرک
.دنیوگ یم )هرک عاعش( هریاد زکرم ات
: هرک مجح لومرف
: هرک تحاسم لومرف
.دیروآ تسد هب ار رتم یتناس 4 رطق اب هرک تحاسم و مجح : لاثم
.تسا هدش طیحم هرک رب هناوتسا و هدش طاحم هناوتسا رب هرک مییوگ یم .دریگ رارق هناوتسا لخاد لماک روط هب هرک رگا : هتکن
هریاد
زکرم
.دنیوگ یم )هریاد عاعش( هریاد زکرم ات هحفص
عاعش
پوت و نیمز هرک : دننام
3
? = 4 ??3
? = 4??2
4 ÷ 2 = 2 هرک عاعش
? = 4 ??3 = 4 × 3/14 × 23 = 33/49 3 3
? = 4??2 = 4 × 3/14 × 22 = 51/24
.تسا دنچ هرک تحاسم هب هرک مجح یددع تبسن : لاثم
?
4 ??3
? 4??2 3
= 3 = 1 ?
)متشه لصف(
تحاسم و مجح
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

یدیلک تاکن و همانسرد
یراکریزدوعسم
: تسا هدش طاحم رتم یتناس 6 رطق هب یا هناوتسا رد یا هرک : لاثم
.دیروآ تسد هب ار هرک مجح )فلا
.دیروآ تسد هب ار هناوتسا مجح )ب
.دیروآ تسد هب ار هناوتسا و هرک نیب یاضف مجح )ج
.دوش یم لصاح هرک رطق لوح هریاد مین نارود زا : هتکن
.دوش یم لصاح هرک مین عاعش لوح هریاد عبر نارود زا : هتکن
3
.درک هدافتسا ? = 2 ??3 ی هطبار زا ناوت یم هرک مین مجح ندروآ تسد هب یارب : هتکن
)? بسح رب( .دیروآ تسد هب ار رتم یتناس 4 عاعش لوح هریاد عبر نارود زا لصاح مجح : لاثم
)دوش یم لصاح هرک مین عاعش لوح هریاد عبر نارود زا(
مهن لاس
نادهازکیهیحان
6 ÷ 2 = 3 ?? هرک عاعش
? = 4 ??3 = 4 × 3/14 × 33 = 113/14 ??3
3 3
? = ? × ℎ = (3 × 3 × 3/14) × 6 = 169/56 ??3
169/56 − 113/14 = 56/52 ??3
? = 2 ??3 = 2 ? × 43 = 42/66 ?
3 3
????هدعاق
.دش دهاوخ ربارب ?6 هرک مجح و ?1 هرک تحاسم مینک ربارب ? ار هرک عاعش رگا : هتکن
.دش دهاوخ ربارب دنچ هرک مجح و تحاسم مینک ربارب 4 ار یا هرک عاعش رگا : لاثم
? = ?2 = 42 = 16 ربارب ? = ?3 = 43 = 64 ربارب
.دشاب بدحم یعلض دنچ نآ )هدعاق( نیریز هجو و ثلثم نآ یبناج حطس هک ییاضف لکش : مره
.دنیوگ یم مره عافترا هدعاق ات مره سار هلصاف هب : هتکن
?مره سار
??مره عافترا
)ثلثم( یبناج حطس
)متشه لصف(
تحاسم و مجح
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt

مهن لاس
نادهازکیهیحان
یدیلک تاکن و همانسرد
یراکریزدوعسم
: یملاک )فلا : مره مجح
: یربج )ب
.دیروآ تسد هب ار رتم یتناس 6 عافترا و رتم یتناس 5 علض هب یا هدعاقلا عبرم مره مجح : لاثم
.تسا
.دنتسه ربارب مجح یاراد .دنشاب ناسکی عافترا و تحاسم مه یاه هدعاق یاراد مره ود رگا : هتکن
: طورخم مجح
: یملاک )فلا
: یربج )ب
.دینک باسح ار ریز طورخم مجح : لاثم
1
3
مره مجح = × هدعاق تحاسم × عافترا
3
? = 1 ?. ℎ
? = 1 ?. ℎ = 1 × (5 × 5) × 6 = 51 ??3
3 3
? =
1 1 6 × 8
3
?. ℎ = × (
3 2
) × 5 = 41 ??3
(عبرم ? = علض کی × شدوخ)
رطق ود برض لصاح
2
(یزول ? = )
عبرم تحاسم
بعکم رتم یتناس دنچ مره مجح دشاب رتم یتناس 5 مره عافترا رگا .تسا رتم یتناس 8 و 6 یاهرطق اب یزول هدعاق : لاثم
یزول تحاسم
طورخم مجح = × هدعاق تحاسم × عافترا
3 3
3
? = 1 ?. ℎ = 1 ??2ℎ
?طورخم سار
هریاد زکرم طورخم عافترا یاپ و هریاد نآ هدعاق هک مظتنم مره یا هیبش یلکش : طورخم
.دشاب
??طورخم دلوم
??طورخم عافترا
??هدعاق عاعش
1
? = 1 ??2ℎ = 1 × 3/14 × 22 × 6 = 25/12 ??3
3 3
?
?
?
)متشه لصف(
تحاسم و مجح
www.riazisara.ir
t$m çdtş9 uştm ¿t tqLstt