Презентация на тему АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

Девиз урока:
« Способность к восприятию математики развита у человека пожалуй также как способность получать удовольствие от приятной музыки, она присуща огромному большинству» / Годфри Харди/

Вопросы для повторения:
1. Определение арифметической прогрессии.
2.Как найти разность арифметической прогрессии, если известны два ее члена a m и аn ,где m>n?
3. Сформулировать характеристическое свойство арифметической прогрессии ( формула).
4. Запишите формулу n-ого члена арифметической прогрессии .
5. Запишите формулу суммы n первых членов арифметической прогрессии (2 способа).

Устные упражнения:
1.Найдите член арифметической прогрессии, обозначенный буквой: 3;6; а3;12…..
А)8; Б)9; В)10; Г)5. /ответ поясните/
2.Найдите члены арифметической прогрессии, обозначенные буквами: а1;-8;а3;-4…..
А)10 и 6; Б)-10 и 6; В)-10 и -6 /ответ поясните/
3.Является ли арифметической прогрессией числовая последовательность: А)аn=n2 +5;
Б)an =5n+4; В) an =(-0,5+4n):2n? /ответ поясните/
4.Какое из чисел не является членом арифметической прогрессии:5;10;15….
А)80; Б)95; В)100; Г)112? /ответ поясните/

БУДЬ ВНИМАТЕЛЕН:
Фигура состоит из столбцов как показано на рисунке.
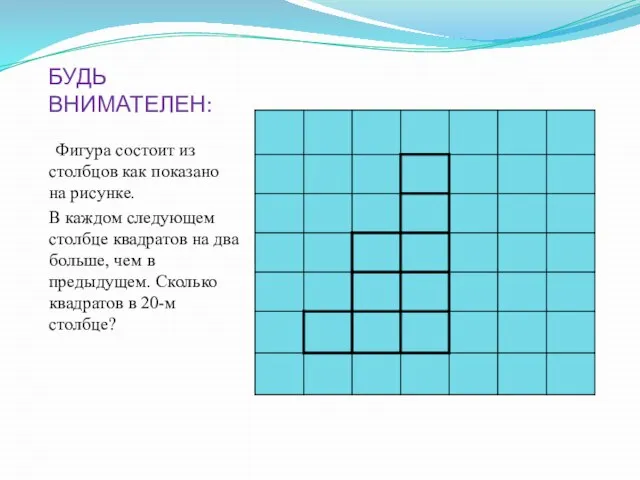
В каждом следующем столбце квадратов на два больше, чем в предыдущем. Сколько квадратов в 20-м столбце?

БУДЬ ВНИМАТЕЛЕН:
Фигура составлена из квадратов, как показано на рисунке.
В каждом следующем ряду квадратов на два больше, чем в предыдущем. Сколько квадратов в 15-м ряду?

ПРАКТИЧЕСКАЯ РАБОТА:

МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ ЗАКЛЮЧАЕТСЯ В СЛЕДУЮЩЕМ:
Утверждение, зависящее от натурального числа n , верно при любом n , если выполняются два условия:
Утверждение справедливо при n =1; /базис индукции/
Из справедливости утверждения при n= k следует его справедливость при n = k +1 / индукционный шаг/.

Конструктивно- вариативный тест
1.Метод, позволяющий доказывать утверждения зависящие от натурального числа n называется методом……………………
2.Первый шаг в доказательстве называется……………………………………………………
3.Если утверждение справедливо при n=……..
4.Второй шаг в доказательстве называется………………………………………………..
5. Из справедливости утверждения при n=k следует его справедливость при n=…………..