Содержание
- 2. Свойства степеней Одинаковые основания Что это? Как это? (a n)m = a n ∙ a m
- 3. Степень чисел, оканчивающихся нулями 2. К результату приписать столько нулей, сколько их в основании, умноженном на
- 4. Степень десятичной дроби 2. Справа налево отсчитать столько знаков, сколько их в произведении количества знаков после
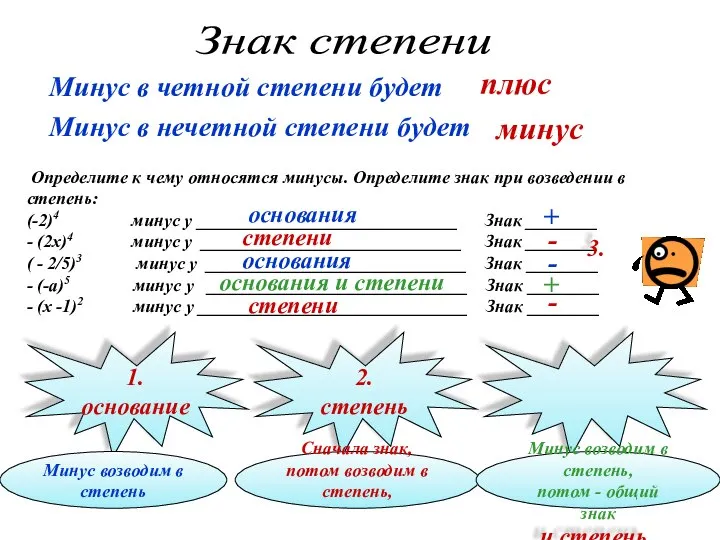
- 5. Знак степени Минус в четной степени будет плюс Минус в нечетной степени будет минус Определите к
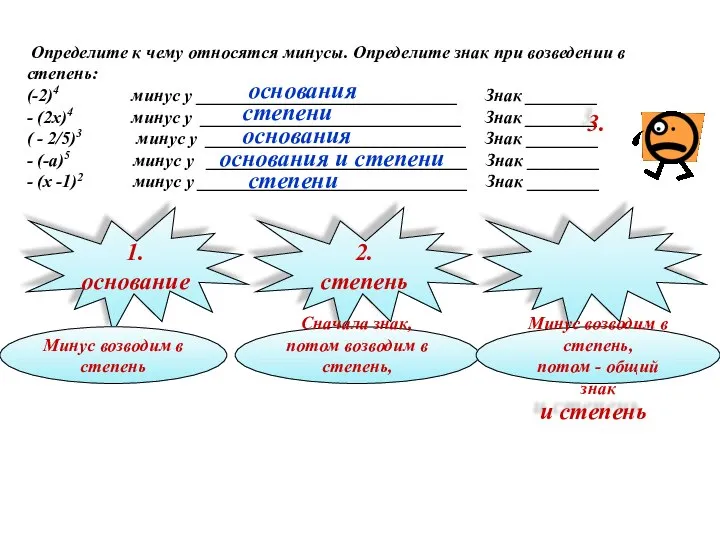
- 6. Определите к чему относятся минусы. Определите знак при возведении в степень: (-2)4 минус у _____________________________ Знак
- 7. Определите к чему относятся минусы. Определите знак при возведении в степень: (-2)4 минус у _____________________________ Знак
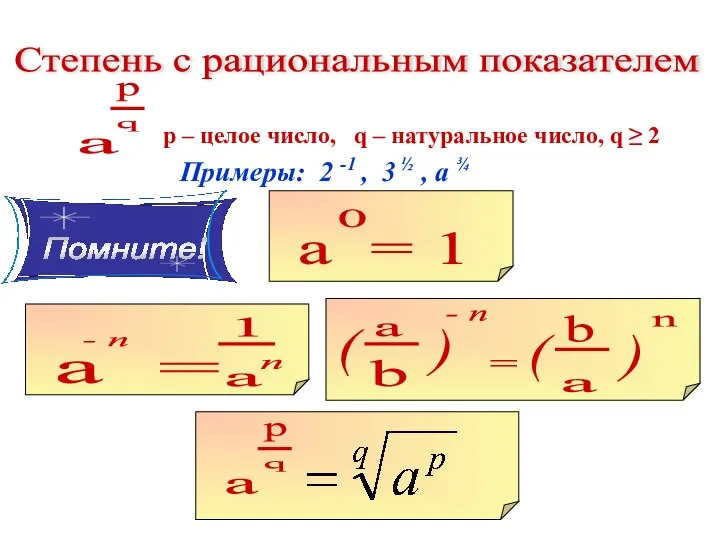
- 8. Степень с рациональным показателем р – целое число, q – натуральное число, q ≥ 2 Примеры:
- 9. Свойства степеней Одинаковые основания Что это? Как это? (a n)m = a n ∙ a m
- 10. Свойства степеней с рациональным показателем такие же как свойства степеней с натуральным показателем а 1/5 ·
- 11. Действия в выражениях, содержащих степени Действия с числовыми основаниями 1. Разложение числа на простые множители. Представьте
- 12. 2. Сокращение дробей 2. Определить знак; (можно определять сначала); 1. Возвести в степень при наличии; выполнить
- 13. При сокращении дробей числовые основания разложить на множители При сокращении буквенной части – сокращать на букву
- 14. 3. Преобразование выражений со степенями 2. Выполнить действия, используя свойства степеней или арифметические действия и таблицу
- 16. Скачать презентацию










 Сложение и вычитание дробей
Сложение и вычитание дробей Евклид – отец геометрии
Евклид – отец геометрии Статистическое изучение связей между явлениями (4 часа). Тема 1.7
Статистическое изучение связей между явлениями (4 часа). Тема 1.7 Олимпийские игры: история, современность и математика
Олимпийские игры: история, современность и математика Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Презентация на тему ЗАДАЧИ НА ЧАСТИ
Презентация на тему ЗАДАЧИ НА ЧАСТИ  Методы расчета КИХ-фильтров
Методы расчета КИХ-фильтров Путь и перемещение
Путь и перемещение Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений Геометрические решения тригонометрических задач
Геометрические решения тригонометрических задач Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Вписанная и описанная призмы. Задания
Вписанная и описанная призмы. Задания Задачи. Длина обхвата дерева и площадь его поперечного сечения
Задачи. Длина обхвата дерева и площадь его поперечного сечения Геометрия Евклида
Геометрия Евклида Присчитывание и отсчитывание по 2
Присчитывание и отсчитывание по 2 Обыкновенные дроби. Задания для устного счета. 8 класс
Обыкновенные дроби. Задания для устного счета. 8 класс Интерактивная игра уроки математики в Школе Смешариков
Интерактивная игра уроки математики в Школе Смешариков Объем пирамиды
Объем пирамиды Л 6 Элементарные функции
Л 6 Элементарные функции Корень степени n
Корень степени n Доказательство равносильностей
Доказательство равносильностей Векторы. Сложение и вычитание векторов
Векторы. Сложение и вычитание векторов Расстояние между двумя точками. Координаты середины отрезка
Расстояние между двумя точками. Координаты середины отрезка Алгоритмы. Повторение
Алгоритмы. Повторение Основные принципы комбинаторики
Основные принципы комбинаторики Великолепная пятерка. Игра
Великолепная пятерка. Игра Результаты пробных ЕГЭ по математике (2013-2014 учебный год)
Результаты пробных ЕГЭ по математике (2013-2014 учебный год)