Содержание
- 2. Модуль «ГЕОМЕТРИЯ» №10 Повторение (2) Ответ: 4. Найти АС. В С А 5 ⇒ ⇒ По
- 3. Повторение Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе В прямоугольном треугольнике квадрат
- 4. Модуль «ГЕОМЕТРИЯ» №10 Повторение (2) Ответ: 17. Найти АВ. В С А 15 ⇒ ⇒ По
- 5. Повторение Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему В прямоугольном треугольнике квадрат
- 6. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 52. Найти АВ. В С А 26 BH=HA, зн. АВ=2
- 7. Повторение Высота в равнобедренном треугольнике, проведенная к основанию, является и медианой В прямоугольном треугольнике сумма острых
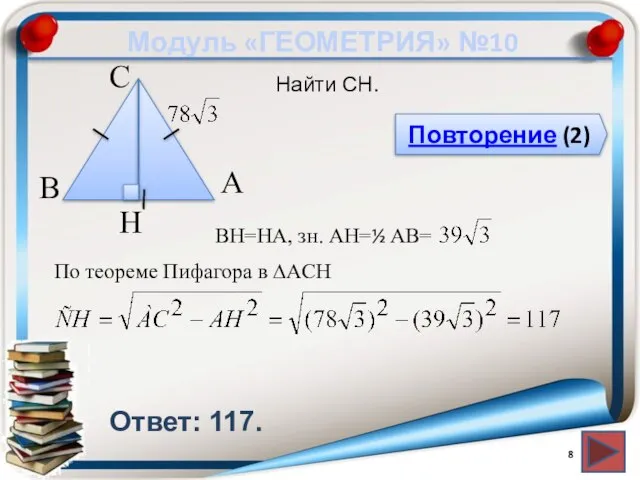
- 8. Модуль «ГЕОМЕТРИЯ» №10 Повторение (2) Ответ: 117. Найти CH. В А H С BH=HA, зн. АH=½
- 9. Повторение Высота в равнобедренном треугольнике, проведенная к основанию, является и медианой В прямоугольном треугольнике квадрат гипотенузы
- 10. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 75. Найти AB. В А H С 120⁰ Проведем высоту
- 11. Повторение Высота в прямоугольном треугольнике, проведенная к основанию является биссектрисой и медианой В прямоугольном треугольнике катет,
- 12. Модуль «ГЕОМЕТРИЯ» №10 Повторение (4) Ответ: 5. Дано: параллелограмм, P=10, АЕ:ЕD=1:3. Найти AD В А D
- 13. Повторение Биссектриса – это луч, который делит угол пополам Периметр многоугольника – это сумма длин всех
- 14. Модуль «ГЕОМЕТРИЯ» №10 Повторение (2) Ответ: 66. АВСD – прямоугольник, ∠1:∠2=1:2. Найти АС. В А D
- 15. Повторение Прямоугольник – это параллелограмм с прямыми углами Катет, лежащий против угла в 30⁰, равен половине
- 16. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 52. АВСD параллелограмм. Найти большую сторону 2 3 4 1
- 17. Повторение Если две параллельные прямые пересечены третьей, то накрест лежащие углы равны Если в треугольнике два
- 18. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 49. АВСD – ромб. Найти меньшую диагональ. В А D
- 19. Повторение Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам Катет прямоугольного треугольника, лежащий
- 20. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 22. В А D С 44 12 М К Е
- 21. Повторение Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции Параллельные прямые, проведенные через
- 22. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 103. АВСD – трапеция, СЕ||АВ. P∆CDЕ =69. Найти P трапеции
- 23. Повторение Если в четырехугольнике противоположные стороны параллельны, то такой четырехугольник - параллелограмм В параллелограмме противоположные стороны
- 24. Модуль «ГЕОМЕТРИЯ» №10 Повторение (2) Ответ: 37. АВСD – трапеция В А D С 29 21
- 25. Повторение Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции Средняя линия трапеции равна
- 26. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 94. АВСD – трапеция Найти среднюю линию трапеции В А
- 27. Повторение Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то
- 28. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 9,5. E,F – середины диагоналей. Найти EF. В А D
- 29. Повторение Средняя линия трапеции равна полусумме оснований трапеции Средняя линия треугольника равна половине третьей стороны треугольника
- 30. Модуль «ГЕОМЕТРИЯ» №10 Повторение (2) Ответ: 13. АВСD – трапеция, АВ=23, CD=3. Найти МК. В А
- 31. Повторение Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны Средняя линия трапеции
- 32. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 2,5. АВСD – трапеция, P∆ABCD =100. Найти r. В А
- 33. Повторение Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны Радиус окружности, проведенный
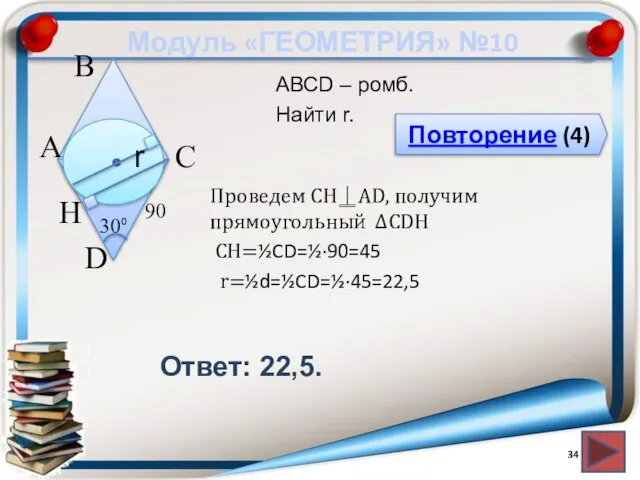
- 34. Модуль «ГЕОМЕТРИЯ» №10 Повторение (4) Ответ: 22,5. АВСD – ромб. Найти r. В А D С
- 35. Повторение Радиус окружности, проведенный в точку касания перпендикулярен касательной Перпендикуляры между параллельными прямыми равны В прямоугольном
- 36. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 8. Найти r. В А С r 11 По теореме
- 37. Повторение Прямой угол, вписанный в окружность опирается на диаметр окружности В прямоугольном треугольнике квадрат гипотенузы равен
- 38. Модуль «ГЕОМЕТРИЯ» №10 Повторение (3) Ответ: 6. АВСD – трапеция, P∆ABCD =12. Найти боковую сторону трапеции.
- 39. Повторение Средняя линия трапеции равна полусумме оснований трапеции Описать окружность можно только около равнобедренной трапеции Периметр
- 41. Скачать презентацию



































 Презентация на тему Аксиома параллельных прямых
Презентация на тему Аксиома параллельных прямых  Презентация на тему ЗАДАЧИ НА ДРОБИ
Презентация на тему ЗАДАЧИ НА ДРОБИ 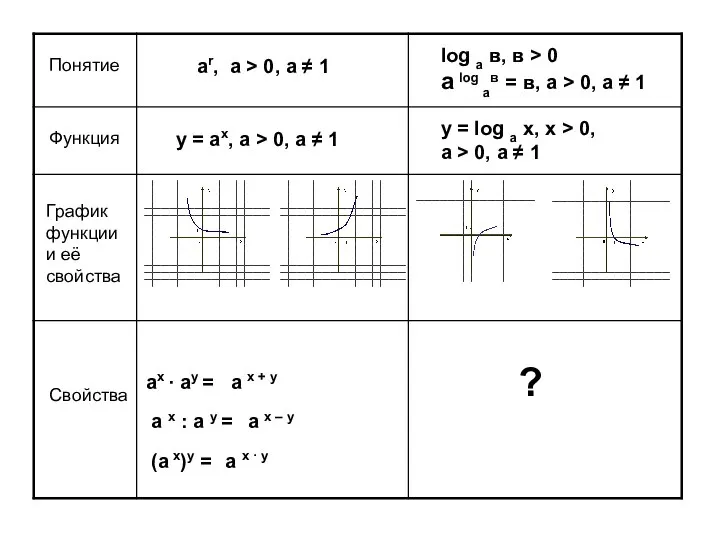 Свойства логарифмов
Свойства логарифмов Устный счёт. Состав числа 6. 1 класс
Устный счёт. Состав числа 6. 1 класс Sluchaynye_velichiny_14_sen
Sluchaynye_velichiny_14_sen Действительный анализ
Действительный анализ Математика. Задания по учебнику
Математика. Задания по учебнику Математическая викторина
Математическая викторина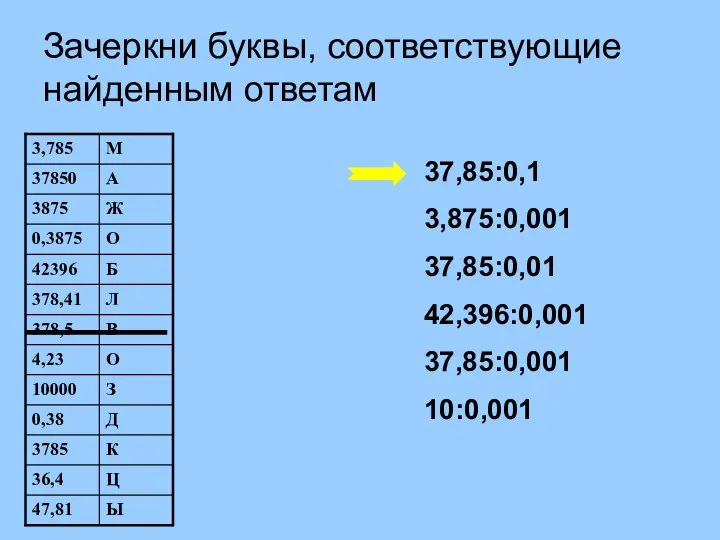 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности
Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Последовательности Задачи на готовых чертежах: Перпендикулярность плоскостей
Задачи на готовых чертежах: Перпендикулярность плоскостей Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Разминка. Подготовка к ГИА
Разминка. Подготовка к ГИА Площадь параллелограмма
Площадь параллелограмма Сравнение чисел
Сравнение чисел Комбинаторика
Комбинаторика Презентация на тему Линейная функция 6 класс
Презентация на тему Линейная функция 6 класс  Задачи на кратное сравнение
Задачи на кратное сравнение Градусная мера дуги окружности. Теорема о вписанном угле
Градусная мера дуги окружности. Теорема о вписанном угле Геометриялық фигуралар
Геометриялық фигуралар Презентация по математике "Табличное умножение и деление" -
Презентация по математике "Табличное умножение и деление" -  Квадратные корни. 8 класс
Квадратные корни. 8 класс Психолого – педагогические основы организации математического развития младших школьников
Психолого – педагогические основы организации математического развития младших школьников Базіс лінейнай прасторы. Каардынаты
Базіс лінейнай прасторы. Каардынаты Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс Функции и их графики. 9 класс
Функции и их графики. 9 класс Задачи на нахождение неизвестного
Задачи на нахождение неизвестного