Содержание
- 2. Оглавление 1.1 ТОЧКА Проецирование точки на плоскости проекций Точка на комплексном чертеже 1.2 ПРЯМАЯ Следы прямой
- 3. Точка на плоскости
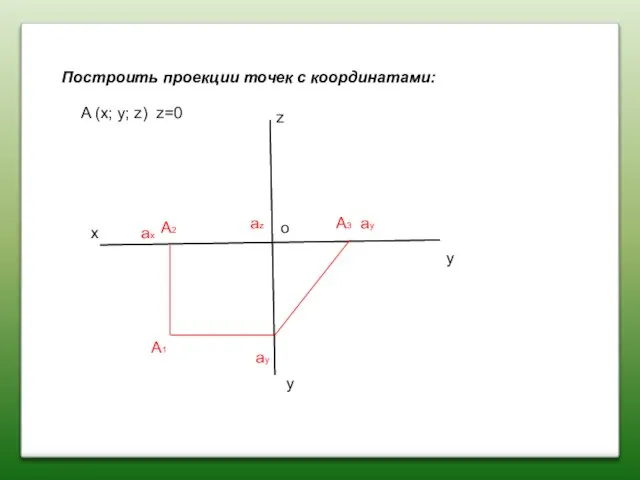
- 4. Построить проекции точек с координатами: x z y y A (x; y; z) z=0 A2 A1
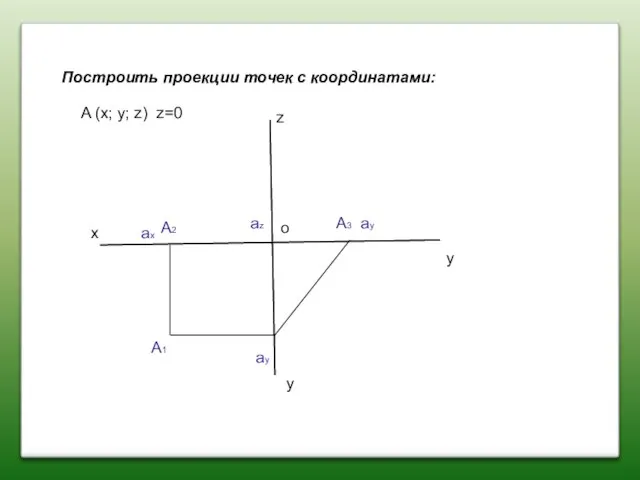
- 5. Построить проекции точек с координатами: x z y y A (x; y; z) z=0 A2 A1
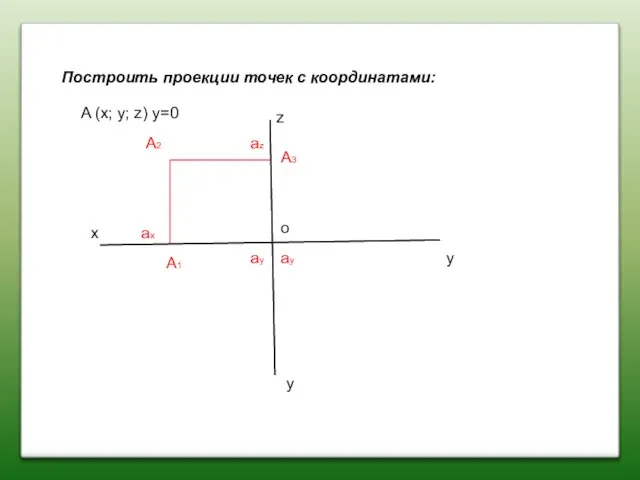
- 6. Построить проекции точек с координатами: x z y y A (x; y; z) y=0 A2 A1
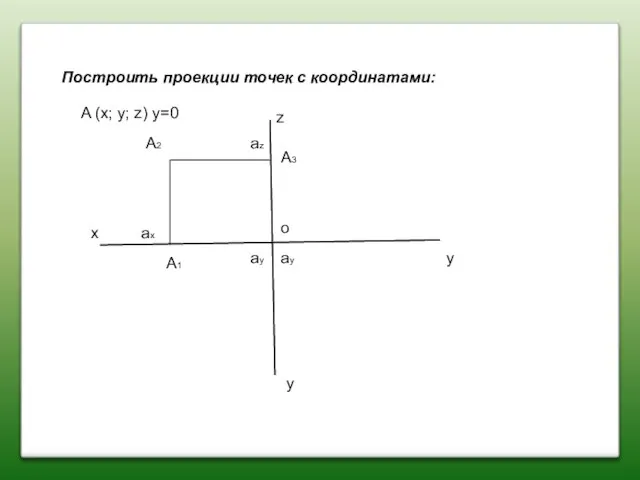
- 7. Построить проекции точек с координатами: x z y y A (x; y; z) y=0 A2 A1
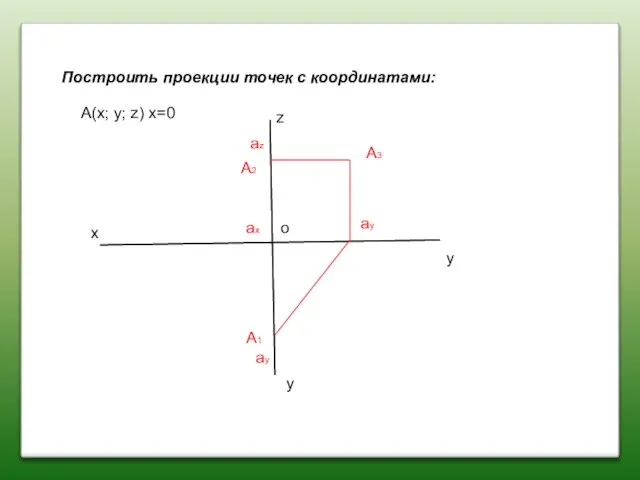
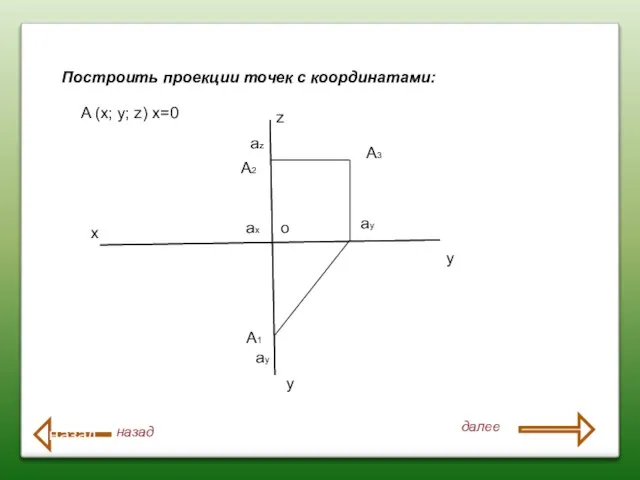
- 8. Построить проекции точек с координатами: x z y y A(x; y; z) x=0 A2 A1 A3
- 9. Построить проекции точек с координатами: x z y y A (x; y; z) x=0 A2 A1
- 10. Точка на комплексном чертеже Точка на комплексном чертеже
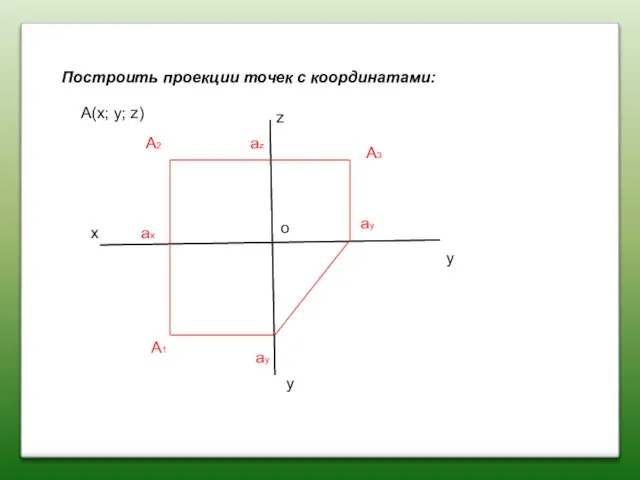
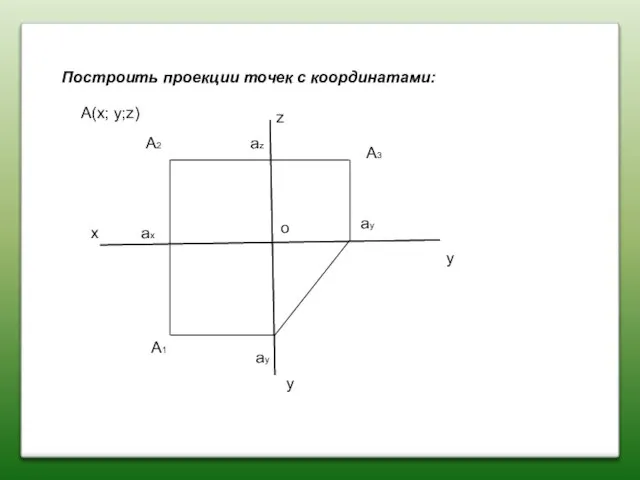
- 11. Построить проекции точек с координатами: x z y y A(x; y; z) A2 A1 A3 ax
- 12. Построить проекции точек с координатами: x z y y A(x; y;z) A2 A1 A3 ax az
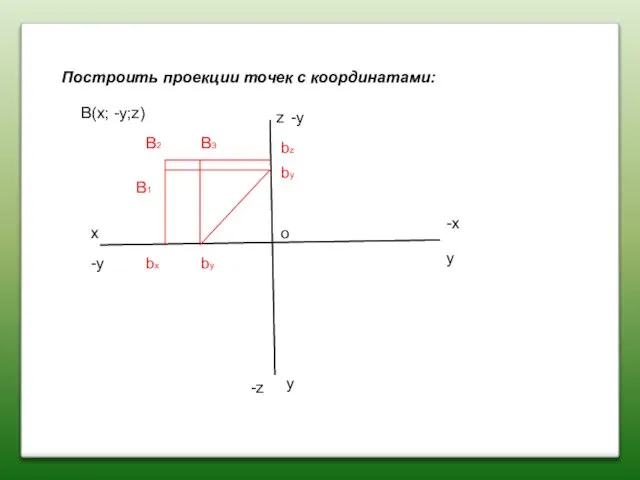
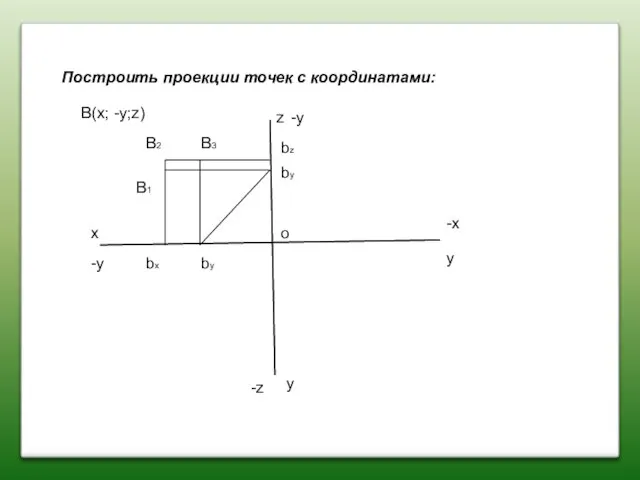
- 13. Построить проекции точек с координатами: x z y y B(x; -y;z) B2 B1 B3 bx bz
- 14. Построить проекции точек с координатами: x z y y B(x; -y;z) B2 B1 B3 bx bz
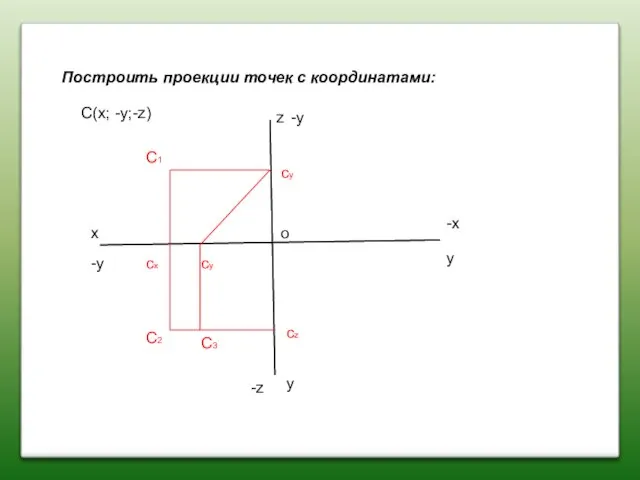
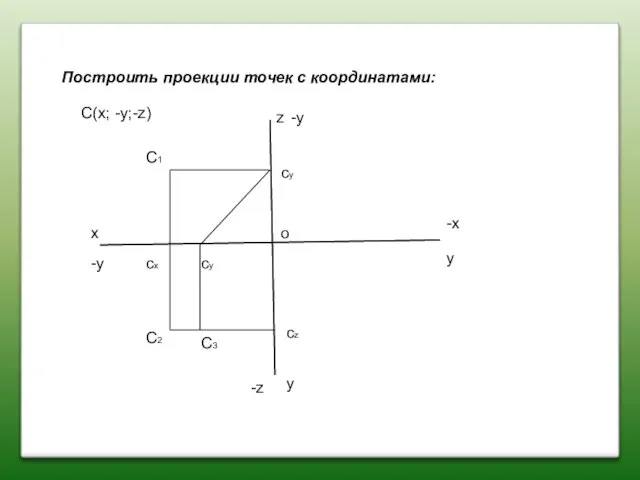
- 15. Построить проекции точек с координатами: x z y y C(x; -y;-z) C2 C1 C3 cx cz
- 16. Построить проекции точек с координатами: x z y y C(x; -y;-z) C2 C1 C3 cx cz
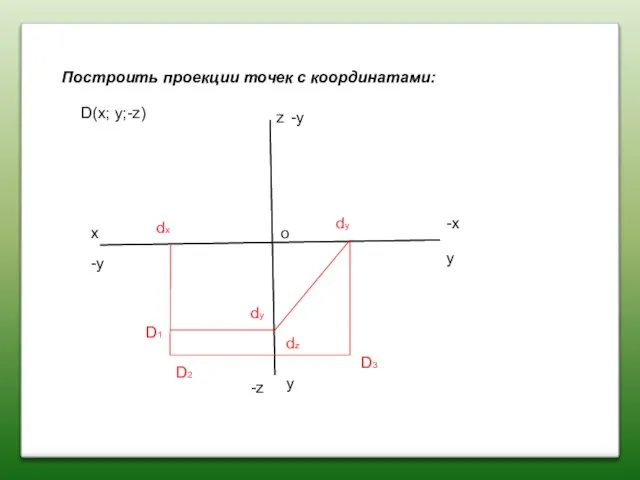
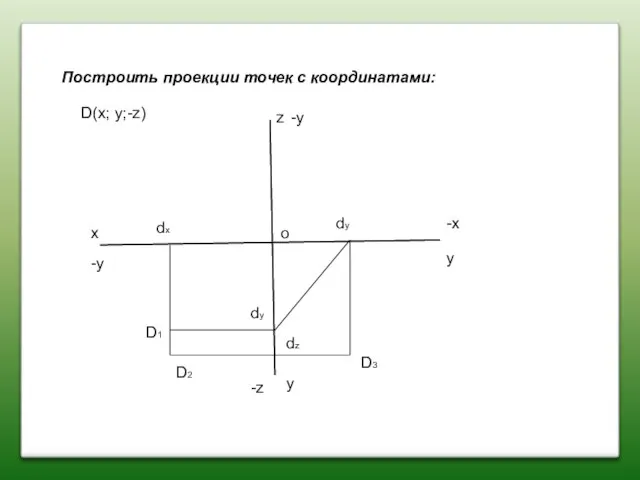
- 17. Построить проекции точек с координатами: x z y y D(x; y;-z) D2 D1 D3 dx dz
- 18. Построить проекции точек с координатами: x z y y D(x; y;-z) D2 D1 D3 dx dz
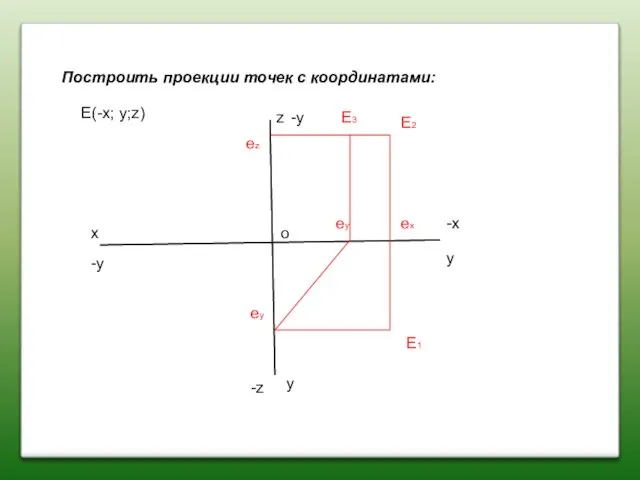
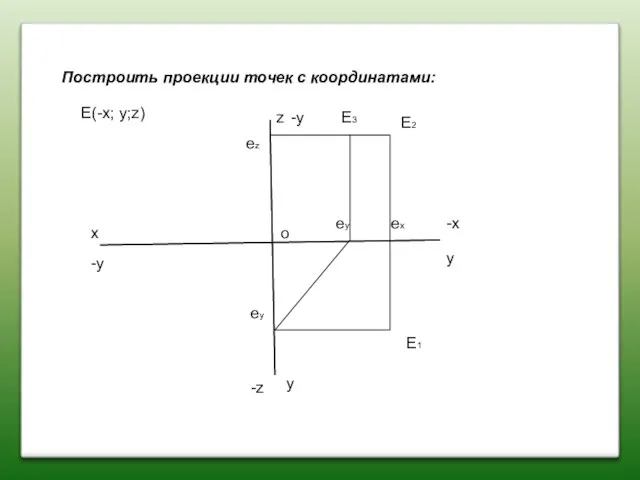
- 19. Построить проекции точек с координатами: x z y y E(-x; y;z) E2 E1 E3 ex ez
- 20. Построить проекции точек с координатами: x z y y E(-x; y;z) E2 E1 E3 ex ez
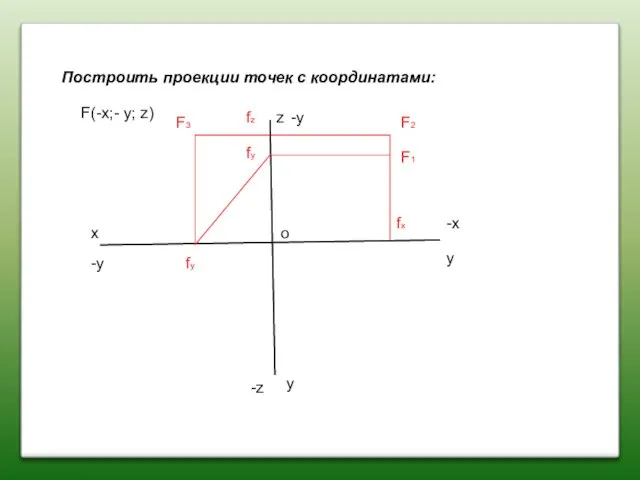
- 21. Построить проекции точек с координатами: x z y y F(-x;- y; z) F2 F1 F3 fx
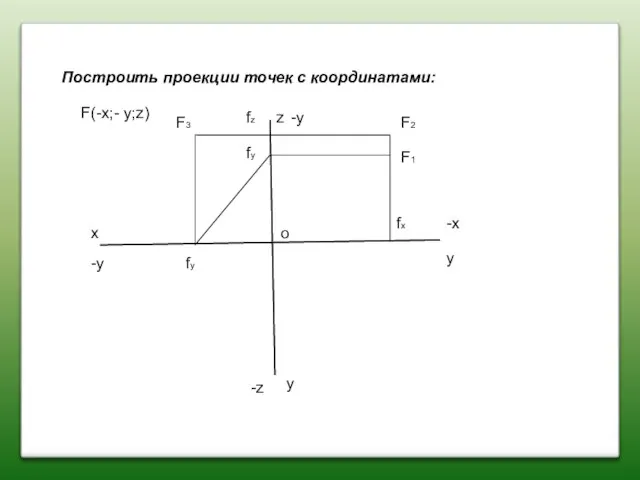
- 22. Построить проекции точек с координатами: x z y y F(-x;- y;z) F2 F1 F3 fx fz
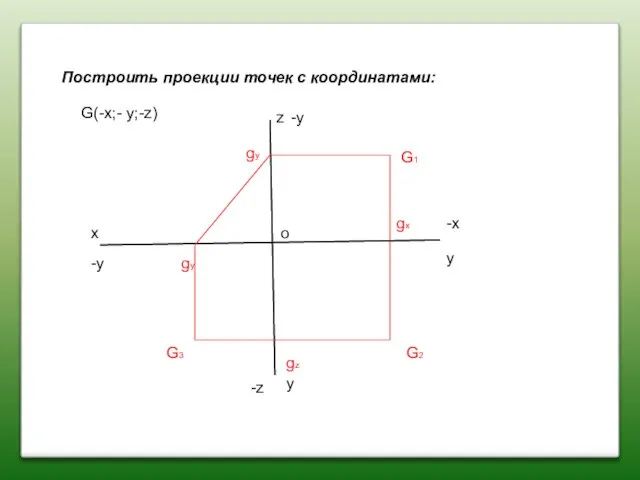
- 23. Построить проекции точек с координатами: x z y y G(-x;- y;-z) G2 G1 G3 gx gz
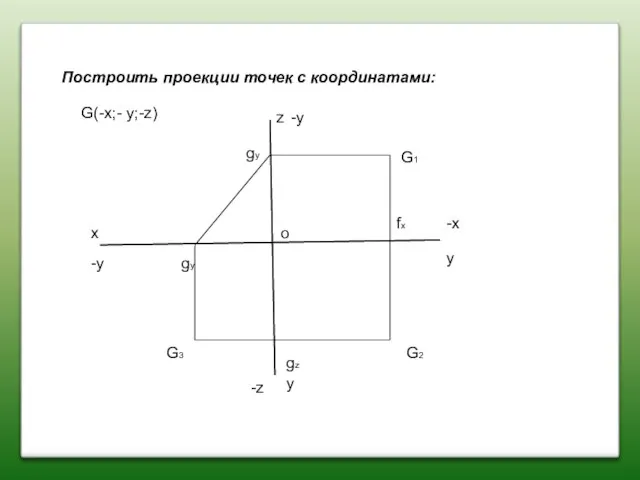
- 24. Построить проекции точек с координатами: x z y y G(-x;- y;-z) G2 G1 G3 fx gz
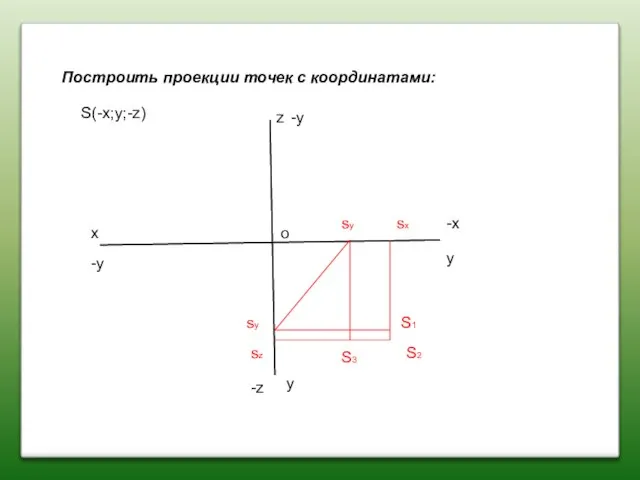
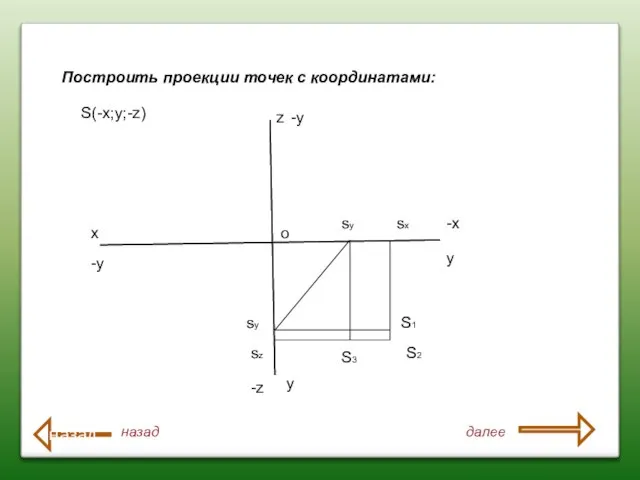
- 25. Построить проекции точек с координатами: x z y y S(-x;y;-z) S2 S1 S3 sx sz sy
- 26. Построить проекции точек с координатами: x z y y S(-x;y;-z) S2 S1 S3 sx sz sy
- 27. Точка на комплексном чертеже Следы прямой
- 28. ЗАДАЧА Построить следы прямой АВ, покапать видимость прямой, дать характеристики положения прямой в пространстве относительно плоскостей
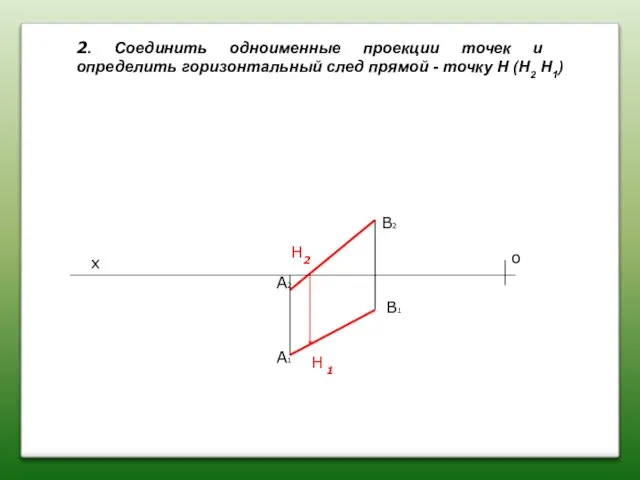
- 29. А2 А1 В2 В1 х о 2. Соединить одноименные проекции точек и определить горизонтальный след прямой
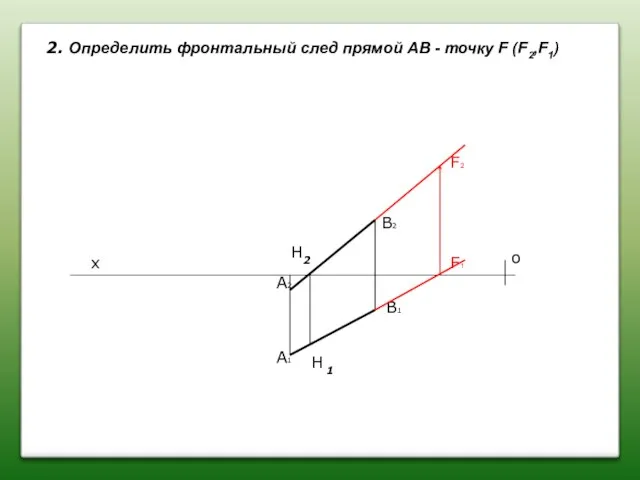
- 30. А2 А1 В2 В1 х о 2. Определить фронтальный след прямой АВ - точку F (F2,F1)
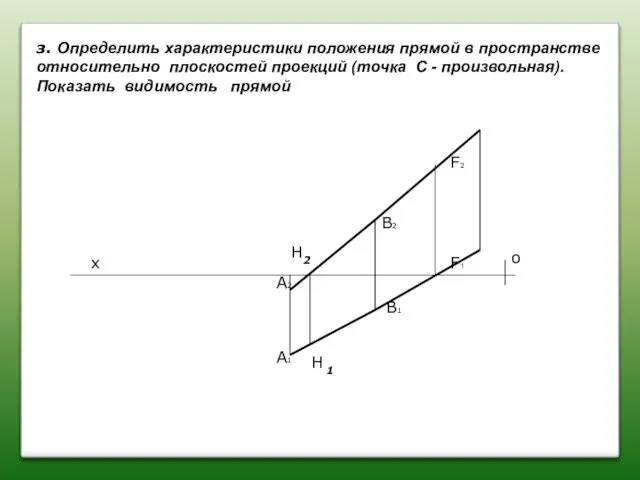
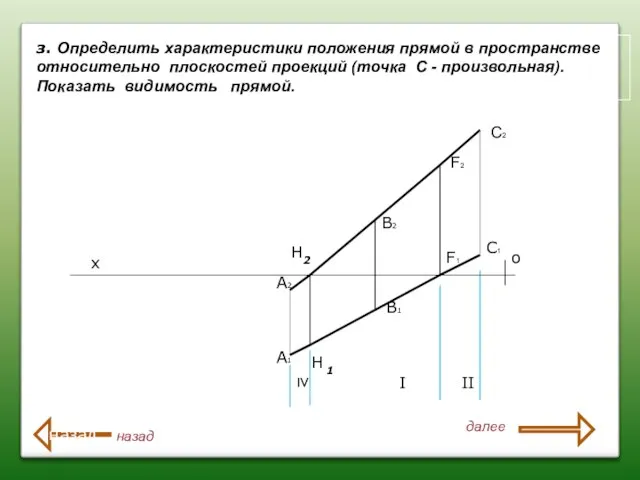
- 31. А2 А1 В2 В1 х о з. Определить характеристики положения прямой в пространстве относительно плоскостей проекций
- 32. А2 А1 В2 В1 х о з. Определить характеристики положения прямой в пространстве относительно плоскостей проекций
- 33. Точка на комплексном чертеже Определение истинной величины отрезка прямой и углов наклона прямой к плоскостям проекций
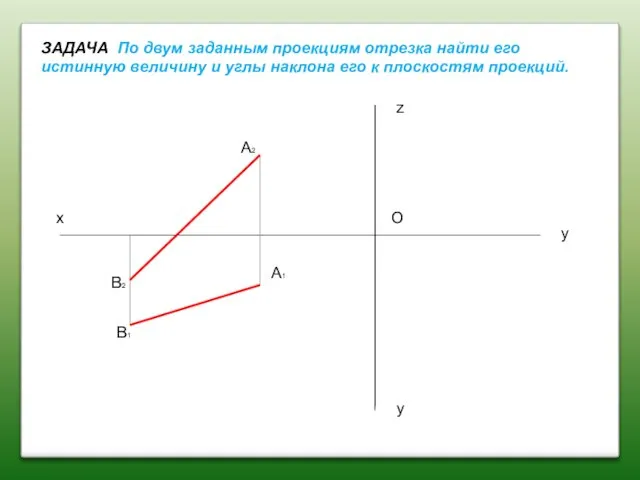
- 34. ЗАДАЧА По двум заданным проекциям отрезка найти его истинную величину и углы наклона его к плоскостям
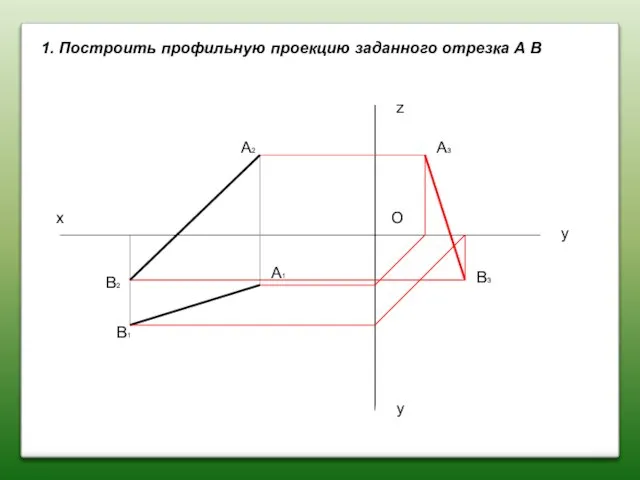
- 35. 1. Построить профильную проекцию заданного отрезка А В О х у z y А1 А2 В1
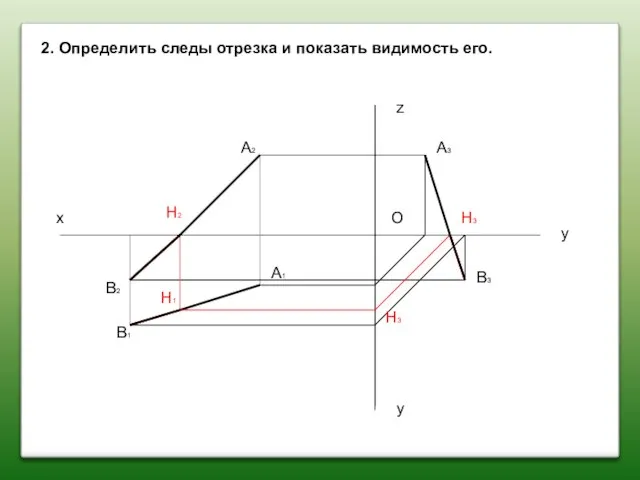
- 36. 2. Определить следы отрезка и показать видимость его. О х у z y А1 А2 В1
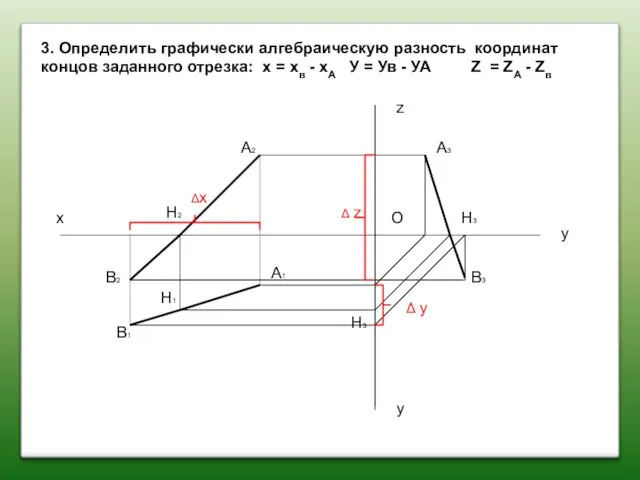
- 37. 3. Определить графически алгебраическую разность координат концов заданного отрезка: х = хв - хА У =
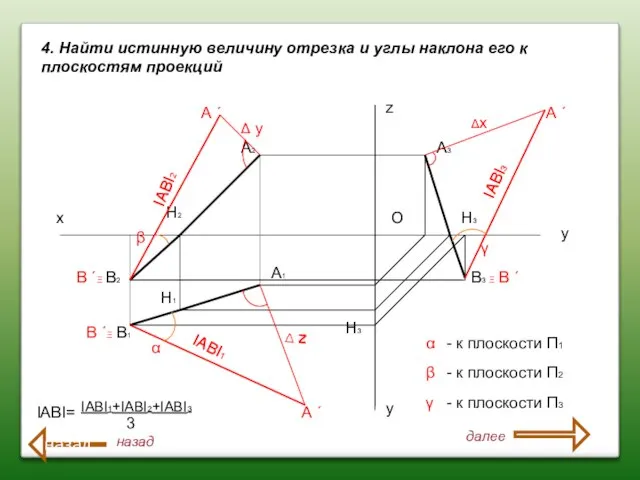
- 38. 4. Найти истинную величину отрезка и углы наклона его к плоскостям проекций О х у z
- 39. Точка на комплексном чертеже Следы плоскости
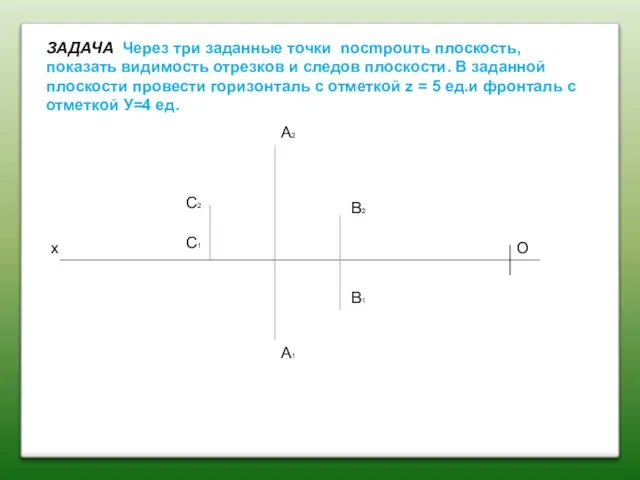
- 40. ЗАДАЧА Через три заданные точки nоcmроuть плоскость, показать видимость отрезков и следов плоскости. В заданной плоскости
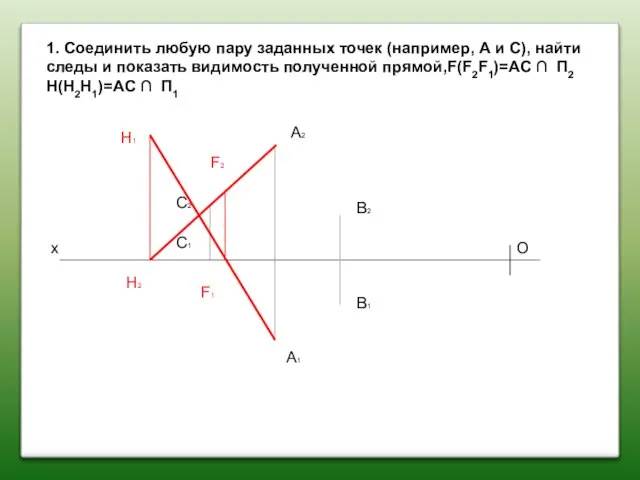
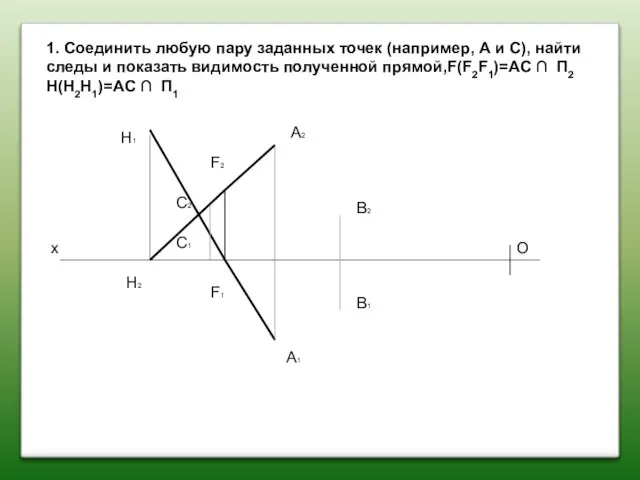
- 41. 1. Соединить любую пару заданных точек (например, А и С), найти следы и показать видимость полученной
- 42. 1. Соединить любую пару заданных точек (например, А и С), найти следы и показать видимость полученной
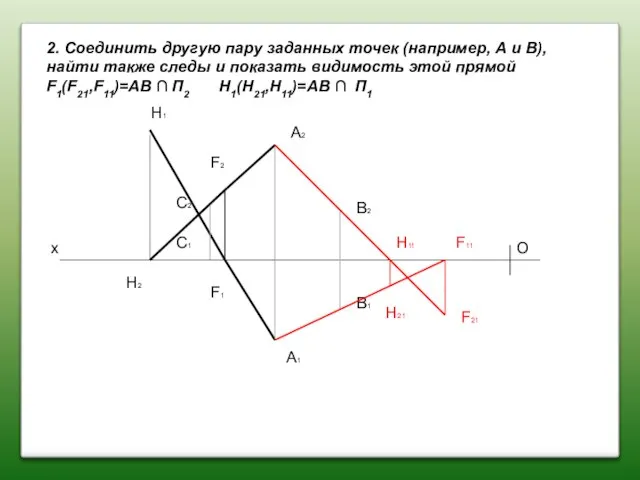
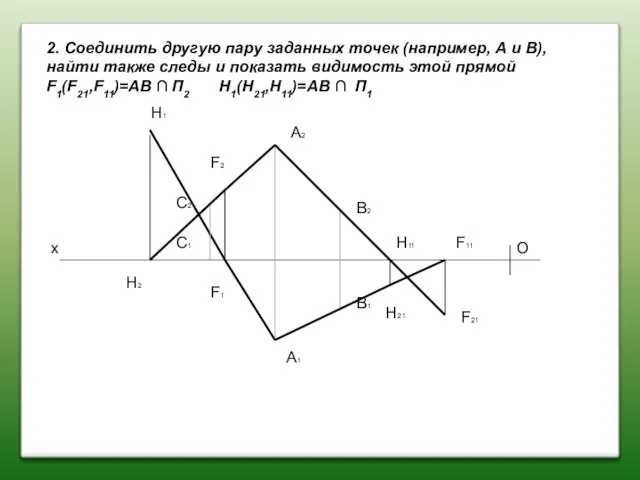
- 43. 2. Соединить другую пару заданных точек (например, А и В), найти также следы и показamь видимость
- 44. 2. Соединить другую пару заданных точек (например, А и В), найти также следы и показamь видимость
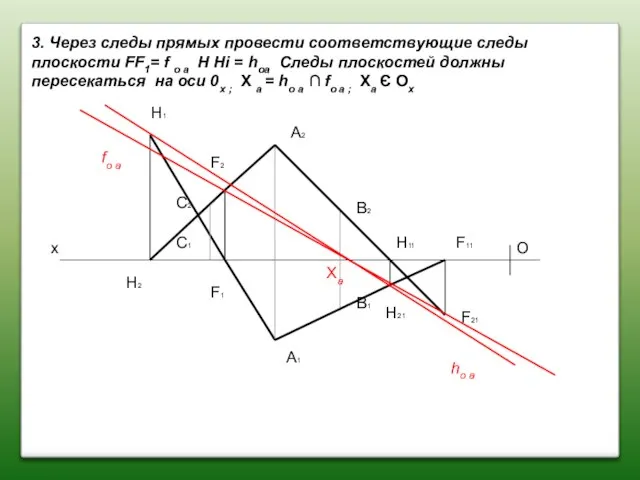
- 45. 3. Через следы прямых провести соответствующие следы плоскости FF1= f o а Н Hi = hoа
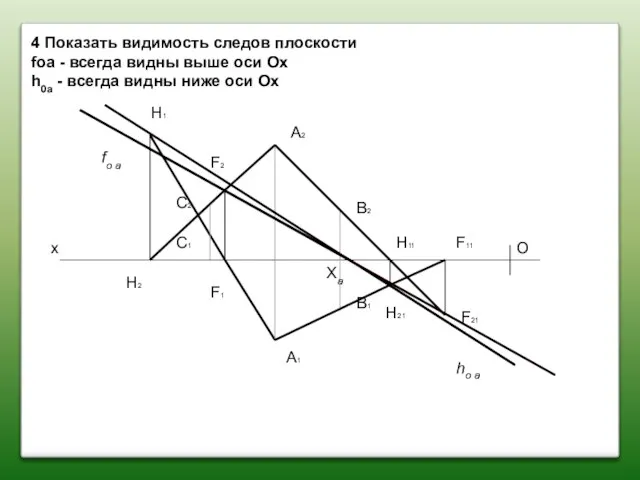
- 46. 4 Показать видимость следов плоскости foa - всегда видны выше оси Ох h0а - всегда видны
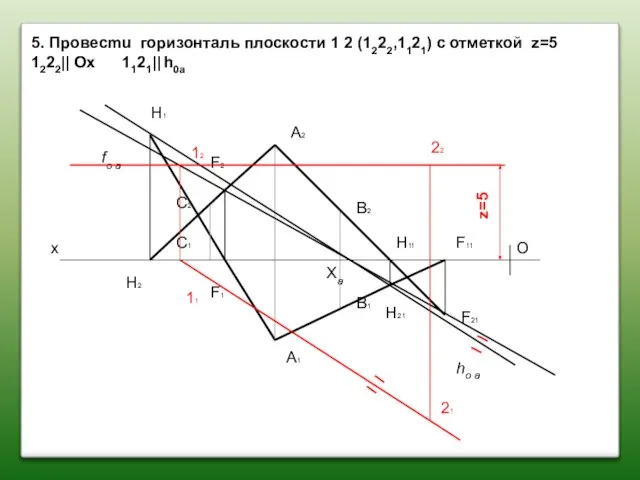
- 47. 5. Пpoвecmu горизонталь плоскости 1 2 (1222,1121) с отметкой z=5 1222|| Ох 1121|| h0a О х
- 48. 6. Провесmи фронталь плоскости 34(3242;3141) С отметкой у=4 3141 || 0х 3242 || foа О х
- 49. Точка на комплексном чертеже Пересечение двух плоскостей (плоскости общего положения)
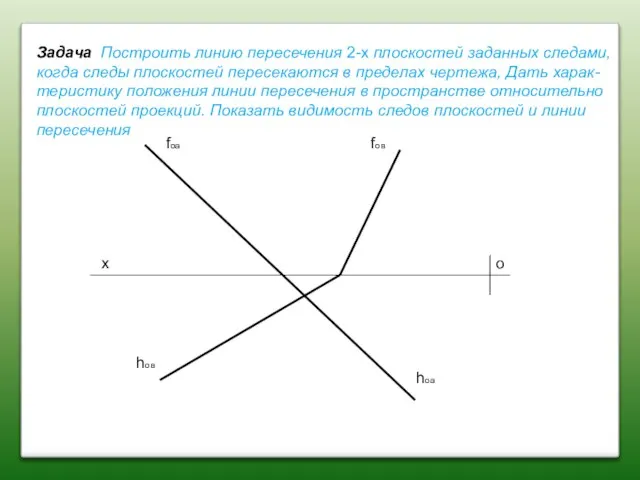
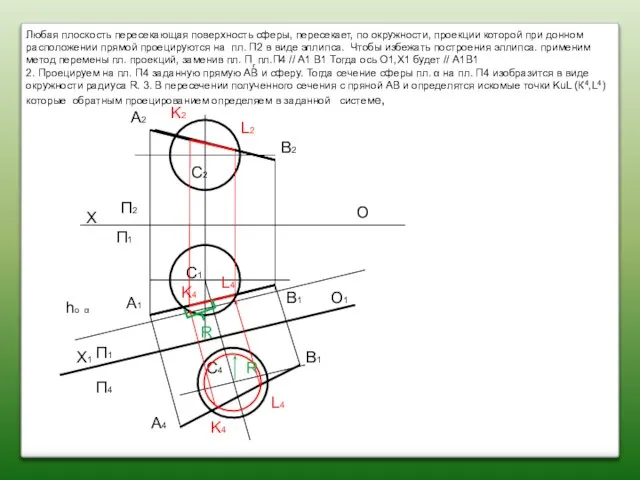
- 50. Задача Построить линию пересечения 2-х плоскостей заданных следами, когда следы плоскостей пересекаются в пределах чертежа, Дать
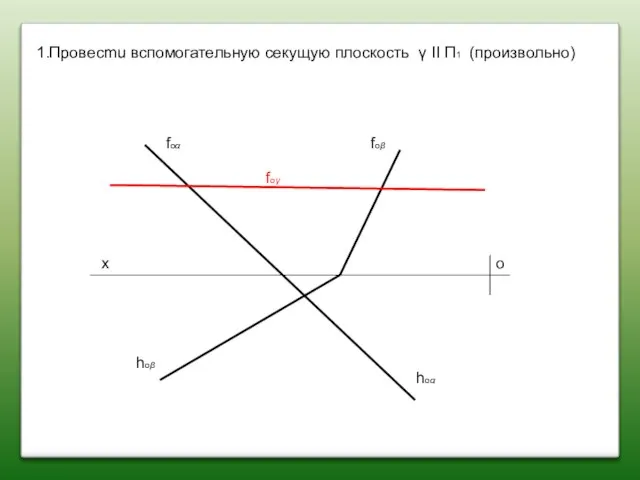
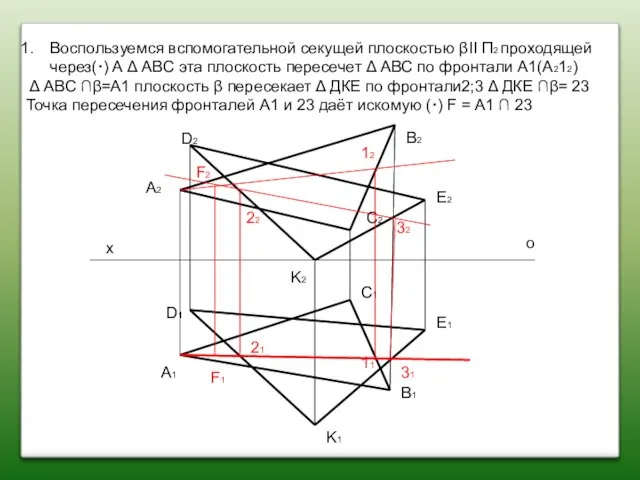
- 51. 1.Пpoвecmu вспомогательную секущую плоскость γ II П1 (произвольно) х о foα foβ hoβ hoα foγ
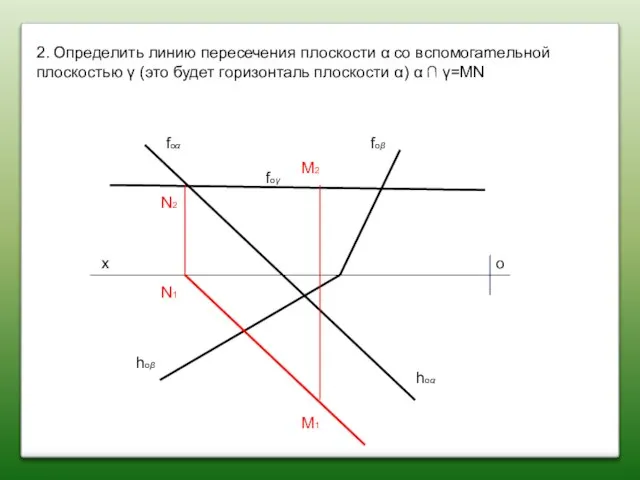
- 52. 2. Определить линию пересечения плоскости α со вспомогamельной плоскостью γ (это будет горизонталь плоскости α) α
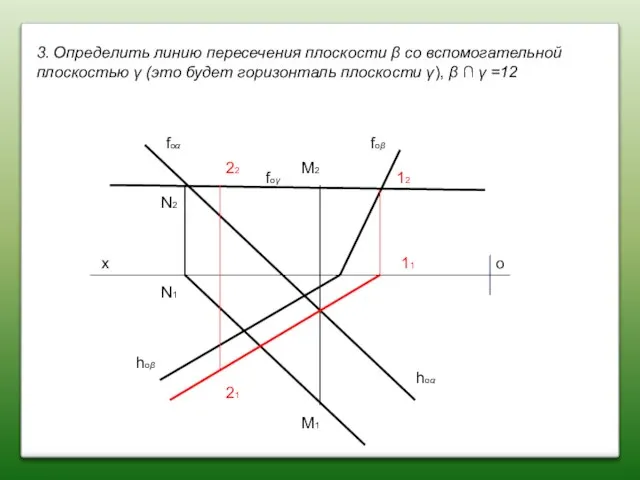
- 53. 3. Определить линию пересечения плоскости β со вспомoгательной плоскостью γ (это будет горизонталь плоскости γ), β
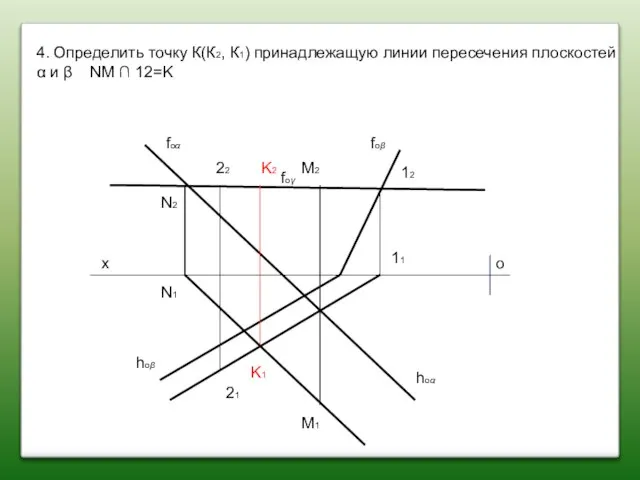
- 54. 4. Определить точку К(К2, К1) принадлежащую линии пересечения плоскостей α и β NM ∩ 12=K х
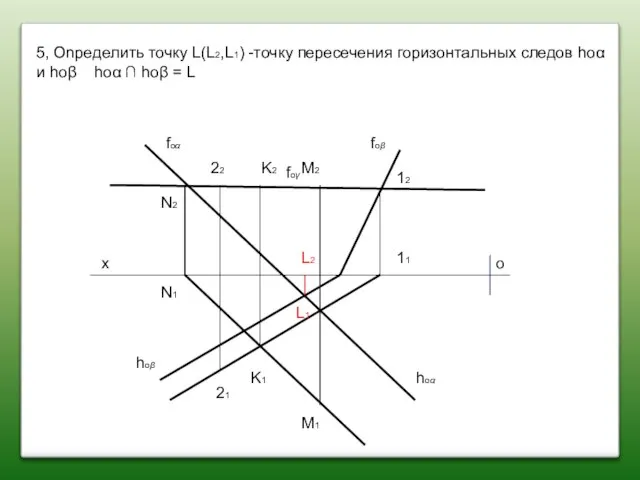
- 55. 5, Onределить точку L(L2,L1) -точку пересечения горизонтальных следов hoα и hoβ hoα ∩ hoβ = L
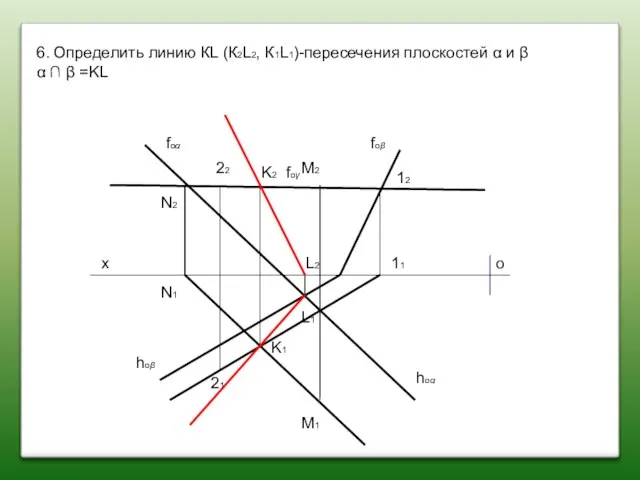
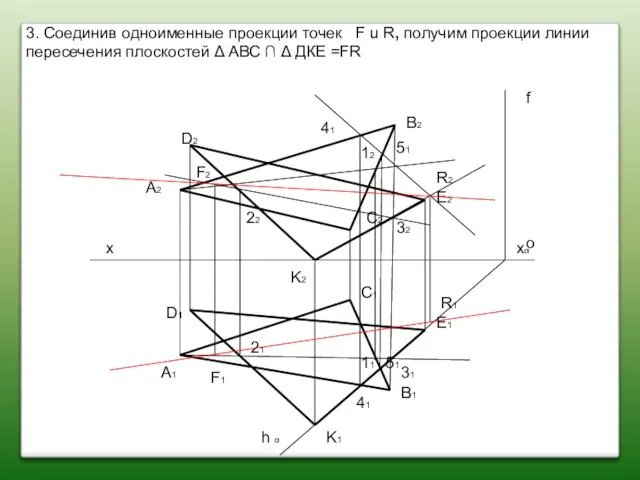
- 56. 6. Определить линию КL (К2L2, К1L1)-пересечения плоскостей α и β α ∩ β =KL х о
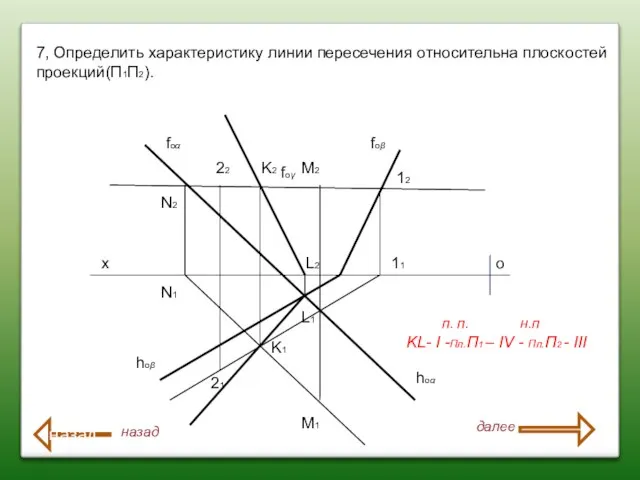
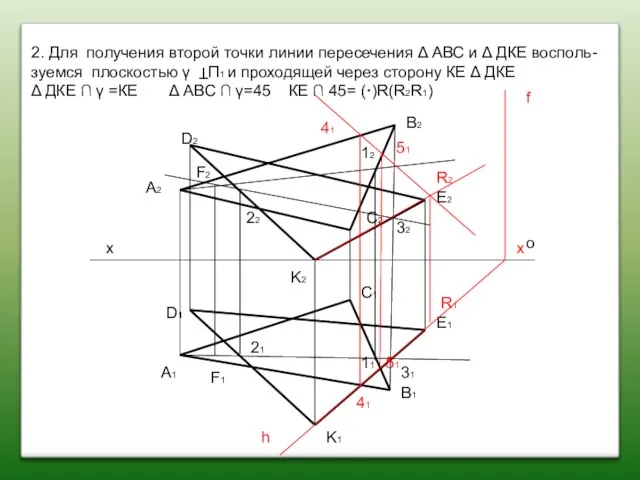
- 57. 7, Определить характеристику линии пересечения относительна плоскостей проекций(П1П2). х о foα foβ hoβ hoα foγ N2
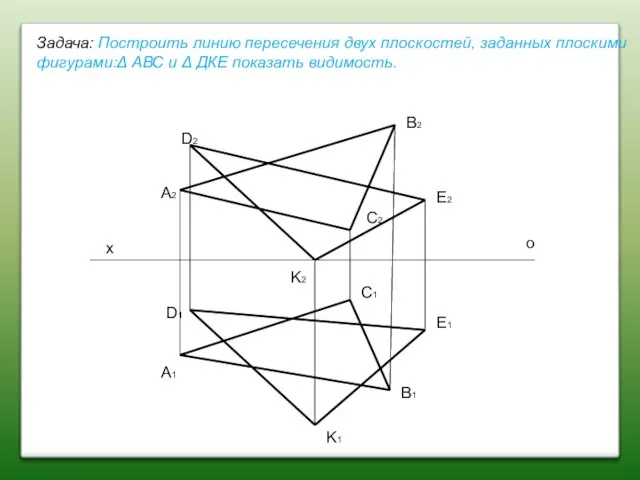
- 58. Точка на комплексном чертеже Пересечение двух плоскостей (Заданных геометрическими фигурами )
- 59. x o A2 A1 D1 D2 B2 B1 C2 C1 E2 E1 K2 K1 Задача: Построить
- 60. x o A2 A1 D1 D2 B2 B1 C2 C1 E2 E1 K2 K1 F1 F2
- 61. x o A2 A1 D1 D2 B2 B1 C2 C1 E2 E1 K2 K1 F1 F2
- 62. x o A2 A1 D1 D2 B2 B1 C2 C1 E2 E1 K2 K1 F1 F2
- 63. x o A2 A1 D1 D2 B2 B1 C2 C1 E2 E1 K2 K1 F1 F2
- 64. x o A2 A1 D1 D2 B2 B1 C2 C1 E2 E1 K2 K1 F1 F2
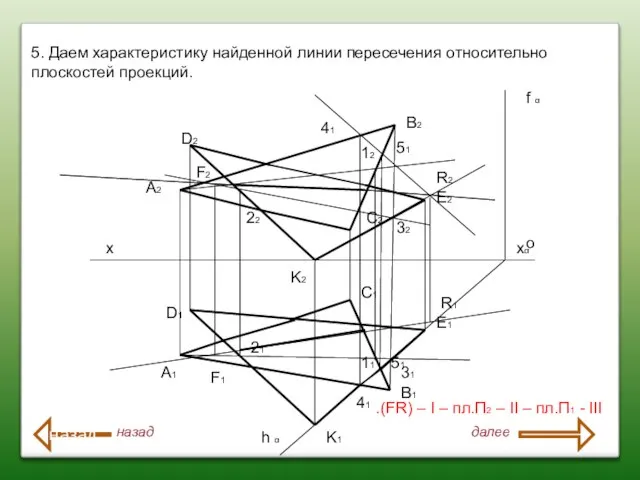
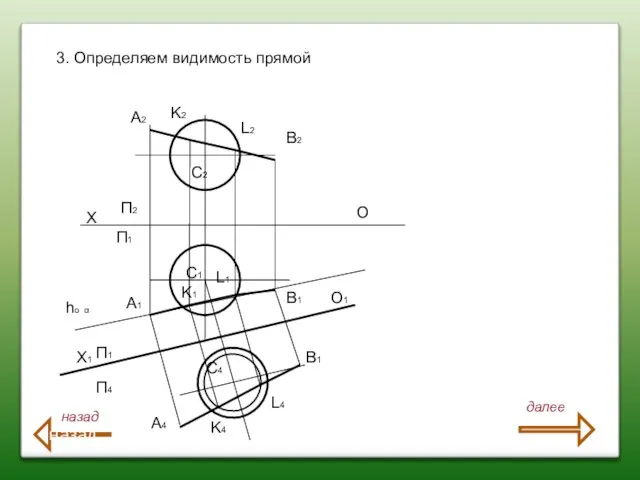
- 65. Точка на комплексном чертеже Точка встречи прямой с плоскостью общего положения , определение видимости прямой относительно
- 66. Задача: определить точку пересечения прямой EF с плоскостью , заданной плоскостью фигуры - треугольником АВС показать
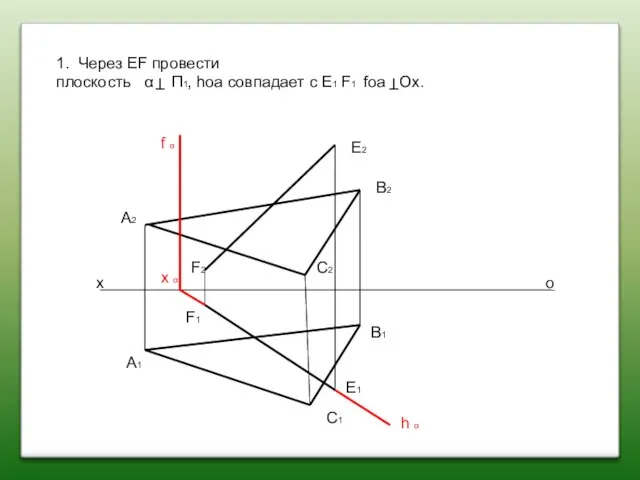
- 67. 1. Через EF провести плоскость α П1, hоa совпадает с Е1 F1 fоa Ox. х о
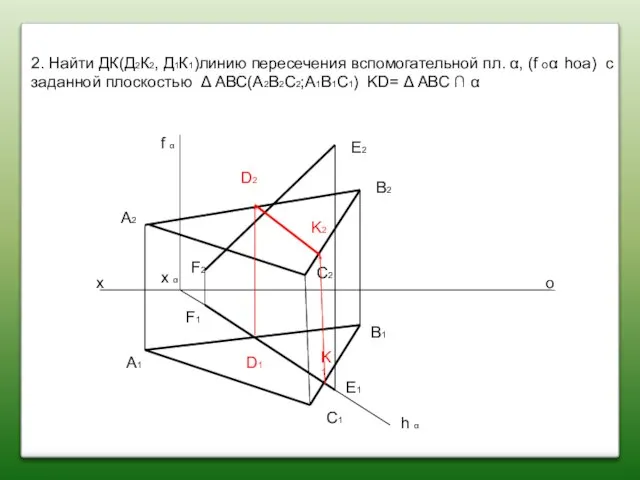
- 68. 2. Найти ДК(Д2К2, Д1К1)линию пересечения вспомогательной пл. α, (f оα hoa) с заданной плоскостью Δ АВС(А2В2С2;А1В1С1)
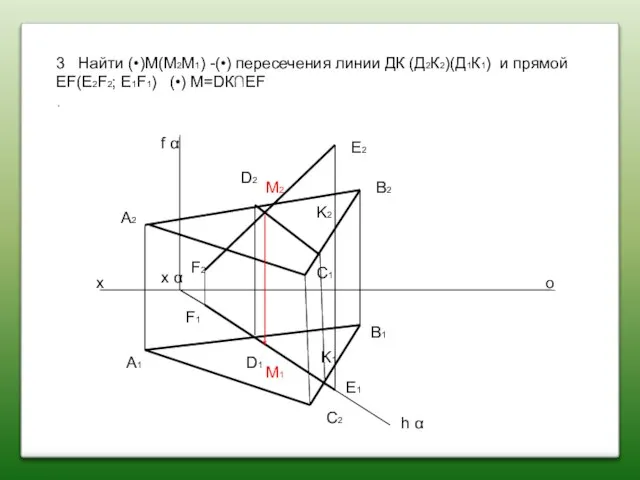
- 69. 3 Найти (•)М(M2M1) -(•) пересечения линии ДК (Д2К2)(Д1К1) и прямой EF(E2F2; E1F1) (•) M=DК∩EF . х
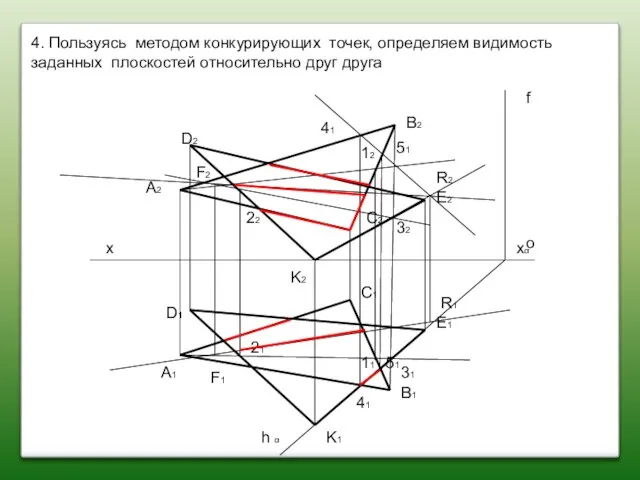
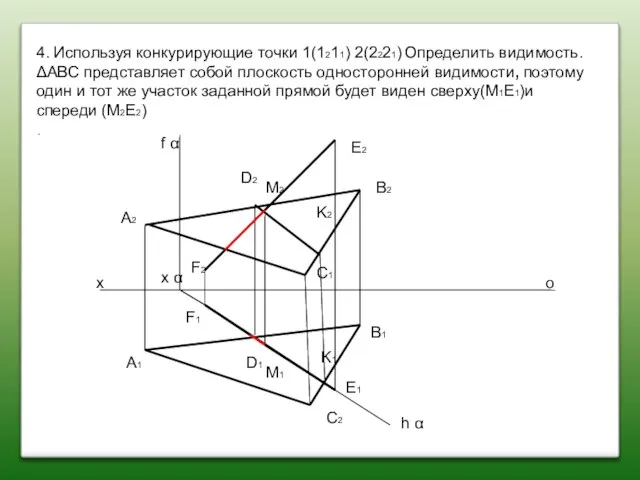
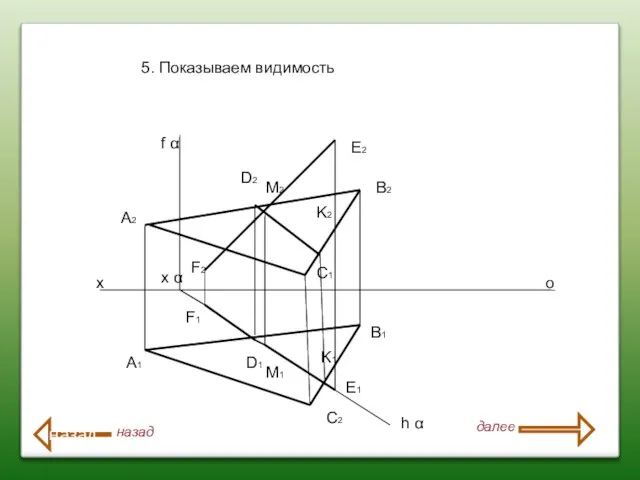
- 70. 4. Используя конкурирующие точки 1(1211) 2(2221) Определить видимость.ΔАВС представляет собой плоскость односторонней видимости, поэтому один и
- 71. х о А2 A1 F2 F1 B2 B1 C2 C1 E2 E1 x α f α
- 72. Точка на комплексном чертеже Пересечение прямой с геометрическими телами
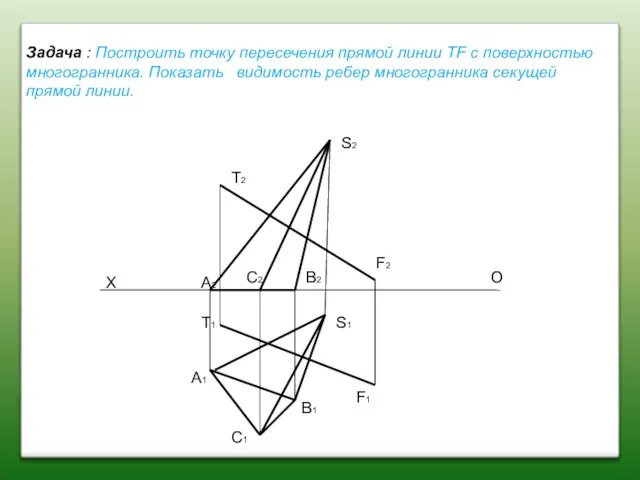
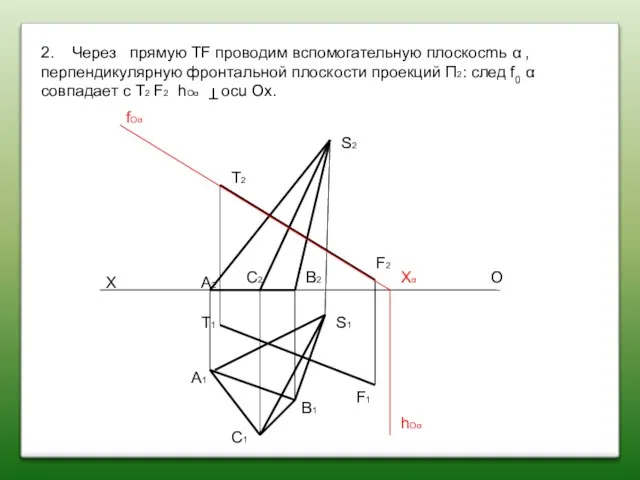
- 73. S2 S1 T2 T1 F2 F1 X O A2 A1 C2 C1 B2 B1 Задача :
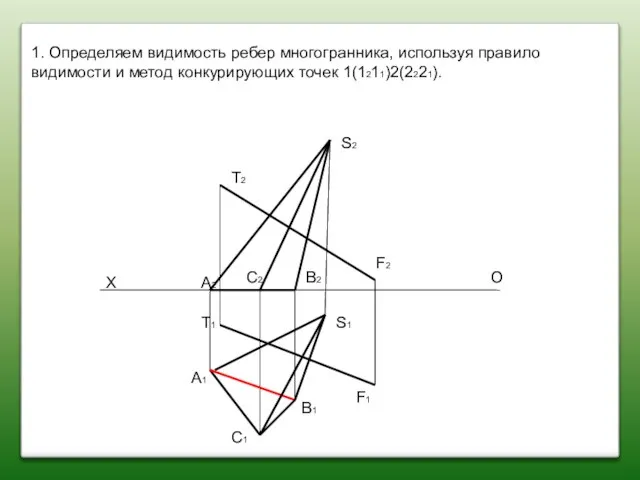
- 74. S2 S1 T2 T1 F2 F1 X O A2 A1 C2 C1 B2 B1 1. Определяем
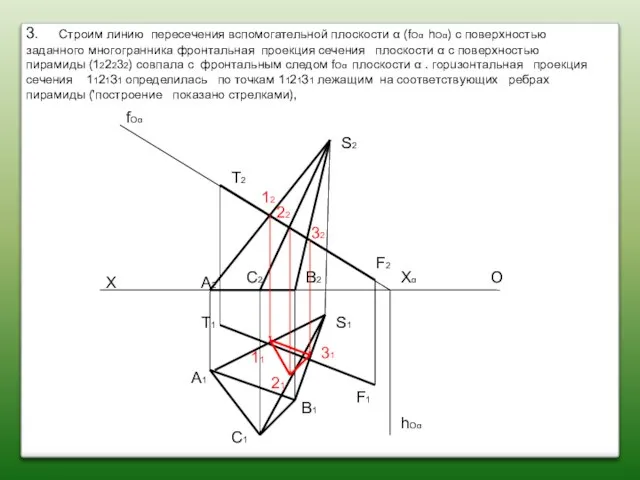
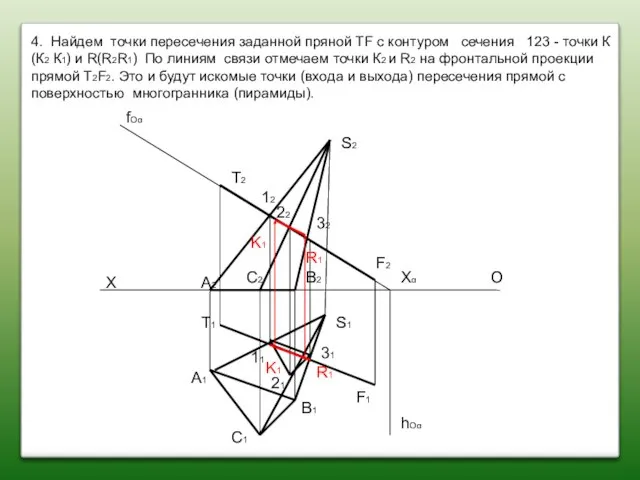
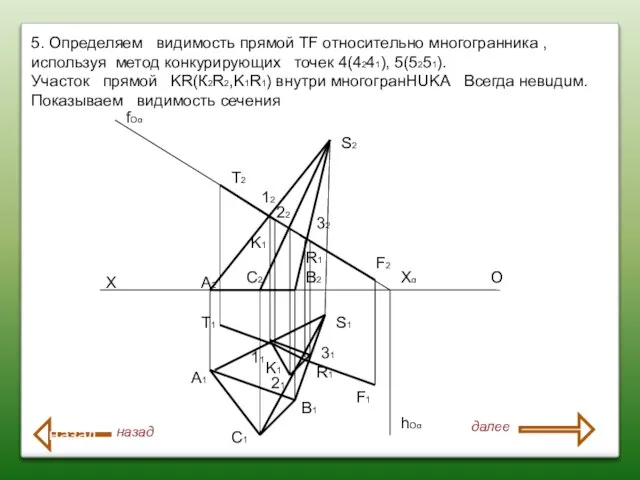
- 75. S2 S1 T2 T1 F2 F1 X O A2 A1 C2 C1 B2 B1 fOα hOα
- 76. S2 S1 T2 T1 F2 F1 X O A2 A1 C2 C1 B2 B1 fOα hOα
- 77. S2 S1 T2 T1 F2 F1 X O A2 A1 C2 C1 B2 B1 fOα hOα
- 78. S2 S1 T2 T1 F2 F1 X O A2 A1 C2 C1 B2 B1 fOα hOα
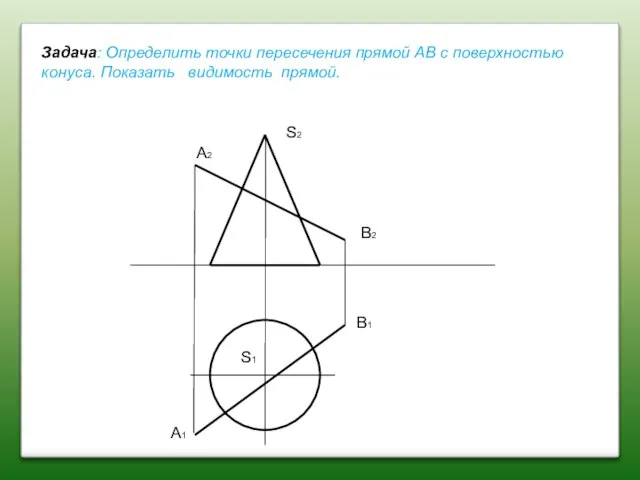
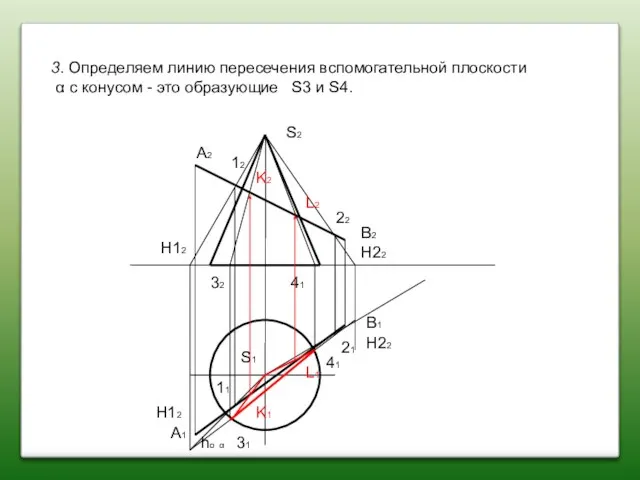
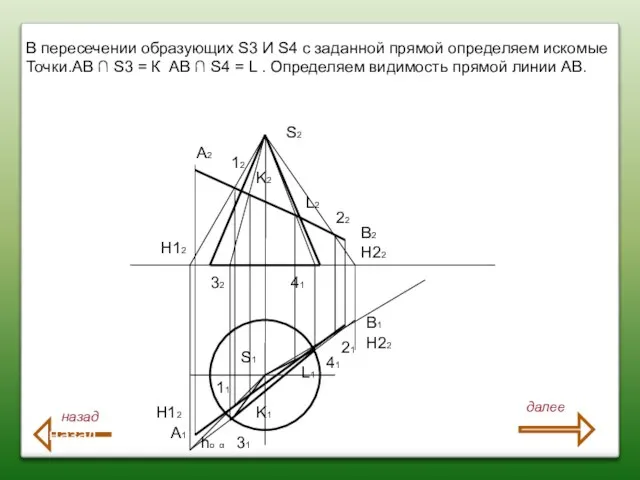
- 80. A2 A1 B2 B1 S2 S1 Задача: Определить точки пересечения прямой AВ с поверхностью конуса. Показать
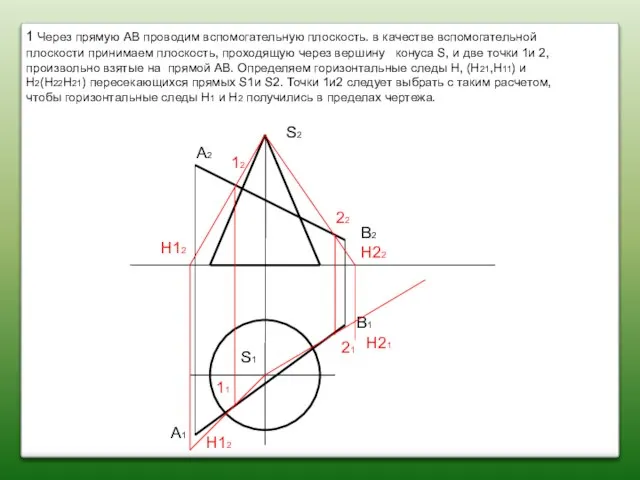
- 81. A2 A1 B2 B1 S2 S1 12 22 21 11 H12 H12 H22 H21 1 Через
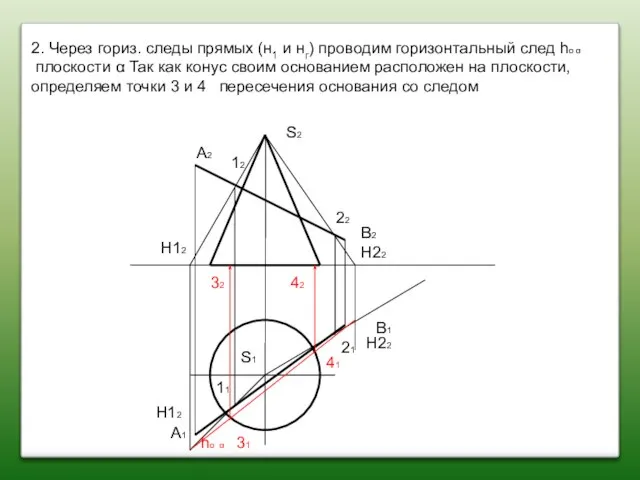
- 82. A2 A1 B2 B1 S2 S1 11 21 12 22 31 32 41 42 H12 H12
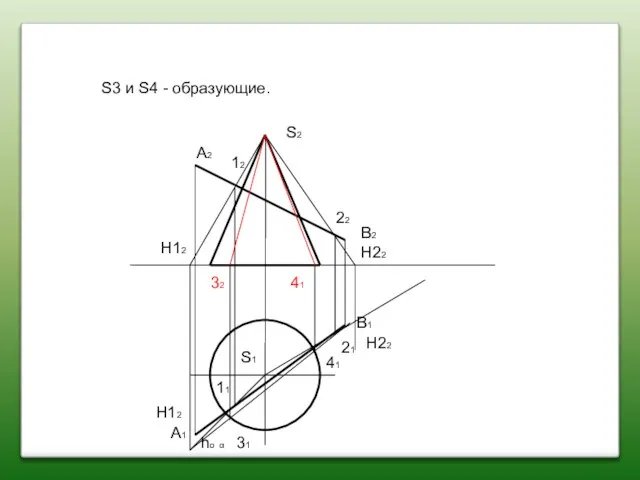
- 83. A2 A1 B2 B1 S2 S1 11 21 12 22 31 32 41 41 H12 H12
- 84. A2 A1 B2 B1 S2 S1 11 21 12 22 31 32 41 41 H12 H12
- 85. A2 A1 B2 B1 S2 S1 11 21 12 22 31 32 41 41 H12 H12
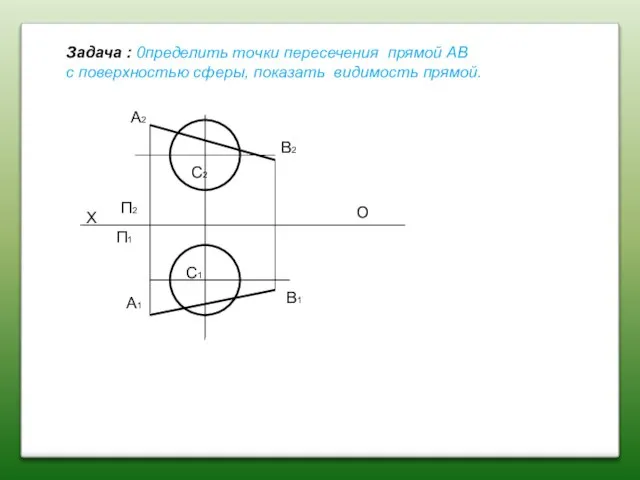
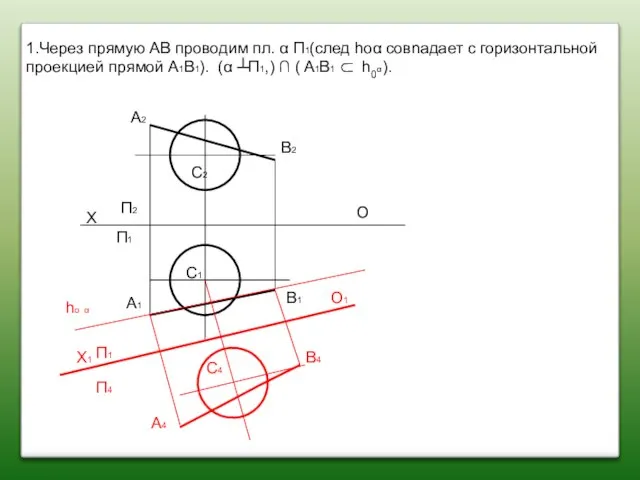
- 87. C2 C1 A2 A1 B2 B1 П2 П1 О Х Задача : 0пределить moчки пересечения прямой
- 88. ho α C2 C1 A2 A1 B2 B1 П2 П1 О Х Х1 П4 П1 О1
- 89. ho α C2 C1 A2 A1 B2 B1 П2 П1 О Х Х1 П4 П1 О1
- 90. ho α C2 C1 A2 A1 B2 B1 П2 П1 О Х Х1 П4 П1 О1
- 91. Точка на комплексном чертеже ЗАДАЧИ
- 92. Задача По заданным координатам точек А; В; С; D; E; F;G; К построить их горизонтальные, фронтальные
- 93. Задача Построить проекции отрезка прямой А В по заданным координатам его концов. Найти следы прямой. назад
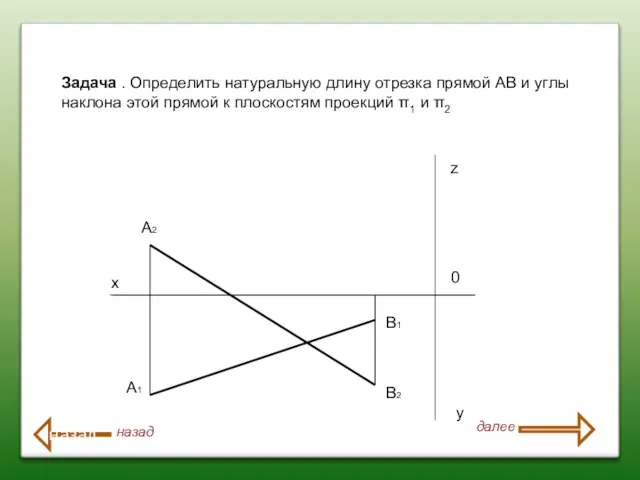
- 94. Задача . Определить натуральную длину отрезка прямой АВ и углы наклона этой прямой к плоскостям проекций
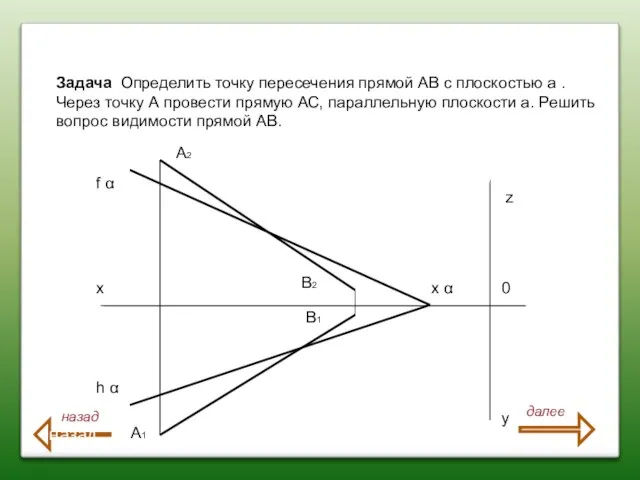
- 95. Задача Определить точку пересечения прямой АВ с плоскостью а . Через точку А провести прямую АС,
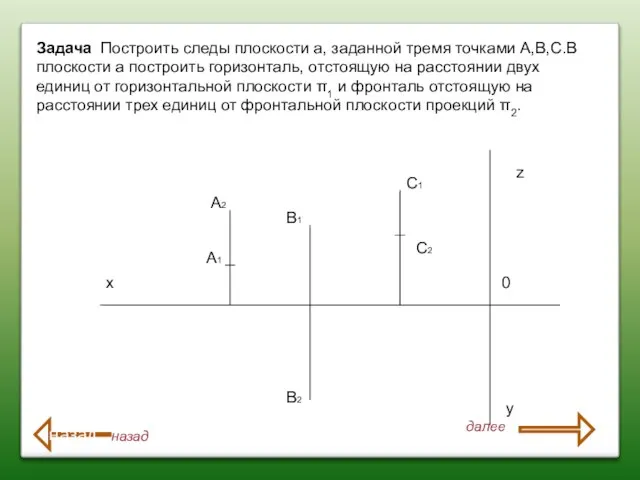
- 96. Задача Построить следы плоскости а, заданной тремя точками А,В,С.В плоскости а построить горизонталь, отстоящую на расстоянии
- 97. Задача По заданным координатам вершин построить проекции треугольников ABC и DEF. Определить линию их пересечения. Решить
- 99. Скачать презентацию



















 Презентация на тему Функция у=х^3 и её график
Презентация на тему Функция у=х^3 и её график  Комплексные числа. Определение множеств комплексных чисел
Комплексные числа. Определение множеств комплексных чисел Неравенства с двумя переменными
Неравенства с двумя переменными ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции
ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Метод Ньютона
Метод Ньютона Двоичная арифметика
Двоичная арифметика Комплексные числа
Комплексные числа Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Понятие функции
Понятие функции Тождественные преобразования алгебраических выражений (часть 1)
Тождественные преобразования алгебраических выражений (часть 1) Округление чисел
Округление чисел Классификация оптимизационных задач
Классификация оптимизационных задач 797329 (1)
797329 (1) Признаки равенства треугольников
Признаки равенства треугольников Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Плазма крови, белковый состав плазмы. Группы крови – системы АВ0 и Rh- фактор
Плазма крови, белковый состав плазмы. Группы крови – системы АВ0 и Rh- фактор Свойства логарифмов
Свойства логарифмов Деление плоскости на 9 частей
Деление плоскости на 9 частей Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ  Определители матриц
Определители матриц Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс)  Математика в профессии геодезиста
Математика в профессии геодезиста Гистограммы. Представление статистических данных в графическом виде
Гистограммы. Представление статистических данных в графическом виде Презентация на тему Формы и методы подготовки к ЕГЭ на уроках математики
Презентация на тему Формы и методы подготовки к ЕГЭ на уроках математики  Определители второго и третьего порядка. 11 класс
Определители второго и третьего порядка. 11 класс Координатный луч
Координатный луч Примеры решение задач на обработку массивов (одно- и двухмерных) на VBA
Примеры решение задач на обработку массивов (одно- и двухмерных) на VBA