2.3. Векторная алгебра

Очевидно
или
Числа называются направляющими косинусами вектора
Так как
то
т.е.

Замечание.
Если
то
При этом

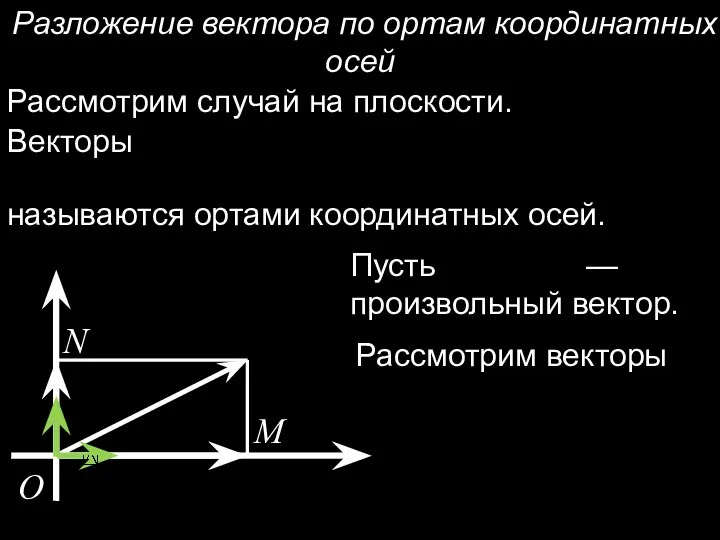
Разложение вектора по ортам координатных осей
Рассмотрим случай на плоскости.
Векторы
называются ортами координатных осей.
Пусть — произвольный вектор.
O
Рассмотрим векторы
M
N

Очевидно
Так как
то
— формула разложения вектора по ортам координатных осей.
Замечание.
Запись
равносильна записи

Замечание.
В пространстве ортами координатных осей являются векторы
Формула разложения вектора по ортам координатных осей примет вид
Пример. Найти направляющие косинусы вектора
Решение.

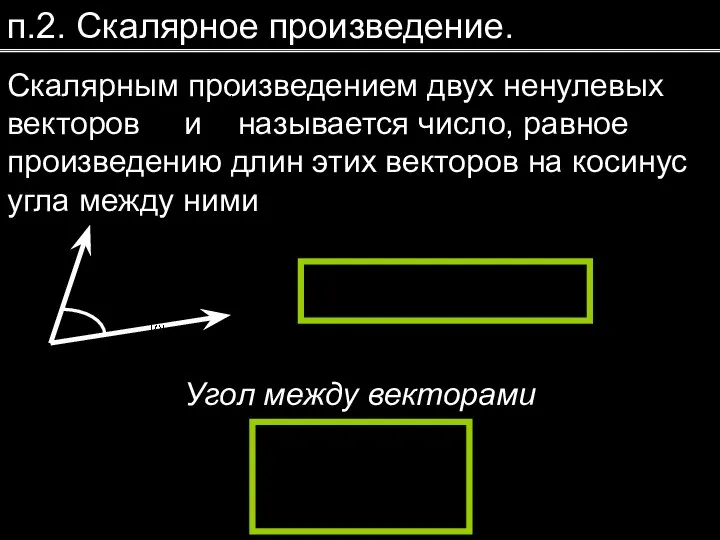
п.2. Скалярное произведение.
Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними
Угол между векторами

Свойства скалярного произведения
1)
2)
Доказательство.
Пусть
Тогда углы между векторами и равны,
Пусть
Тогда углы между векторами и являются смежными,

3)
4)
Доказательство.
Векторы называются ортогональными, если угол между ними равен 900.
5) (критерий ортогональности).
Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
Доказательство. Пусть т.е.
Если то

Выражение скалярного произведения через координаты векторов
Замечание.
Пусть
Тогда

Пример. Найти угол между векторами
Решение.

п.3. Векторное произведение.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

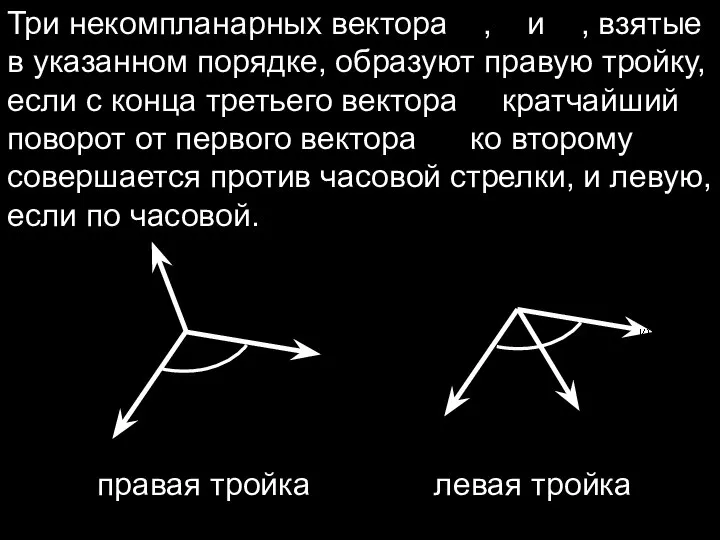
Три некомпланарных вектора , и , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора ко второму совершается против часовой стрелки, и левую, если по часовой.
правая тройка
левая тройка

Векторным произведением вектора на вектор называется вектор , удовлетворяющий условиям:
1)
2)
3)
— правая тройка.
Обозначается:

Свойства векторного произведения
1)
Доказательство.
Так как
— правая тройка,
— левая тройка,
то
противоположно направлены.
Значит,

2)
3)
Доказательство самостоятельно.
4)

Выражение векторного произведения через координаты векторов
Замечание.

Пусть
Тогда

Поэтому

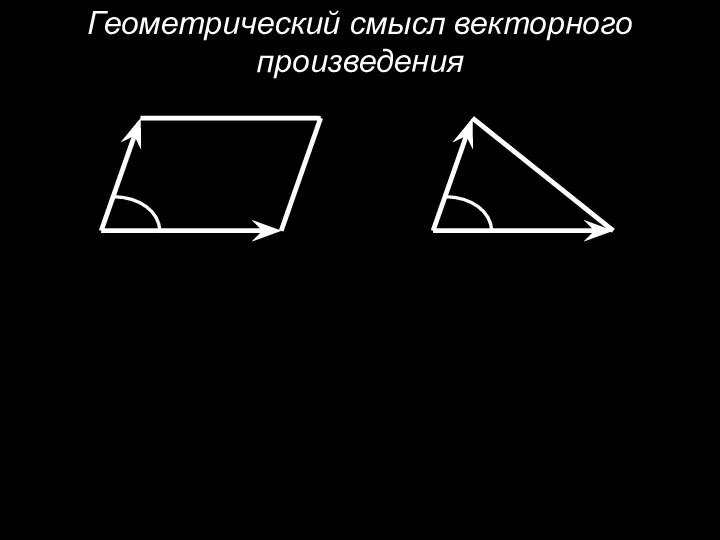
Геометрический смысл векторного произведения

п.4. Смешанное произведение.
Смешанным произведением векторов , и , взятых в указанном порядке называется скалярное произведение векторного произведения первых двух векторов и на третий вектор .
Обозначается:
Таким образом

Свойства смешанного произведения
1)
2)
3)
4)

Выражение смешанного произведения через координаты векторов
Пусть
Тогда

Поэтому

Приложения смешанного произведения
1) Если
то
— правая тройка;
— левая тройка.
если
то

2)
Пусть
тогда