Содержание
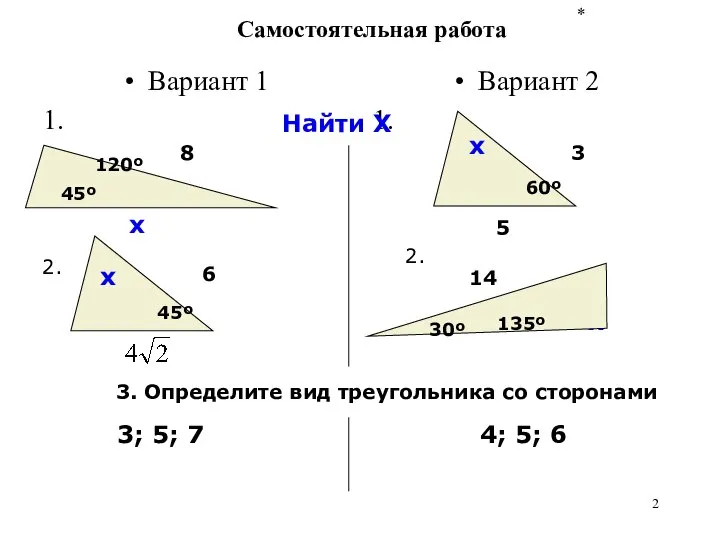
- 2. * Самостоятельная работа Вариант 1 1. Вариант 2 1. 45º 120º х 8 60º 3 х
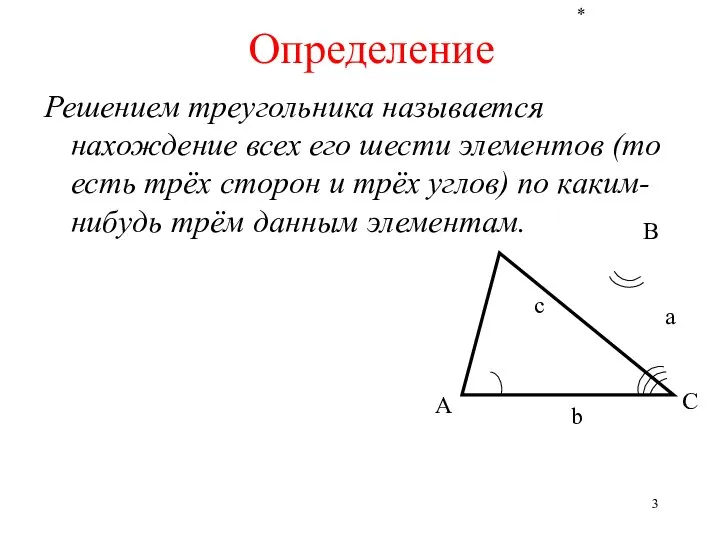
- 3. * Определение Решением треугольника называется нахождение всех его шести элементов (то есть трёх сторон и трёх
- 4. * Для этого вспомним Решение данных задач основано на использовании теорем синусов и косинусов, теоремы о
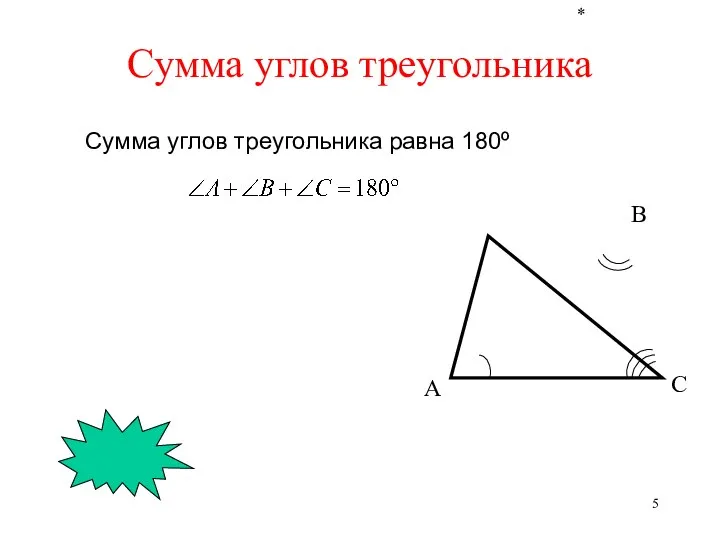
- 5. * А В С Сумма углов треугольника Сумма углов треугольника равна 180º
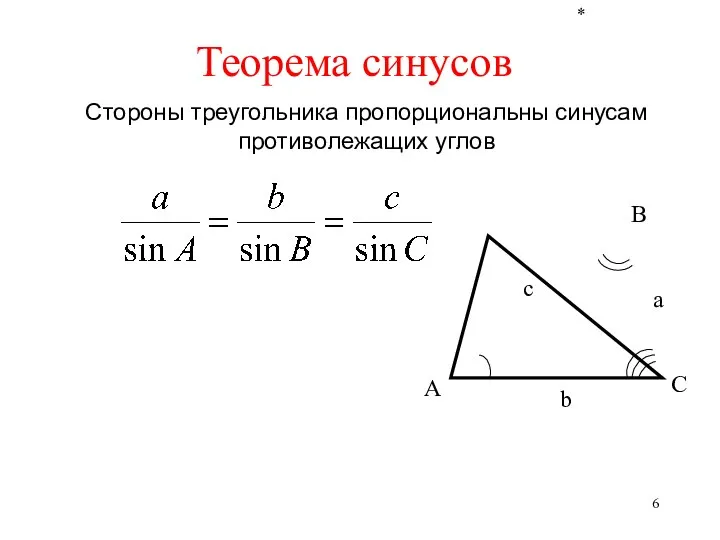
- 6. * Стороны треугольника пропорциональны синусам противолежащих углов Теорема синусов
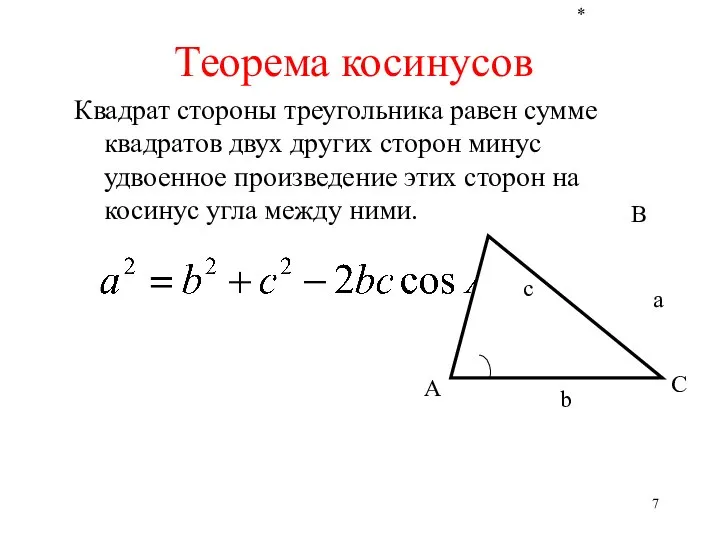
- 7. * Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на
- 8. * Три задачи на решение треугольника
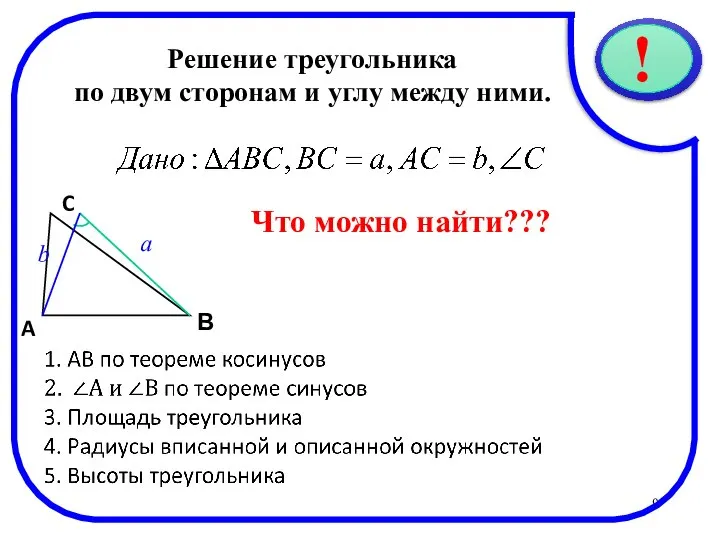
- 9. * Решение треугольника по двум сторонам и углу между ними. C В A a b Что
- 10. * Решение 2) Если γ- тупой угол, значит α и β острые углы Если γ –острый
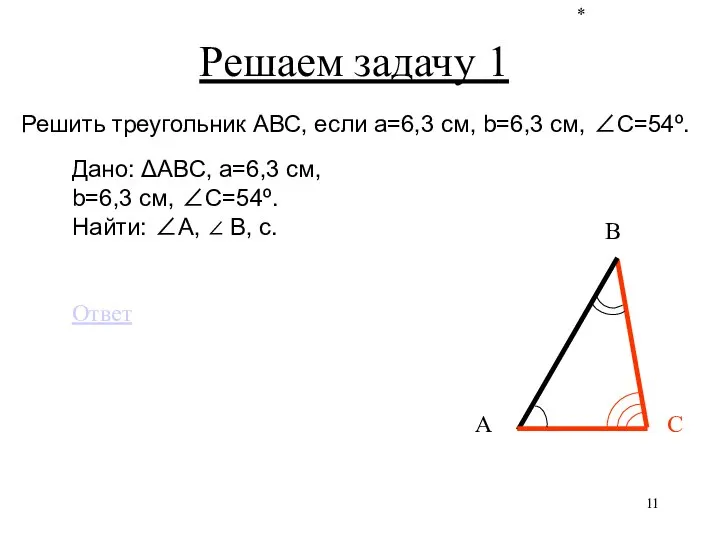
- 11. * Решаем задачу 1 С В А Решить треугольник АВС, если a=6,3 см, b=6,3 см, ∠C=54º.
- 12. * Решение треугольника по стороне и двум прилегающим к ней углам. C В A a Что
- 13. * Решение: γ = 180º - (α+β), α+β Задача имеет одно решение
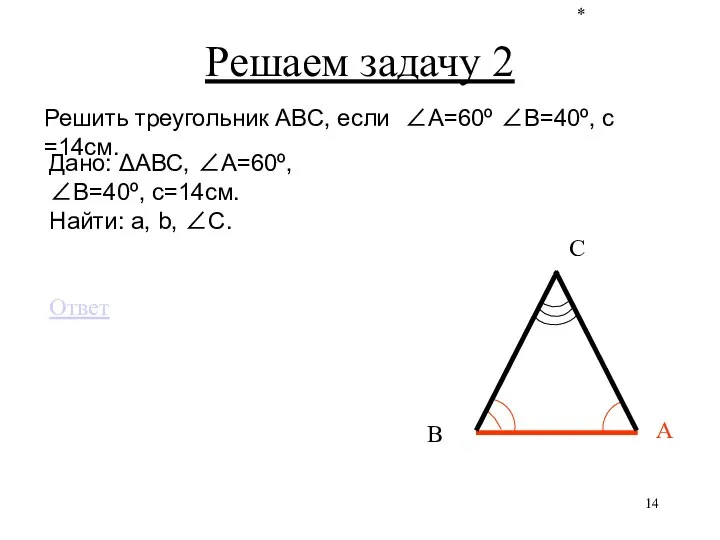
- 14. * С В А Решаем задачу 2 Решить треугольник АВС, если ∠А=60º ∠В=40º, с =14см. Дано:
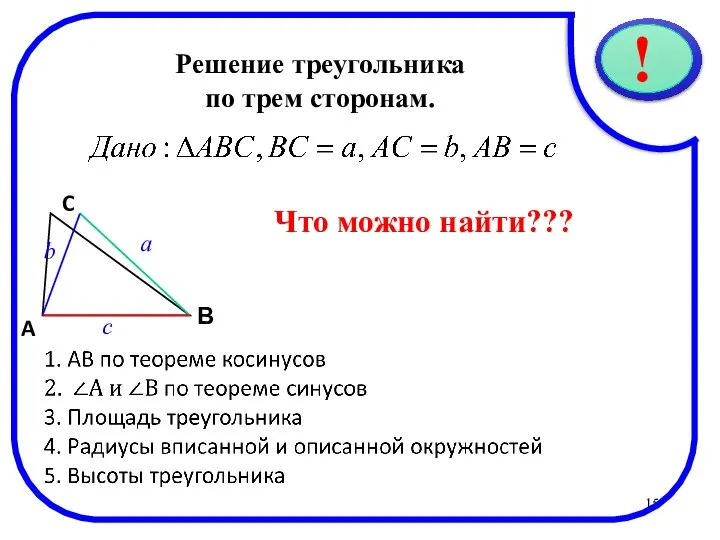
- 15. * Решение треугольника по трем сторонам. C В A a Что можно найти??? b c
- 16. * Решение Пусть а – наибольшая сторона треугольника, Задача имеет одно решение
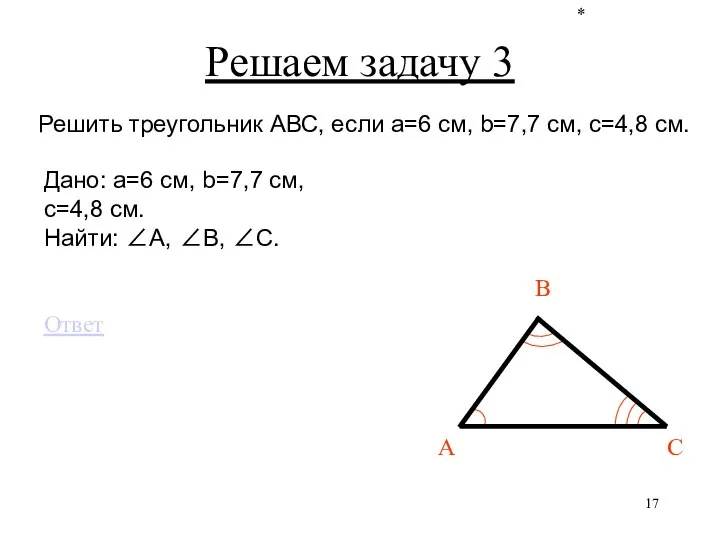
- 17. * Дано: a=6 см, b=7,7 см, c=4,8 см. Найти: ∠А, ∠B, ∠C. Ответ Решаем задачу 3
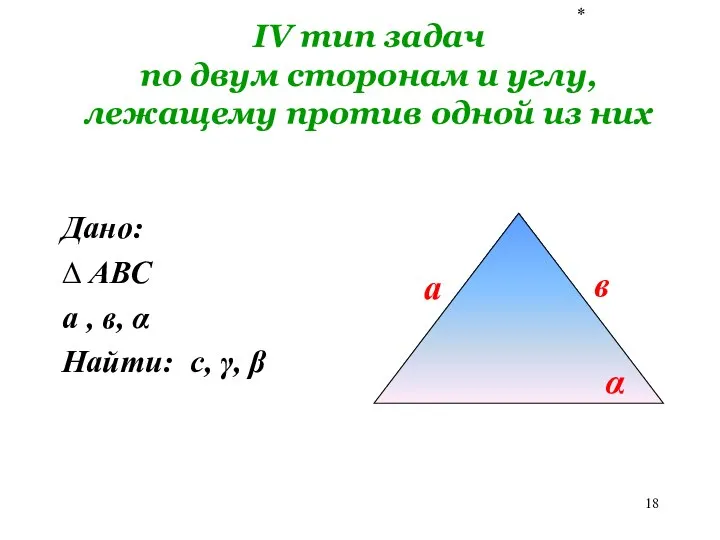
- 18. * IV тип задач по двум сторонам и углу, лежащему против одной из них Дано: ∆
- 19. * Решение 1. Если в намного больше а, то sinβ >1 и задача не имеет решений.
- 20. * 3. Если 0 Сравниваем а и в Если а существуют два угла β -острый, значит
- 21. * Таблица – памятка А С a b В А С γ a β В А
- 22. * Ответ к примеру 1 ∠А=63º ∠B=63º c≈5,7 см
- 23. * Ответ к примеру 2 ∠C=80º a≈12,3 см b≈9,1 см
- 24. * Ответ к примеру 3 ∠А=54º52´ ∠B=84º16´ ∠C=40º52´
- 25. * Найди ошибку
- 27. Скачать презентацию













 Осевая симметрия
Осевая симметрия Разминка для мозгов. Раунд 1
Разминка для мозгов. Раунд 1 Решение иррациональных уравнений. Разные методы
Решение иррациональных уравнений. Разные методы Основные правила построения сечений
Основные правила построения сечений Точка. Кривая линия. Прямая линия. Отрезок
Точка. Кривая линия. Прямая линия. Отрезок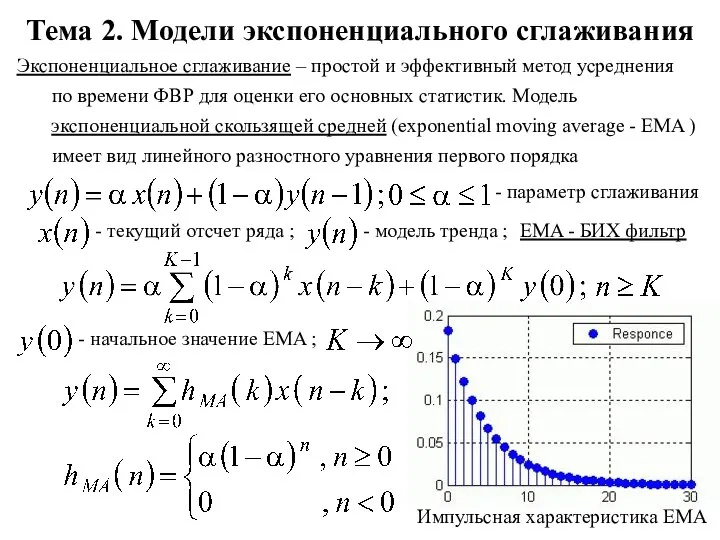 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2 Статистика знает всё
Статистика знает всё Числа и их свойства. Числовые множества. Признаки делимости
Числа и их свойства. Числовые множества. Признаки делимости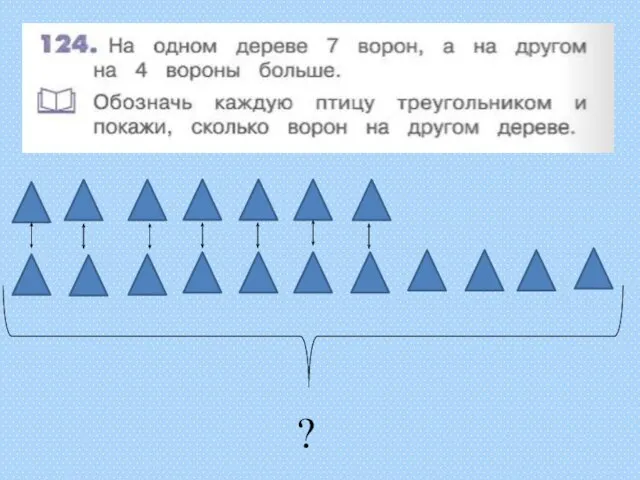 Треугольники, задача
Треугольники, задача Комбинаторика
Комбинаторика Прием письменного вычитания в случаях вида 50-24. Урок математики во 2 классе. (По УМК «Начальная школа XXI век.»)
Прием письменного вычитания в случаях вида 50-24. Урок математики во 2 классе. (По УМК «Начальная школа XXI век.») Эйлеровы графы. Лекция 08
Эйлеровы графы. Лекция 08 Обратные задачи
Обратные задачи Квадратные уравнения
Квадратные уравнения Основные геометрические фигуры
Основные геометрические фигуры Программа внеурочной деятельности Занимательная математика
Программа внеурочной деятельности Занимательная математика Діяльнісний підхід до навчання математики: сучасно та ефективно
Діяльнісний підхід до навчання математики: сучасно та ефективно Многочлен и его стандартный вид
Многочлен и его стандартный вид Пример проектной работы. Зимние олимпийские игры. Общая статистика
Пример проектной работы. Зимние олимпийские игры. Общая статистика Ребуси Вавіліної Анастасії
Ребуси Вавіліної Анастасії Умножение числа на 1
Умножение числа на 1 Построение сечений тетраэдра
Построение сечений тетраэдра Презентация на тему Линейная функция и ее график (7 класс)
Презентация на тему Линейная функция и ее график (7 класс)  1_урок_Повторение_Четырехугольники_Площадь
1_урок_Повторение_Четырехугольники_Площадь Методическая разработка по математике. Тема: Треугольники
Методическая разработка по математике. Тема: Треугольники Числовые функции
Числовые функции Угол между плоскостями
Угол между плоскостями Презентация на тему КВН по математике
Презентация на тему КВН по математике