Классическое определение вероятности

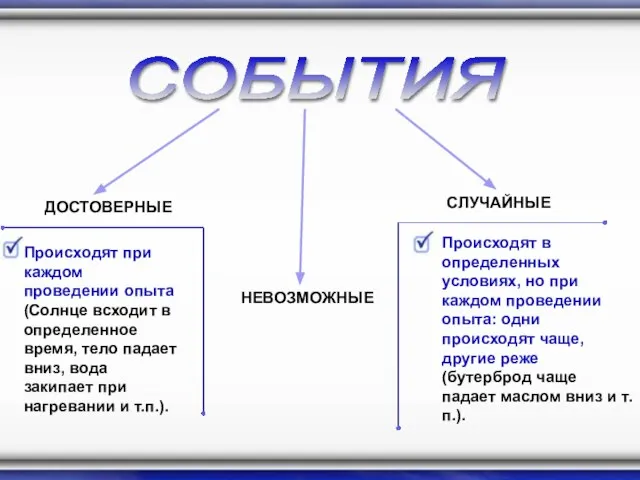
СОБЫТИЯ
ДОСТОВЕРНЫЕ
СЛУЧАЙНЫЕ
Происходят при каждом проведении опыта (Солнце всходит в определенное время, тело падает вниз, вода закипает при нагревании и т.п.).
Происходят в определенных условиях, но при каждом проведении опыта: одни происходят чаще, другие реже (бутерброд чаще падает маслом вниз и т.п.).
НЕВОЗМОЖНЫЕ

В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:
«Вероятность – возможность исполнения, осуществимости чего-нибудь».
Основатель современной теории вероятностей А.Н.Колмогоров:
«Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».

Известно, по крайней мере, шесть основных схем определения и понимания вероятности. Не все они в равной мере используются на практике и в теории, но, тем не менее, все они имеют за собой разработанную логическую базу и имеют право на существование.
Понятие вероятности

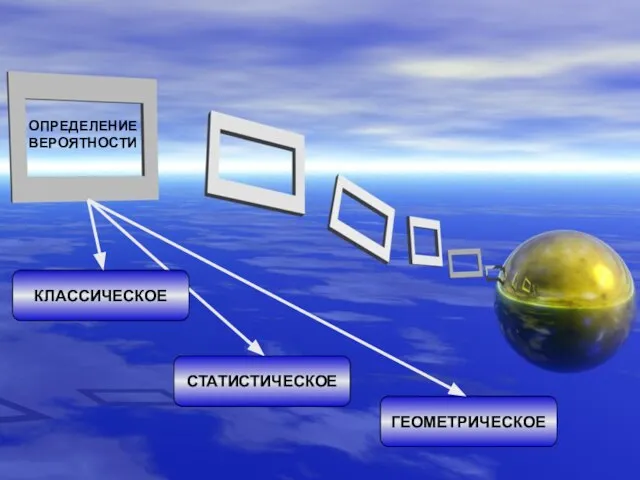
КЛАССИЧЕСКОЕ
СТАТИСТИЧЕСКОЕ
ГЕОМЕТРИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

ВЕРОЯТНОСТЬ
– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ ВЕРОЯТНОСТИ СОБЫТИЯ:
А – некоторое событие,
m – количество исходов, при которых событие А появляется,
n – конечное число равновозможных исходов.
P – обозначение происходит от первой буквы французского слова probabilite – вероятность.

Вероятностью Р наступления случайного события А называется отношение , где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.

Пьер-Симо́н Лапла́с
Классическое определение вероятности было впервые дано в работах французского математика Лапласа.

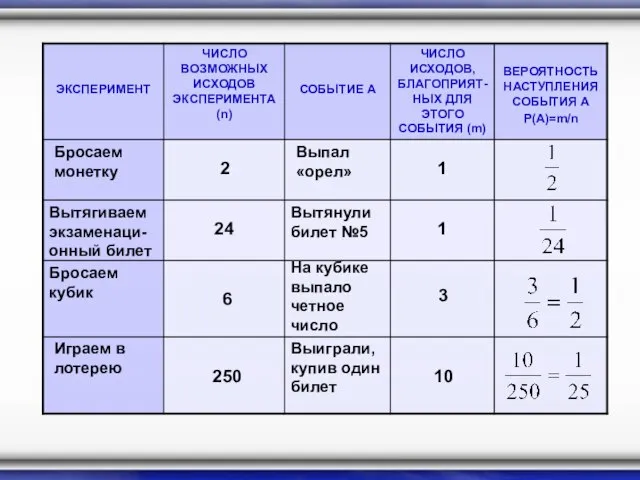
Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем кубик
На кубике выпало четное число
6
3
Играем в лотерею
Выиграли, купив один билет
250
10

Пример 1
В школе 1300 человек, из них 5 человек хулиганы.
Какова вероятность того, что один из них попадётся директору на глаза?

Вероятность:
P(A) = 5/1300 = 1/250.
Решение

Пример 2.
При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих кубиках выпадут одинаковые числа?

Решение
Составим следующую таблицу
Вероятность: P(A)=6/36= =1/6.

Пример 3.
Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятные?
с
т
а
т
и
с
т
и
к
а

Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) = 2/10 = 1/5;
буква «т» встречается 3 раза –
P(т) = 3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.
Решение

Свойства вероятности

Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события А не меньше , но не больше
?
1
?
?
?
0
1
0

P(u) = 1 (u – достоверное событие);
P(v) = 0 (v – невозможное событие);
0 ≤ P(A) ≤ 1.

Самостоятельная
работа

Задача 1.
В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.

а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:
P=3:9=1/3=0,33(3)
б) Мы имеем всевозможных случаев 9. Благоприятствующих событий 2. Вероятность равна P=2:9=0,2(2)
в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)
Решение

Задача 2.
В коробке лежат 10 одинаковых шаров, на каждом из которых написан его номер от 1 до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3.

Всевозможных событий 6 (красный №1 - красный №2; красный №1 - белый; красный №2 - белый; красный №3 - красный №2; красный №3 - красный №1; красный №3 - белый) из них благоприятных 3. Выигрывает тот, кто вытаскивает 2 красных шара.
Решение

Задача 3.
Мальчики играли в “Орлянку”. Но монетка куда-то закатилась. Предложите, как заменить ее игральным кубиком?

Считать "орел" - четное число, а "решка" - не четное число.
Решение

Задача 4.
Какую справедливую игру можно предложить двум девочкам, у которых есть 3 красных и 1 белый шарик и мешок?

Всевозможных событий 6 (красный №1 - красный №2; красный №1 - белый; красный №2 - белый; красный №3 - красный №2; красный №3 - красный №1; красный №3 - белый) из них благоприятных 3. Выигрывает тот, кто вытаскивает 2 красных шара.
Решение

Задача 5.
В настольной игре сломалась вертушка с тремя разными секторами: красным, белым и синим, но есть кубик. Как заменить вертушку?