Содержание
- 2. Содержание. Вводная часть, повторение теоретического материала. Решение тригонометрических уравнений. Проблемы, возникающие при решении тригонометрических уравнений.
- 3. ЦЕЛЬ: Повторить решение тригонометрических уравнений. 1. Знать формулы для решения простейших тригонометрических уравнений. 2. Различать типы
- 4. Устная работа. Решите уравнения А) 3 х – 5 = 7 Б) х2 – 8 х
- 5. Устная работа Упростите выражения А) (sin a – 1) (sin a + 1) Б) sin2 a
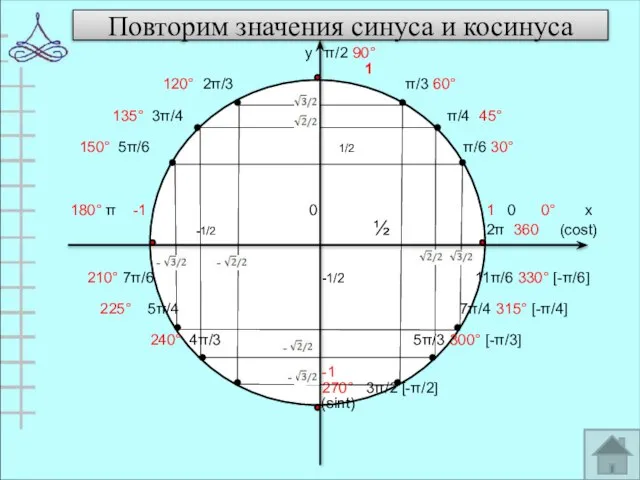
- 6. Повторим значения синуса и косинуса у π/2 90° 1 120° 2π/3 π/3 60° 135° 3π/4 π/4
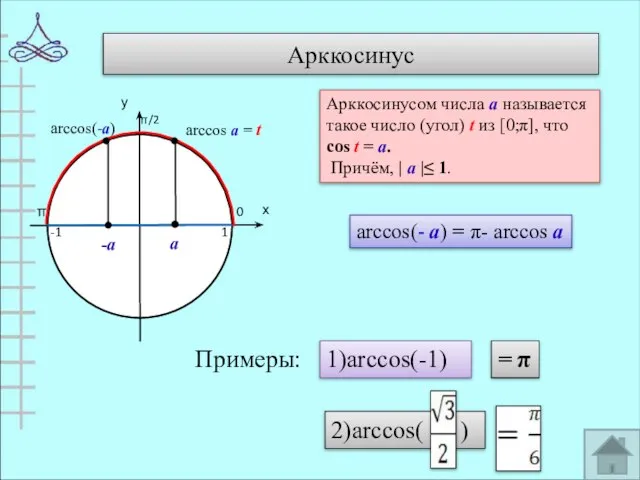
- 7. Арккосинус 0 π 1 -1 arccos(-а) Арккосинусом числа а называется такое число (угол) t из [0;π],
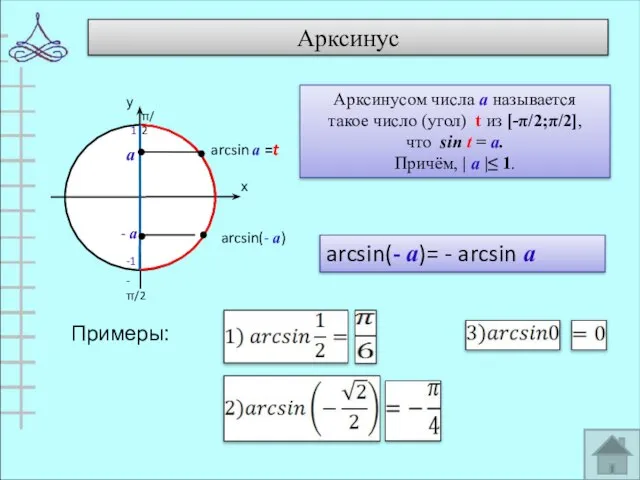
- 8. Арксинус Примеры: а - а arcsin(- а)= - arcsin а Арксинусом числа а называется такое число
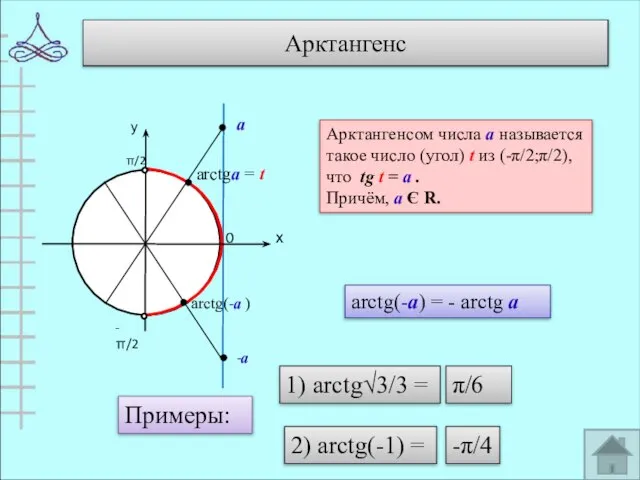
- 9. Арктангенс 0 arctgа = t Арктангенсом числа а называется такое число (угол) t из (-π/2;π/2), что
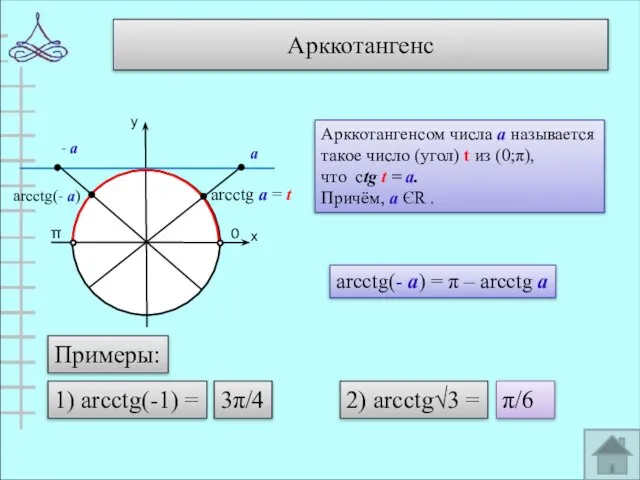
- 10. Арккотангенс у х 0 π arcctg а = t Арккотангенсом числа а называется такое число (угол)
- 11. Повторение 1 вариант sin (-π/3) cos 2π/3 tg π/6 ctg π/4 cos (-π/6) sin 3π/4 arcsin
- 12. Повторение Ответы 1 вариант - √3/2 - 1/2 √3/3 1 √3/2 √2/2 π/4 0 - π/6
- 13. Формулы корней простейших тригонометрических уравнений 1.cost = а , где |а| ≤ 1 или Частные случаи
- 14. Формулы корней простейших тригонометрических уравнений 2. sint = а, где | а |≤ 1 или Частные
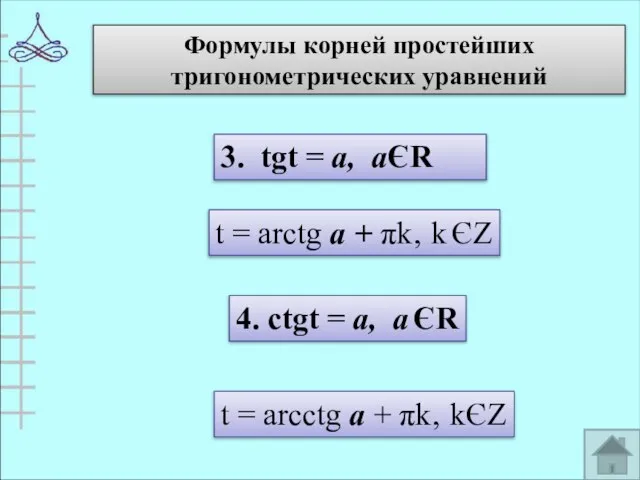
- 15. Формулы корней простейших тригонометрических уравнений 3. tgt = а, аЄR t = arctg а + πk‚
- 16. При каких значениях х имеет смысл выражение: 1.arcsin(2x+1) 2.arccos(5-2x) 3.arccos(x²-1) 4.arcsin(4x²-3x) 1) -1≤ 2х+1 ≤1 -2≤
- 17. Примеры: cost= - ; 2) sint = 0; 3) tgt = 1; t= ±arccos(-1/2)+2πk, kЄZ t=
- 18. Решение простейших уравнений tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4
- 19. Виды тригонометрических уравнений 1.Сводимые к квадратным Решаются методом введения новой переменной a∙sin²x + b∙sinx + c=0
- 20. 2.Однородные 1)Первой степени: Решаются делением на cos х (или sinx) и методом введения новой переменной. a∙sinx
- 21. 2) Однородные уравнения второй степени: Решаются делением на cos² х (или sin²x) и методом введения новой
- 22. Виды тригонометрических уравнений 3. Уравнение вида: А sinx + B cosx = C. А, В, С
- 23. Виды тригонометрических уравнений 4. Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки Решаются с помощью введения
- 24. Формулы. Универсальная подстановка. х ≠ π + 2πn; Проверка обязательна! Понижение степени. = (1 + cos2x
- 25. Правила. Увидел квадрат – понижай степень. Увидел произведение – делай сумму. Увидел сумму – делай произведение.
- 26. 1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2.
- 27. Решение тригонометрических уравнений по известным алгоритмам Вариант 1. На «3» 3 sin x+ 5 cos x
- 29. Скачать презентацию




















 Формулы дифференцирования
Формулы дифференцирования Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Подготовка к ЕГЭ. Повторение. Математика
Подготовка к ЕГЭ. Повторение. Математика Сумма углов треугольника
Сумма углов треугольника Подготовка к контрольной работе по математике
Подготовка к контрольной работе по математике Длина окружности
Длина окружности Макет школи майбутнього виконаний із геометричних тіл
Макет школи майбутнього виконаний із геометричних тіл Презентация на тему Алгоритм решения задач на пропорции
Презентация на тему Алгоритм решения задач на пропорции  Путешествие в страну Математику
Путешествие в страну Математику Гра в нормальній формі. Формалізований вид гри
Гра в нормальній формі. Формалізований вид гри Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов
Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов Четные и нечётные функции
Четные и нечётные функции Развитие понятия о числе
Развитие понятия о числе Прибавить и вычесть число 3. Решение текстовых задач
Прибавить и вычесть число 3. Решение текстовых задач Разработка метода управления адаптивной системой защитного видеонаблюдения на основе контроля динамики изменения кадра
Разработка метода управления адаптивной системой защитного видеонаблюдения на основе контроля динамики изменения кадра Разложение на множители способом группировки
Разложение на множители способом группировки Теорема Пифагора
Теорема Пифагора Неопределенный интеграл. Лекция 2.1
Неопределенный интеграл. Лекция 2.1 Иррациональные неравенства
Иррациональные неравенства Методичні основи вивчення властивостей арифметичних дій
Методичні основи вивчення властивостей арифметичних дій Уравнение Бернулли
Уравнение Бернулли Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей
Роль дисплазии соединительной ткани в формировании остеопенического синдрома у детей Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Односторонние пределы
Односторонние пределы Математический экспресс. Городской конкурс юных математиков среди 6-х классов
Математический экспресс. Городской конкурс юных математиков среди 6-х классов Сложение в пределах 20
Сложение в пределах 20 Операции, функции, выражения
Операции, функции, выражения История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1