Содержание
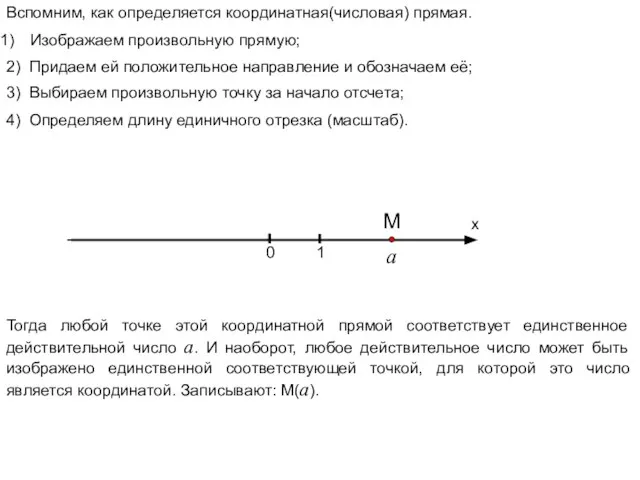
- 2. Вспомним, как определяется координатная(числовая) прямая. Изображаем произвольную прямую; х 0 1 М а Тогда любой точке
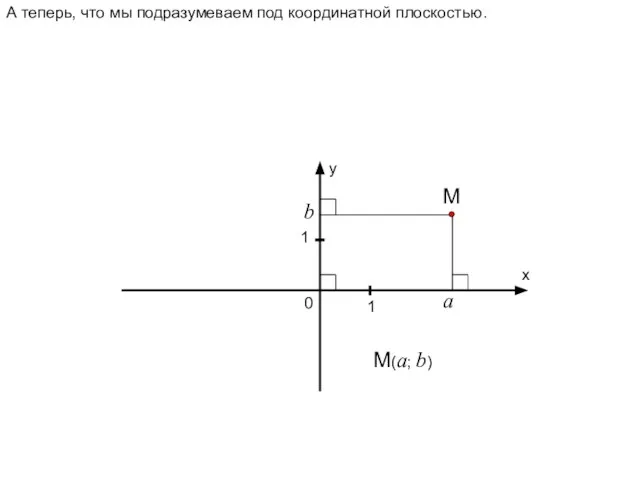
- 3. А теперь, что мы подразумеваем под координатной плоскостью. у х 0 1 1 М а b
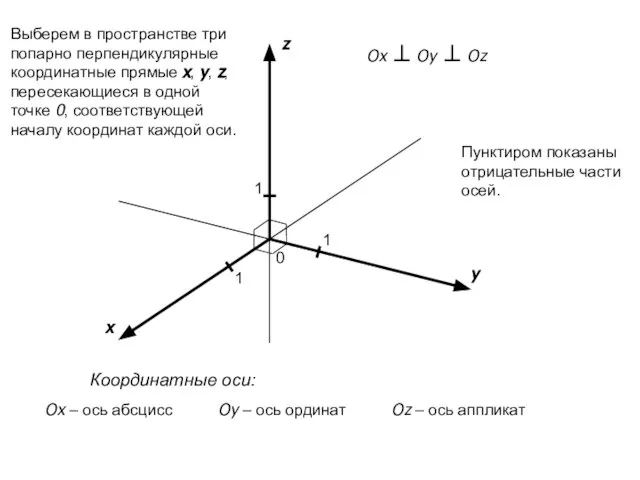
- 4. x y z 0 1 Ox ⊥ Oy ⊥ Oz Ox – ось абсцисс Oy –
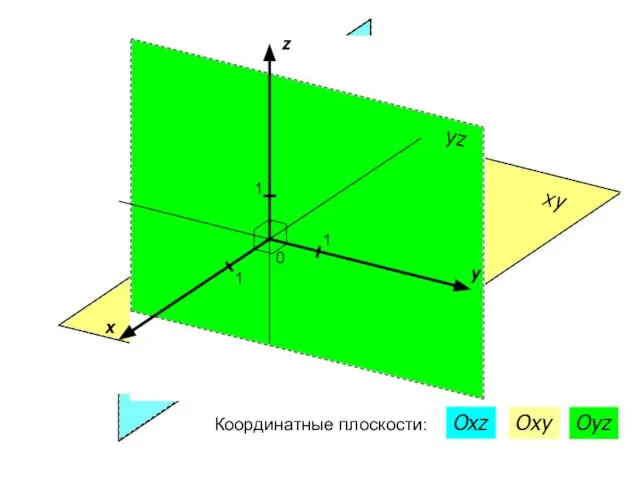
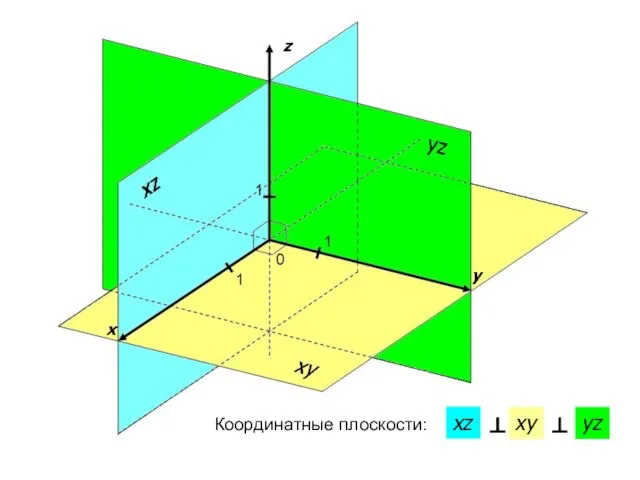
- 5. x y z 0 1 1 1 Координатные плоскости: Oxz Oxy Oyz
- 6. Координатные плоскости: xz ⊥ xy ⊥ yz
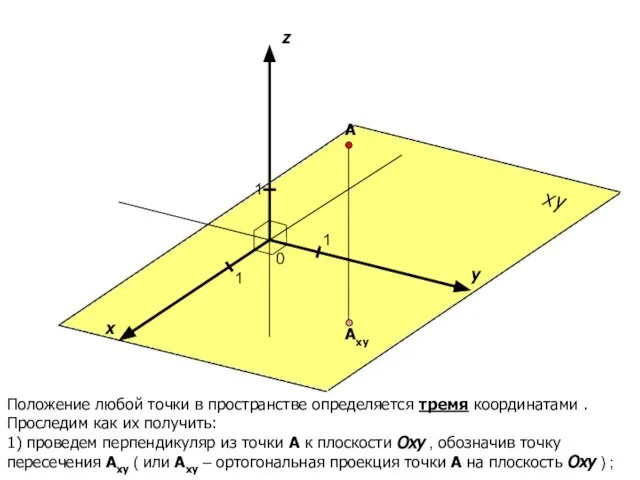
- 7. Положение любой точки в пространстве определяется тремя координатами . Проследим как их получить: 1) проведем перпендикуляр
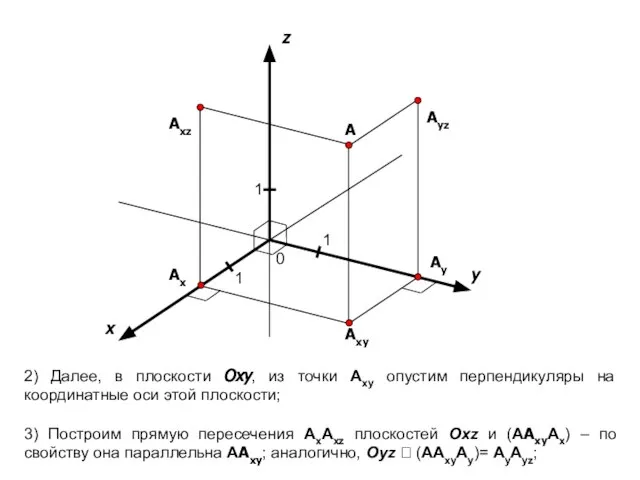
- 8. x y 1 1 A Ayz Axz Axy Ax Ay z 1 2) Далее, в плоскости
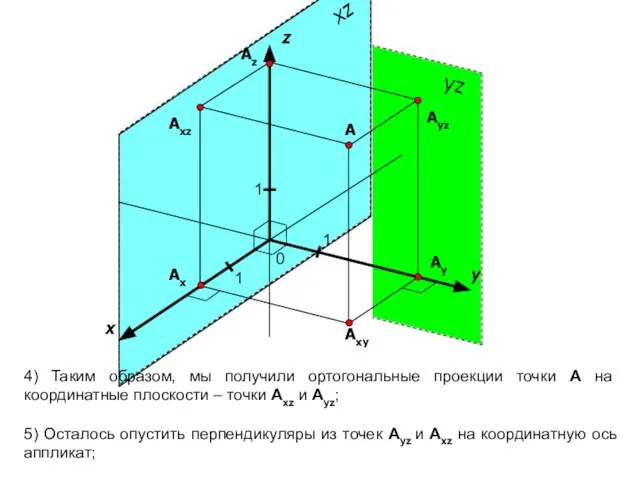
- 9. x y 1 1 A Ayz Axz Axy Ax Ay z 1 4) Таким образом, мы
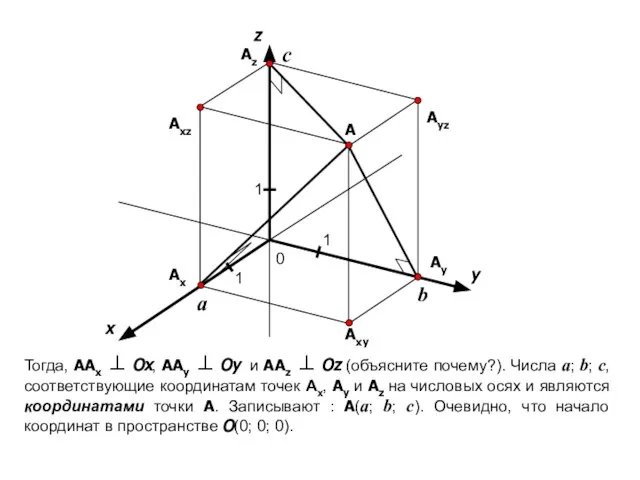
- 10. x y 0 1 1 1 A Ayz Axz Axy Ax Az Ay z Тогда, AAx
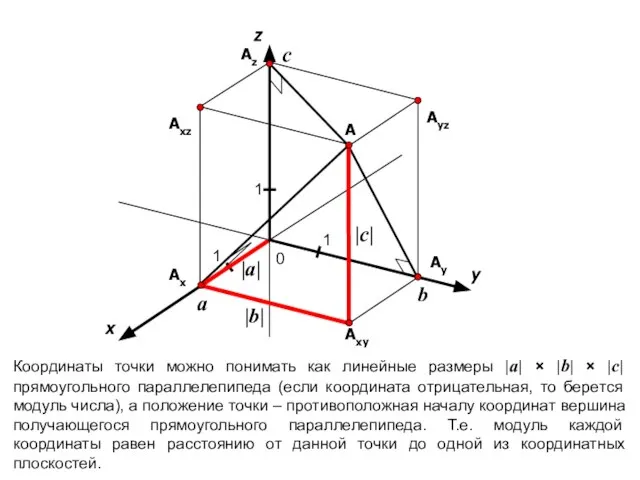
- 11. x y 0 1 1 1 A Ayz Axz Axy Ax Az Ay z Координаты точки
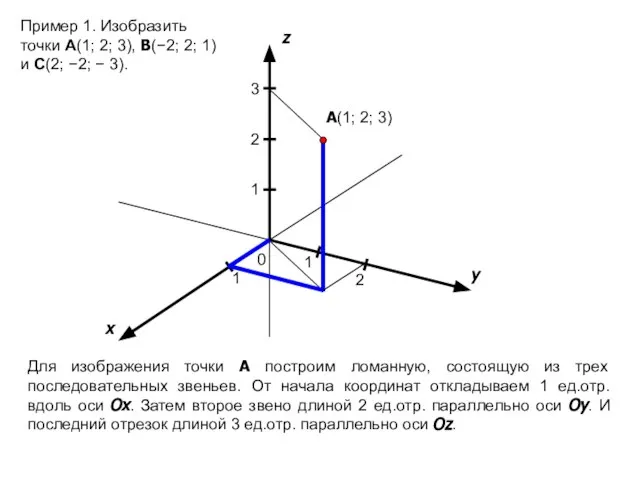
- 12. 1 x y z 0 1 1 2 3 2 Пример 1. Изобразить точки A(1; 2;
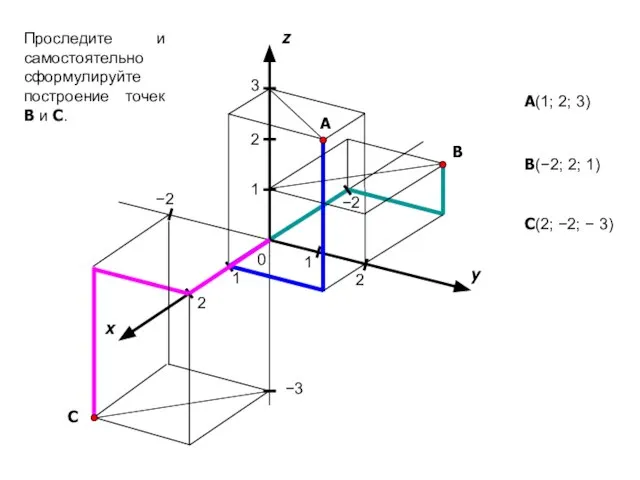
- 13. x y z 0 1 1 A 1 2 3 2 A(1; 2; 3) B −2
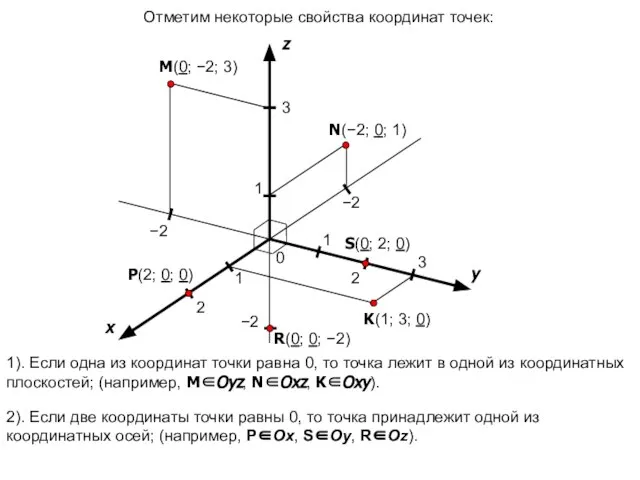
- 14. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей;
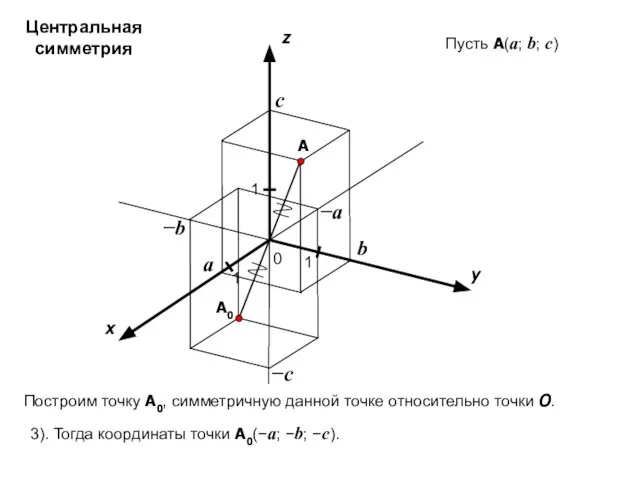
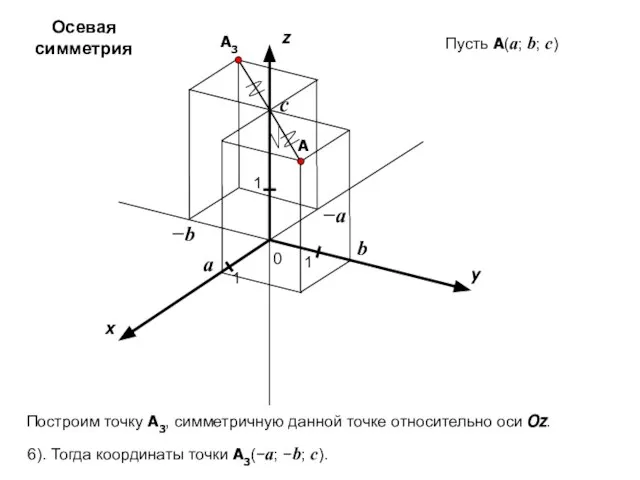
- 15. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) −a
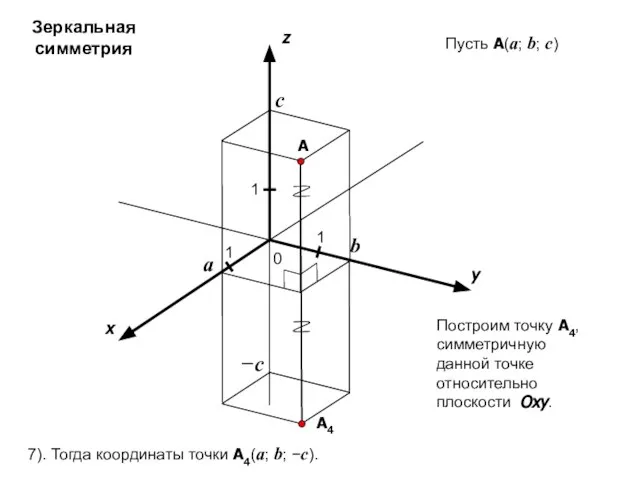
- 16. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) −c
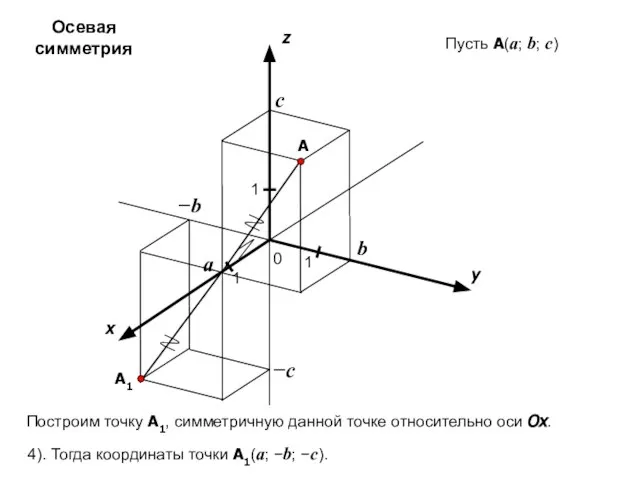
- 17. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) −c
- 18. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) −a
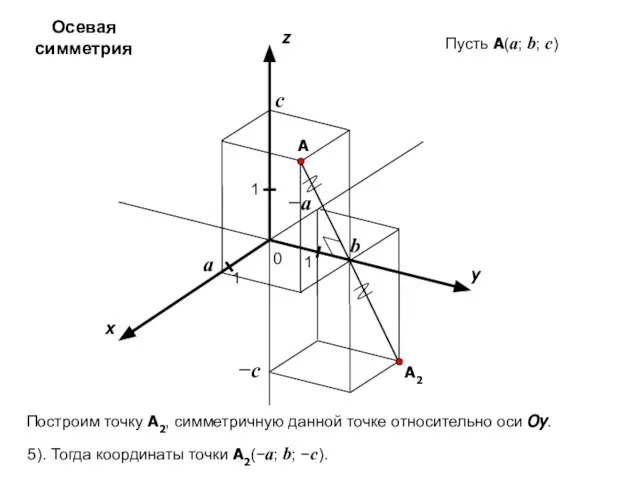
- 19. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) −c
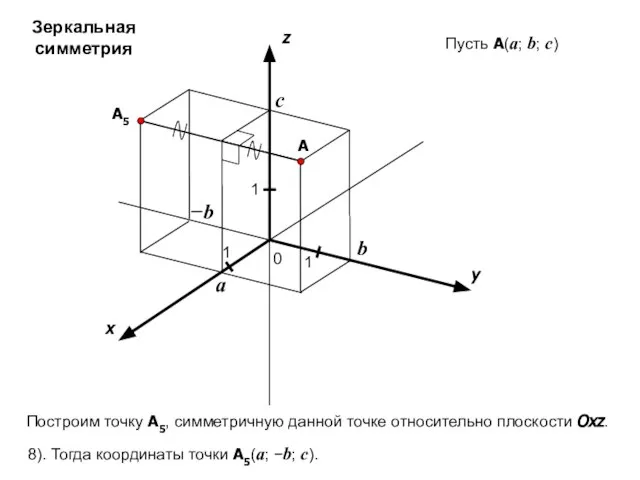
- 20. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) −b
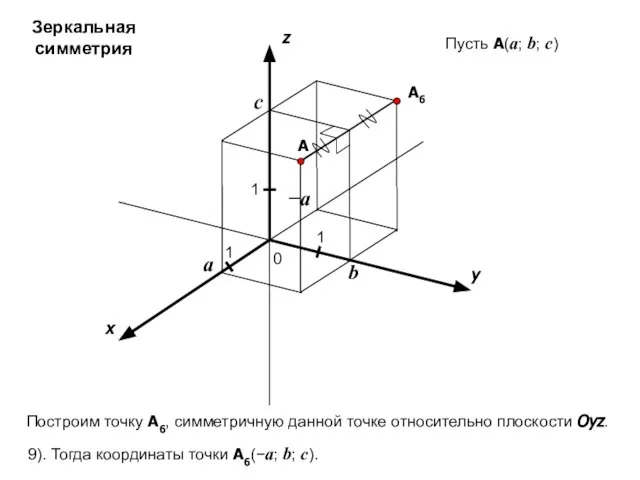
- 21. x y z 0 1 1 A 1 a b c Пусть A(a; b; c) A6
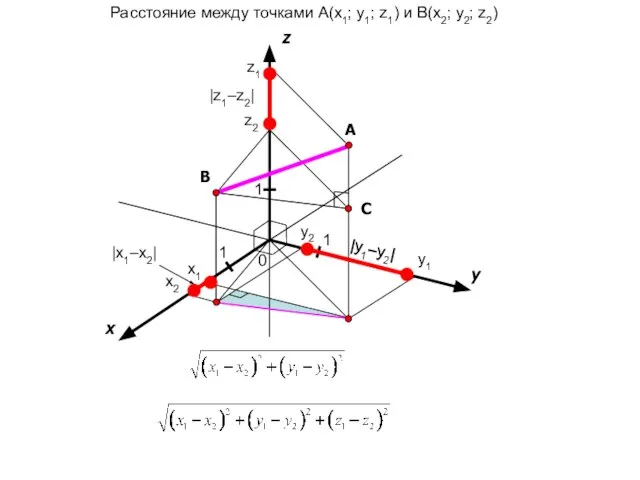
- 22. x y 0 1 1 A z 1 Расстояние между точками A(x1; y1; z1) и B(x2;
- 24. Скачать презентацию
 08_ ОТС_ Основы теории СП-2
08_ ОТС_ Основы теории СП-2 Презентация на тему ЗАДАЧИ НА ЧАСТИ
Презентация на тему ЗАДАЧИ НА ЧАСТИ  Презентация на тему Степени
Презентация на тему Степени  Тригонометрия. Подготовка к диагностической работе
Тригонометрия. Подготовка к диагностической работе Начала теории вероятности
Начала теории вероятности Линейная алгебра, теория вероятностей и математический анализ
Линейная алгебра, теория вероятностей и математический анализ История происхождения дробей
История происхождения дробей Задачи-головоломки
Задачи-головоломки Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (3)
Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (3) Деление квадрата на 4 равные части
Деление квадрата на 4 равные части 865f4a04-e6d6-4374-8401-b49cfc41ea6e
865f4a04-e6d6-4374-8401-b49cfc41ea6e Презентация на тему ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Презентация на тему ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА  Применение признаков равенства треугольников к решению задач
Применение признаков равенства треугольников к решению задач Критерий углового преобразования Фишера
Критерий углового преобразования Фишера Булева алгебра. Классы булевых функций
Булева алгебра. Классы булевых функций Способы задания арифметической прогрессии
Способы задания арифметической прогрессии Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки Осевая симметрия
Осевая симметрия Урок математики 3 класс
Урок математики 3 класс Кривые Безье
Кривые Безье Операции над графами
Операции над графами Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Задание 2 по математике
Задание 2 по математике В мире плоскостей
В мире плоскостей Решение логических задач. Математические основы информатики
Решение логических задач. Математические основы информатики Рефлексия. Задачи. Домашняя работа
Рефлексия. Задачи. Домашняя работа