Презентация по математике "Кто вьёт самые красивые гнёзда?" -

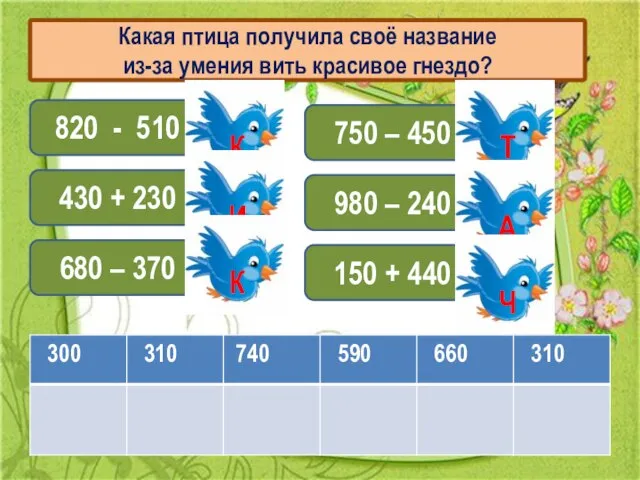
Какая птица получила своё название
из-за умения вить красивое гнездо?
820 - 510
К
430 + 230
И
680 – 370
К
750 – 450
980 – 240
150 + 440
Т
А
Ч

ТКАЧИК

Ткачики получили свое имя благодаря умению строить необычайно искусные гнезда. Некоторые выглядят как шары с боковым входом. У других овальная форма, а леток приделан сбоку. Третьи круглые, а леток выглядит как длинная трубка, ведущая вниз. Гнезда ткутся из травинок, а внутри выстилаются тонкими растительными волокнами и перьями. Они бывают подвешенными на стебельках травы или на тонких ветках кустарников или деревьев. Благодаря этому яйца и птенцы находятся в таких гнездах в безопасности. Гнезда хоть и качаются на ветру, но недоступны для змей и других хищников.

ТКАЧИК

ТКАЧИК