О точки X и Y отобразились на X' и Y'. Тогда, как ясно из определения центральной симметрии, OX' = -OX, OY' = -OY.
Вместе с тем XY = OY - OX, X'Y' = OY' - OX'
Поэтому имеем: X'Y' = -OY + OX = -XY
Отсюда выходит, что центральная симметрия является движением, изменяющим направление на противоположное и наоборот, движение, изменяющее направление на противоположное, есть центральная симметрия.
Y'
Y
X'
X
O
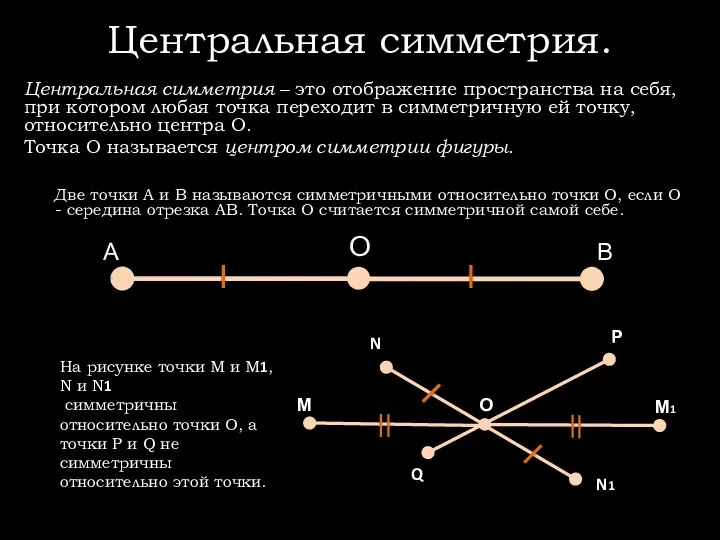
Свойство центральной симметрии: центральная симметрия переводит прямую (плоскость) в себя или в параллельную ей прямую (плоскость).



 Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  тринометрические функции
тринометрические функции Деление одночлена на одночлен
Деление одночлена на одночлен Теоремы сложения и умножения вероятностей
Теоремы сложения и умножения вероятностей Двоичная арифметика
Двоичная арифметика Презентация на тему Умножение суммы на число
Презентация на тему Умножение суммы на число  Обучение решению задач на движение при обобщающем повторении
Обучение решению задач на движение при обобщающем повторении Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Область визначення функції
Область визначення функції Презентация на тему Тренажер по формулам сокращенного умножения
Презентация на тему Тренажер по формулам сокращенного умножения  Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Таблицы, часть 1, 5-9 классы
Таблицы, часть 1, 5-9 классы Predel_funktsii_v_tochke
Predel_funktsii_v_tochke Цилиндр, конус, шар. Решение задач
Цилиндр, конус, шар. Решение задач Название круглых сотен
Название круглых сотен Треугольник и его виды
Треугольник и его виды Классическое определение вероятности
Классическое определение вероятности Множества и операции над ними
Множества и операции над ними Reshenie_zadach_1
Reshenie_zadach_1 Площадь параллелограмма
Площадь параллелограмма Десятичные дроби. Тест
Десятичные дроби. Тест Система географических координат
Система географических координат Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5
Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5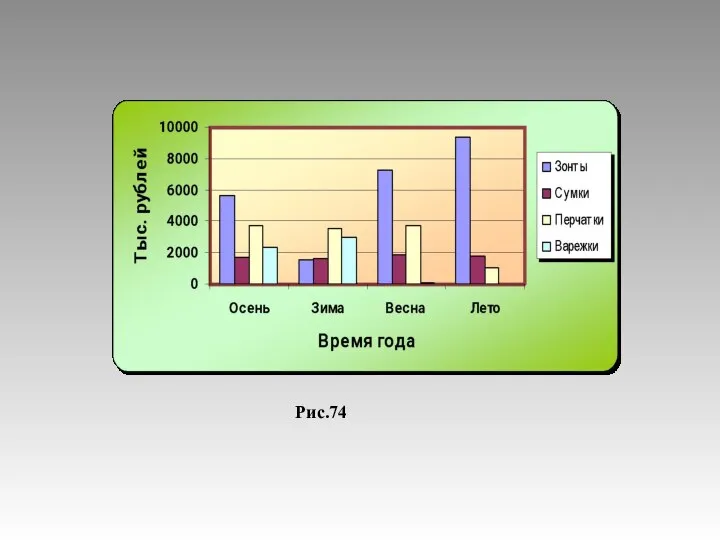 Диаграммы. Фронтальная работа. 6 класс
Диаграммы. Фронтальная работа. 6 класс неопред интеграл
неопред интеграл Презентация на тему Математический КВН
Презентация на тему Математический КВН  Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников
Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников