Содержание
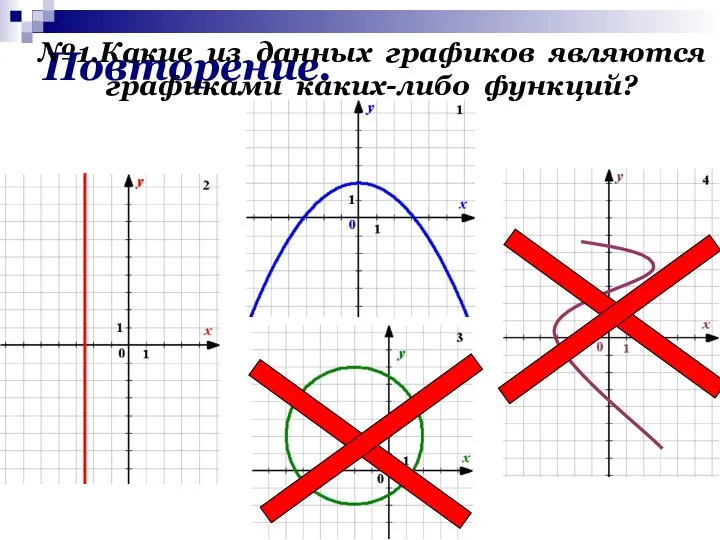
- 2. Повторение. №1.Какие из данных графиков являются графиками каких-либо функций?
- 3. № 2. Повторение. Линейные функции. y = ах + b Верно!
- 4. № 2. Повторение. Функции прямой пропорциональности. у = kx Правильно!
- 5. № 2. Повторение. Функции обратной пропорциональности. у = k/x И все!
- 6. № 2. Повторение. Квадратичные функции. Молодцы! у = ах2 + bx +c
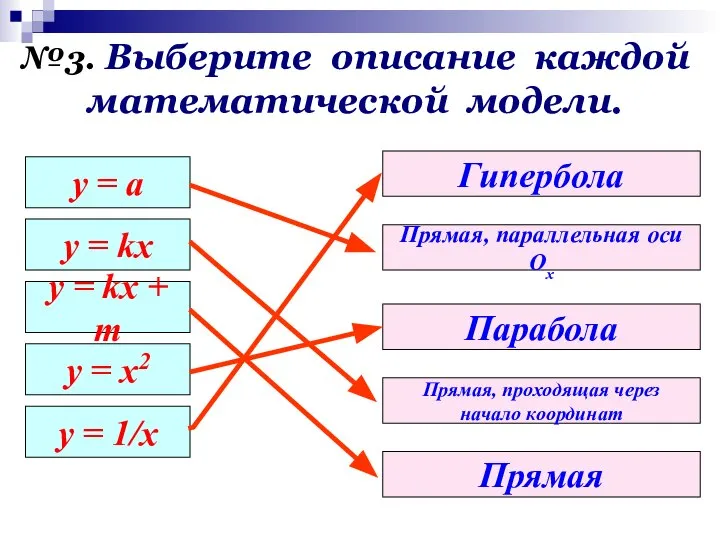
- 7. у = а y = kx y = kx + m y = x2 y =
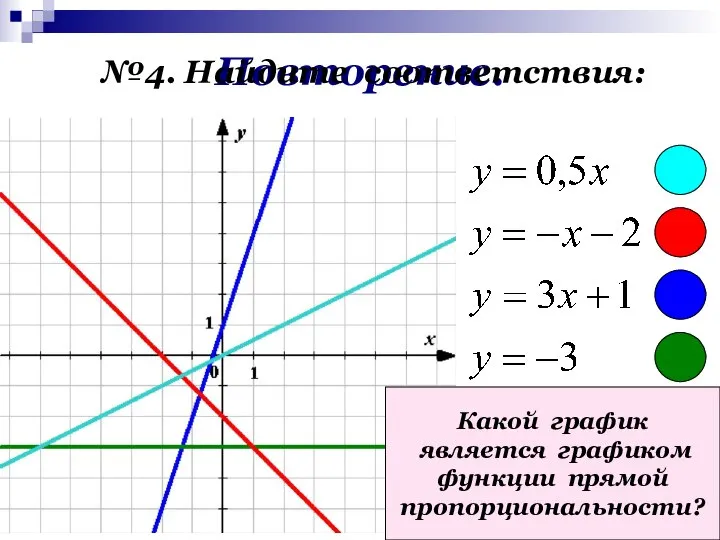
- 8. Повторение. №4. Найдите соответствия: Какой график является графиком функции прямой пропорциональности?
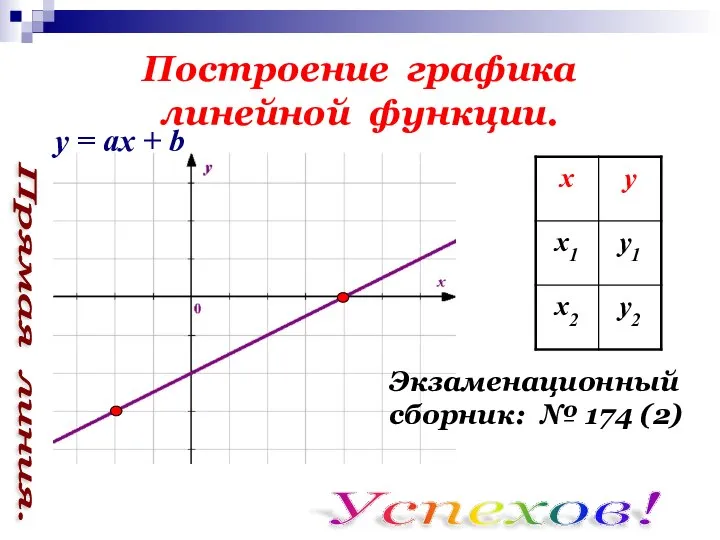
- 9. Построение графика линейной функции. Экзаменационный сборник: № 174 (2) Успехов! Прямая линия. y = ах +
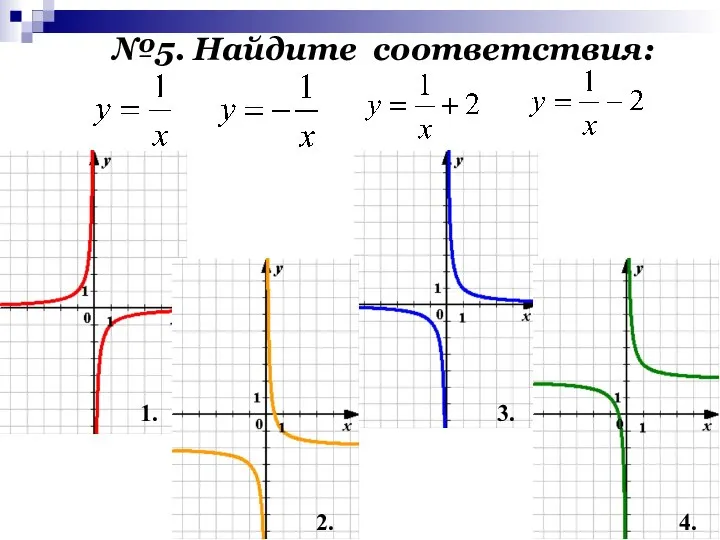
- 10. №5. Найдите соответствия: 1. 3. 2. 4.
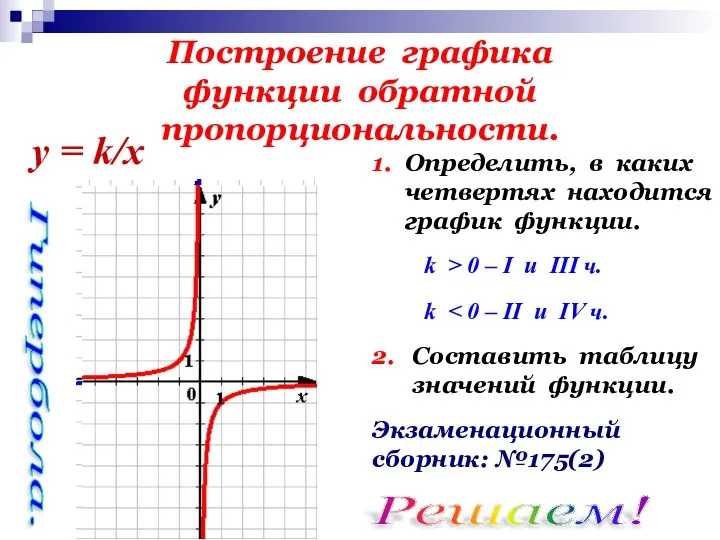
- 11. Построение графика функции обратной пропорциональности. 1. Определить, в каких четвертях находится график функции. 2. Составить таблицу
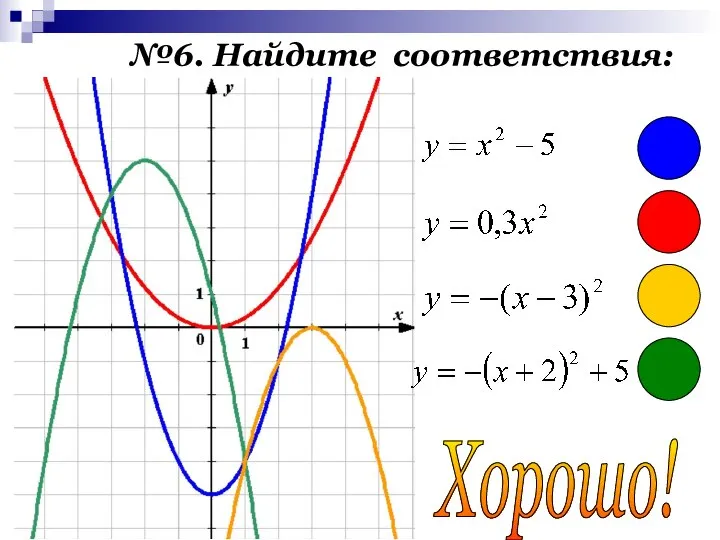
- 12. №6. Найдите соответствия: Хорошо!
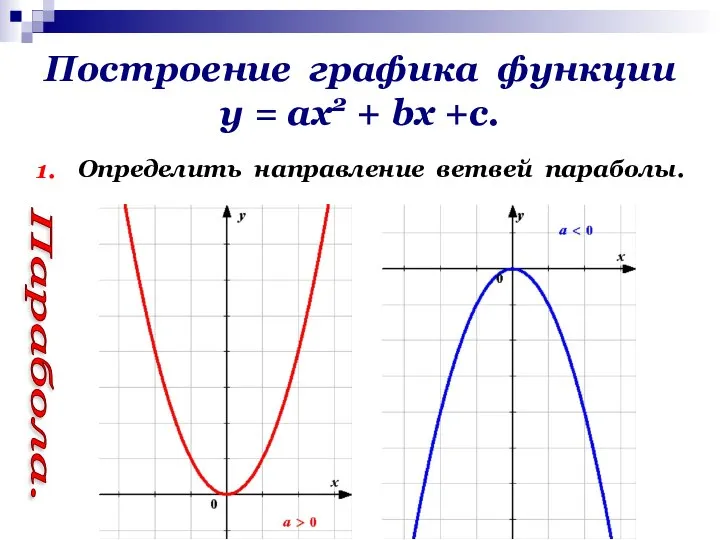
- 13. Построение графика функции у = ах2 + bх +с. 1. Определить направление ветвей параболы. Парабола.
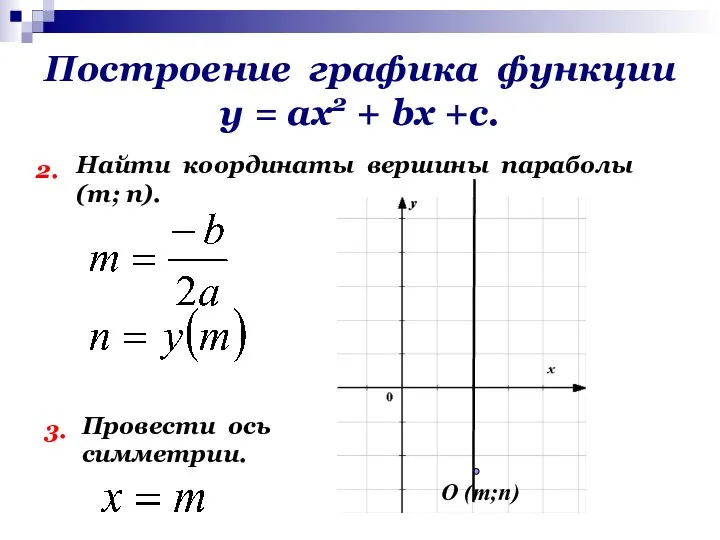
- 14. Построение графика функции у = ах2 + bх +с. 2. Найти координаты вершины параболы (т; п).
- 15. Построение графика функции у = ах2 + bх +с. 4. Определить точки пересечения графика функции с
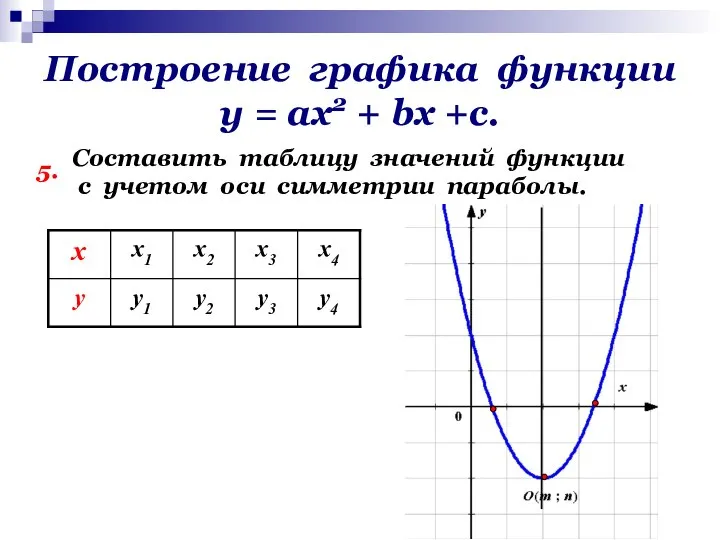
- 16. Построение графика функции у = ах2 + bх +с. 5. Составить таблицу значений функции с учетом
- 17. Алгоритм построения графика функции у = ах2 + bх +с. 1. Определить направление ветвей параболы. 2.
- 18. Домашнее задание: Учебник Алгебра -10: № 8(1-4) № 4(1,3)
- 19. 1. г Каков вид графика функции обратной пропорциональности? и е п а л о б р
- 20. 1. 2. р г и е п а л о б р Каков вид графика квадратичной
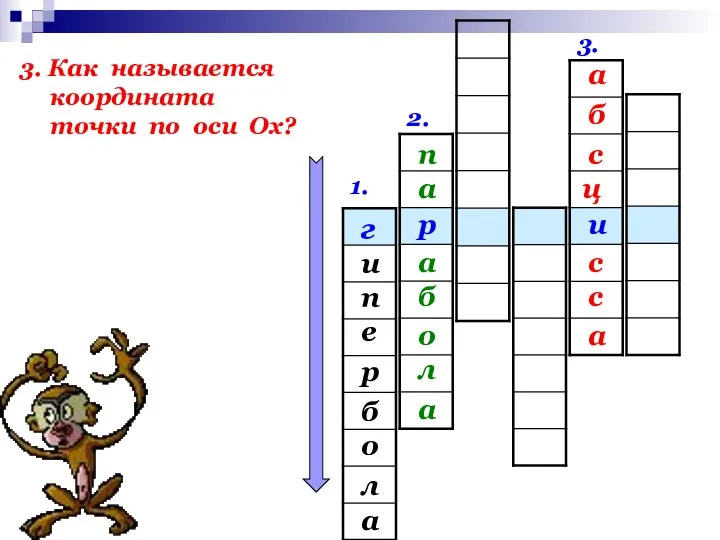
- 21. 1. 2. 3. и р г и е п а л о б р 3. Как
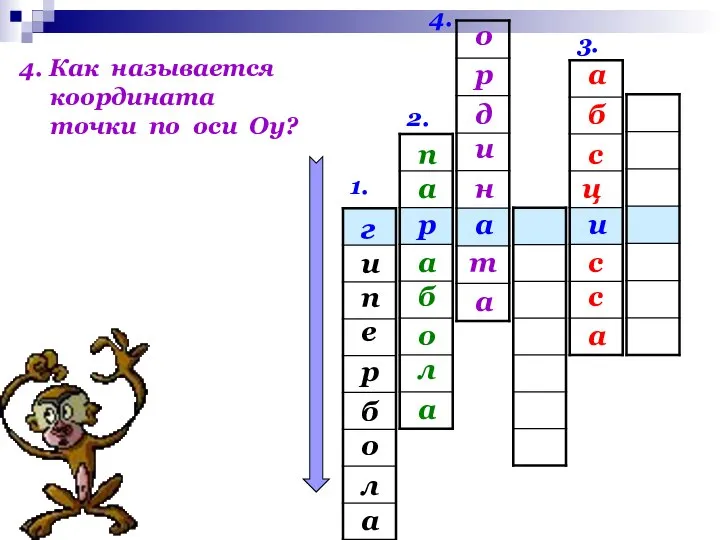
- 22. 1. 2. 3. 4. и а р г и е п а л о б р
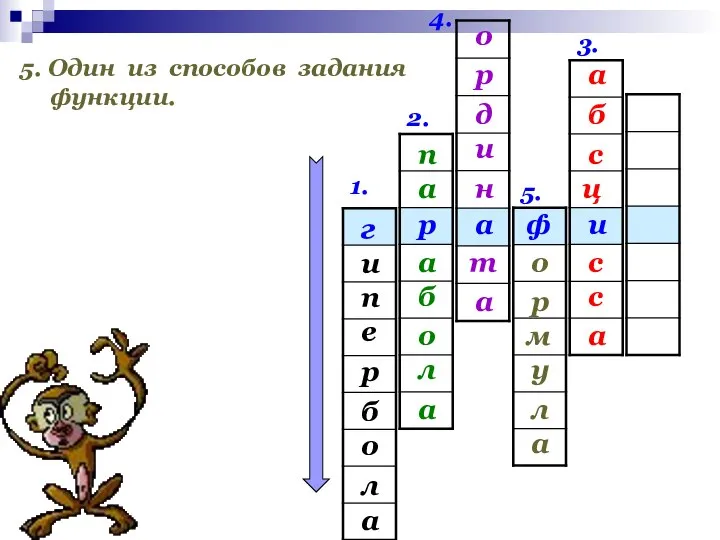
- 23. 1. 2. 3. 4. 5. и ф а р г и е п а л о
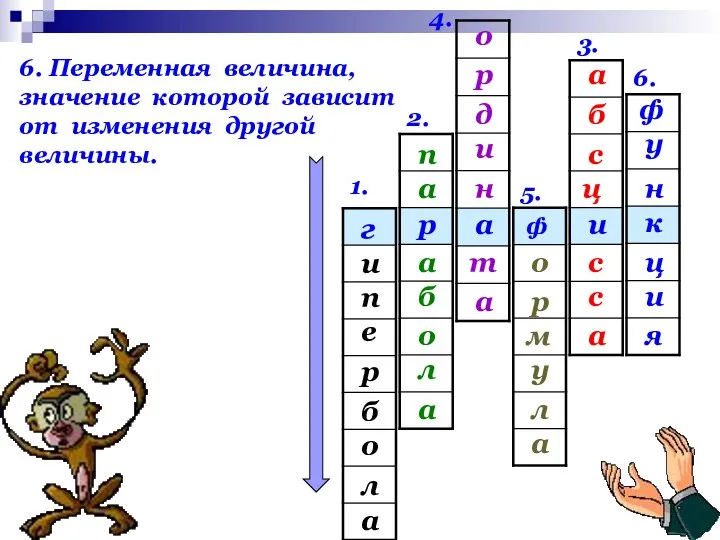
- 24. 1. 2. 3. 4. 5. 6. и ф а р г и е п а л
- 26. Скачать презентацию







 Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Исследование функции с помощью производной и построение графика функции
Исследование функции с помощью производной и построение графика функции Акула. Примеры
Акула. Примеры Линейная функция
Линейная функция Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Презентация на тему Наибольший общий делитель, наименьшее общее кратное
Презентация на тему Наибольший общий делитель, наименьшее общее кратное  Построение графика функции
Построение графика функции Математическая раскраска
Математическая раскраска Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Математические приемы быстрого счета (лайфхаки)
Математические приемы быстрого счета (лайфхаки) Цикломатика графов
Цикломатика графов Профильная математика № 17
Профильная математика № 17 Производная степенной функции. Производная и её геометрический смысл
Производная степенной функции. Производная и её геометрический смысл Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Эволюционные этапы развития логистики
Эволюционные этапы развития логистики Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)
Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)  Аксиомы стереометрии
Аксиомы стереометрии Умножение на 1. Проведите динозаврика по лабиринту (1)
Умножение на 1. Проведите динозаврика по лабиринту (1) Определитель второго порядка
Определитель второго порядка Пропорциональность величин
Пропорциональность величин Построение графика функции
Построение графика функции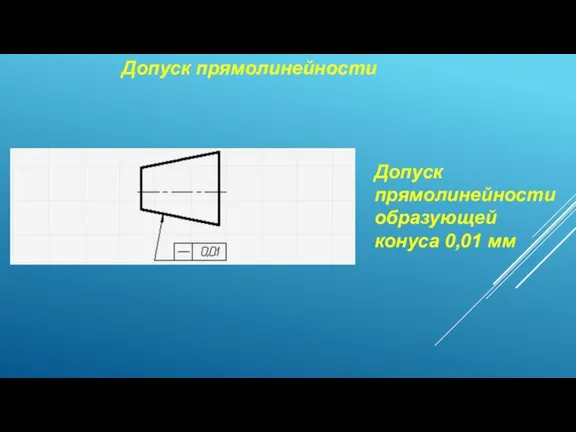 Допуск прямолинейности
Допуск прямолинейности Множення і ділення десяткових дробів. 5 клас
Множення і ділення десяткових дробів. 5 клас Что такое проекция вектора
Что такое проекция вектора У гостях у Цвіріньчика
У гостях у Цвіріньчика Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1)