Презентация на тему Угол вписанный в окружность

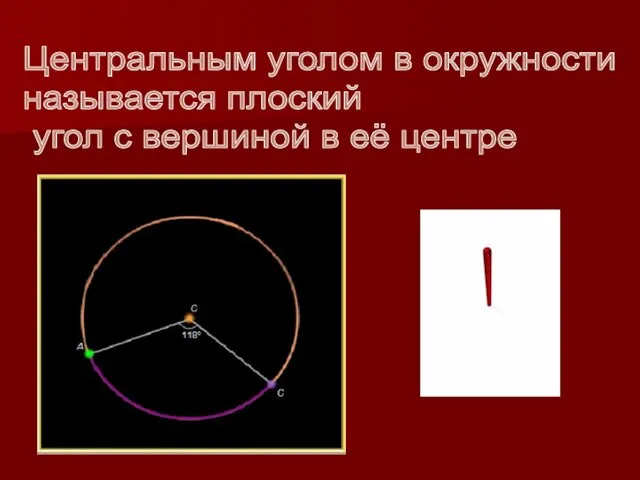
Центральным уголом в окружности
называется плоский угол с вершиной в её центре

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность

Теорема 11.5. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Док-во.
Рассмотрим сначала частный случай, когда одна из сторон угла проходит через центр окружности. Треугольник АОВ равнобедренный, так как у него стороны OA и ОВ равны как радиусы. Поэтому углы А и В треугольника равны. А так как их сумма равна внешнему углу треугольника при вершине О, то угол В треугольника равен половине угла АОС, что и требовалось доказать

Свойства отрезков пересекающихся хорд
и свойства отрезков секущих
1.Если хорды
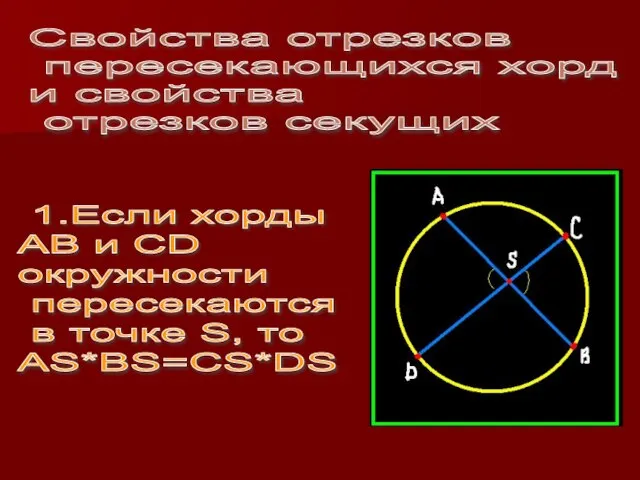
АВ и СD
окружности пересекаются в точке S, то
AS*BS=CS*DS