Прикладная статистика. Доверительные интервалы для среднего. Критерий t Стьюдента. Критерии Уилкоксона для ранговых сравнений

Стандартное отклонение распределения выборочных средних

Стандартное отклонение распределения выборочных средних

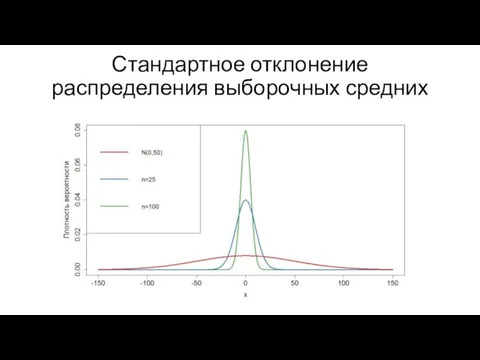
z - доверительный интервал для среднего

Статистические сравнения

z - тест значимости разницы среднего распределения и заданной константы

z тест значимости разницы двух средних

Семейство распределений t Стьюдента

Нормальное и t распределения

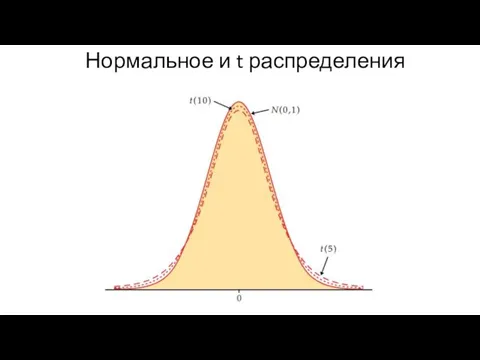
t доверительный интервал для одной выборки

t тест для одной выборки (сравнение с константой)

t тест для парных выборок
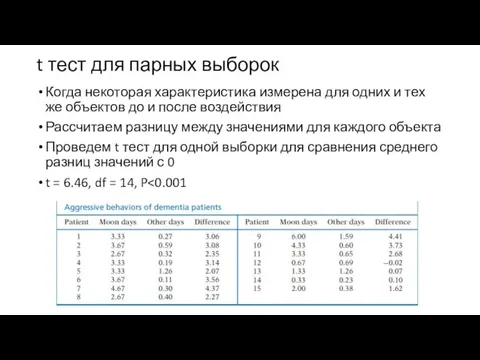
Когда некоторая характеристика измерена для одних и тех же объектов до и после воздействия
Рассчитаем разницу между значениями для каждого объекта
Проведем t тест для одной выборки для сравнения среднего разниц значений с 0
t = 6.46, df = 14, P<0.001

Постановка задачи для двух независимых выборок
Задача – сравнить эффект между двумя группами
Каждая группа представляет из себя случайную выборку из двух различных распределений
Эффект в одной группе не зависит от эффекта в другой группе

t тест Уэлча для двух выборок

t тест Уэлча для двух выборок

Доверительный интервал Уэлча для разницы средних

t тест с объединенной оценкой дисперсии

U тест суммы рангов Уилкоксона-Манна-Уитни

Пример: урожай на двух площадках с сорняками и без

Тест связанных рангов Уилкоксона

Пример: способность детей запоминать сказки с картинками и без

Что тестируют ранговые тесты?

Методы расчета P-значения ранговых тестов
Точный метод. Лучший. Перебор всех возможных комбинаций данных для построения точного распределения нужной статистики. При больших выборках не выполним из-за слишком большого времени вычисления
Алгоритмы Монте Карло: пермутационные тесты сравнений и соответствующие им бутстреп – доверительные интервалы для любых статистик. По сути – перебор ограниченного случайного числа комбинаций. Позволяют получить P – значение с заданной точностью. Хороши для больших выборок
Аппроксимация W статистики нормальным распределением – самый простой, но самый ненадежный способ. Тем не менее, зачастую хорошо работает при больших выборках

Как проверить нормальность распределения?
Графики нормальных квантилей
(Q-Q плоты, могут быть для
разных распределений)
Формальные тесты:
их множество, но самые
распространенные – это
тесты Андерсона-Дарлинга
и Шапиро-Уилка

Ошибки первого и второго рода
Ошибка 1 рода происходит, когда мы отвергаем нулевую гипотезу (принимаем альтернативную), когда она правильная*
Ошибка 2 рода происходит, когда мы не отвергаем нулевую гипотезу, когда альтернативная гипотеза правильная*
* Chihara Laura and Tim Hesterberg. Mathematical statistics with resampling and R. John Wiley & Sons, 2012.

Корректировка на множественные сравнения