Содержание
- 2. Первый признак подобия треугольников ЕСЛИ ДВА УГЛА ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ДВУМ УГЛАМ ДРУГОГО, ТО ТАКИЕ
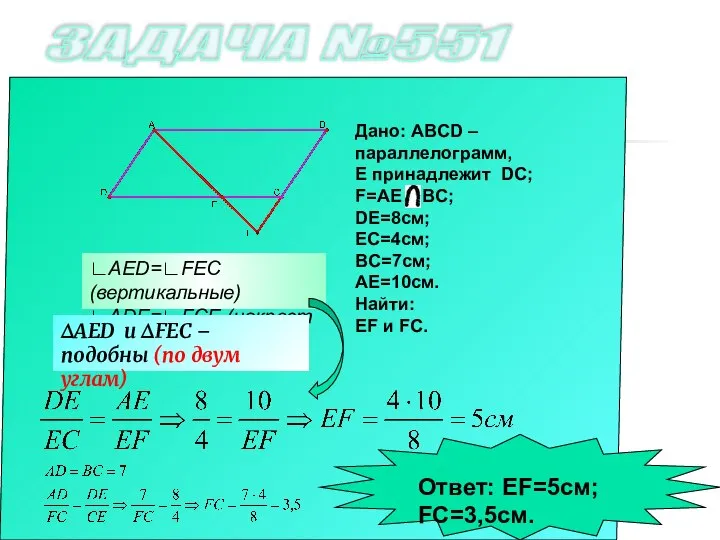
- 3. ЗАДАЧА №551 Дано: ABCD – параллелограмм, Е принадлежит DC; F=AE BC; DE=8см; EC=4см; BC=7см; AE=10см. Найти:
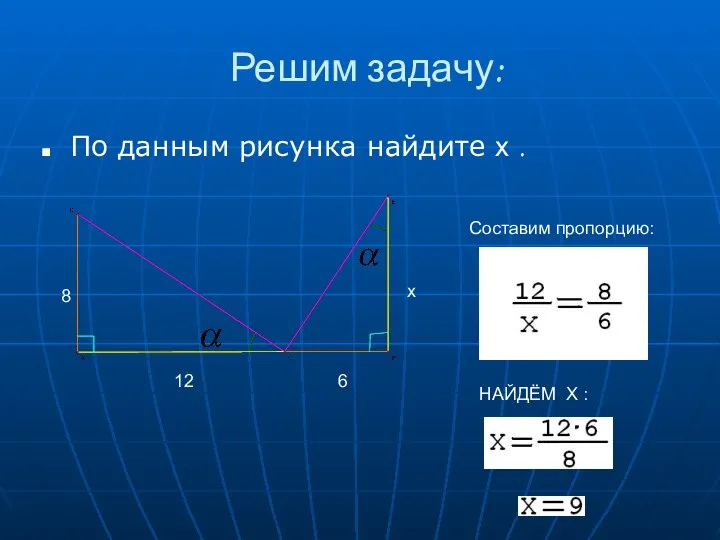
- 4. Решим задачу: По данным рисунка найдите х . 8 12 6 х Составим пропорцию: НАЙДЁМ Х
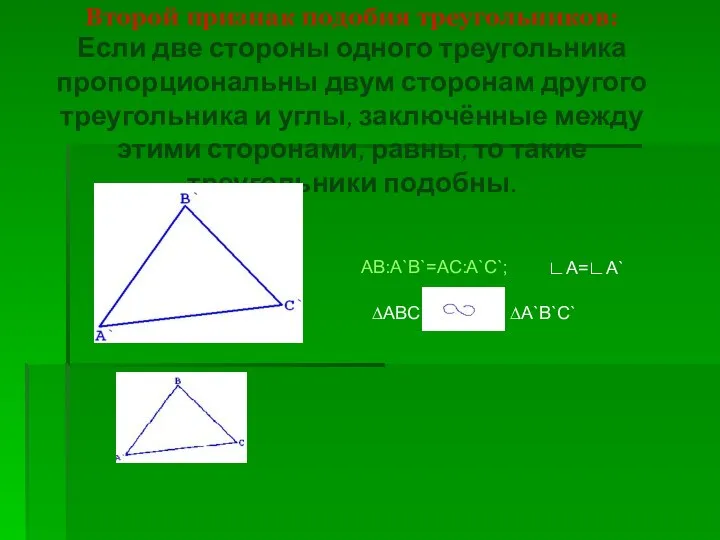
- 5. Второй признак подобия треугольников: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы,
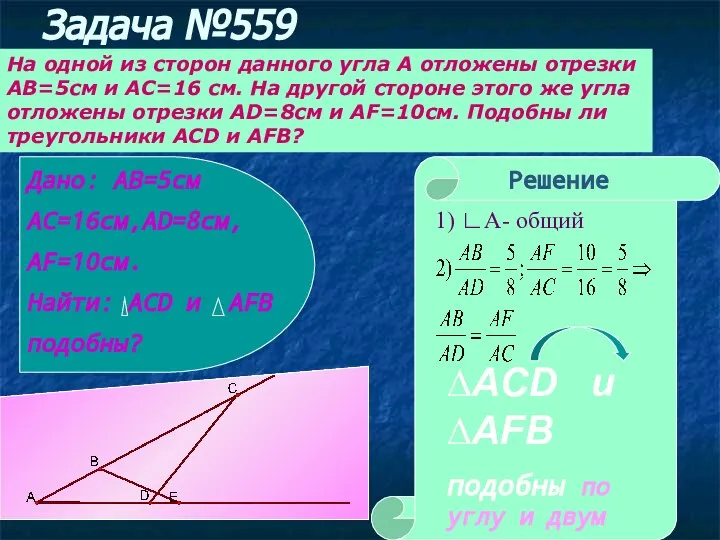
- 6. Задача №559 На одной из сторон данного угла А отложены отрезки АВ=5см и АС=16 см. На
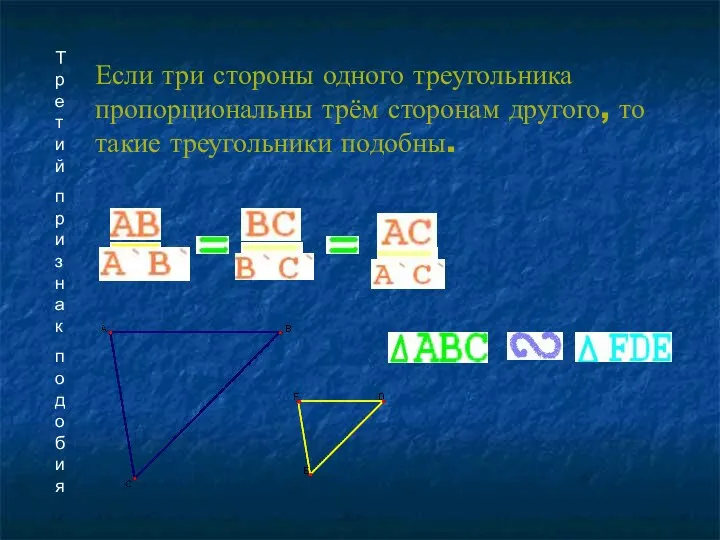
- 7. Третий признак подобия Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
- 8. Подобны ли треугольники ABC и A1B1C1, если АВ=3см, ВС=5см, СА=7см, А1В1=4,5см, В1С1=7,5см, С1А1=10,5см? Задача №560 Решение
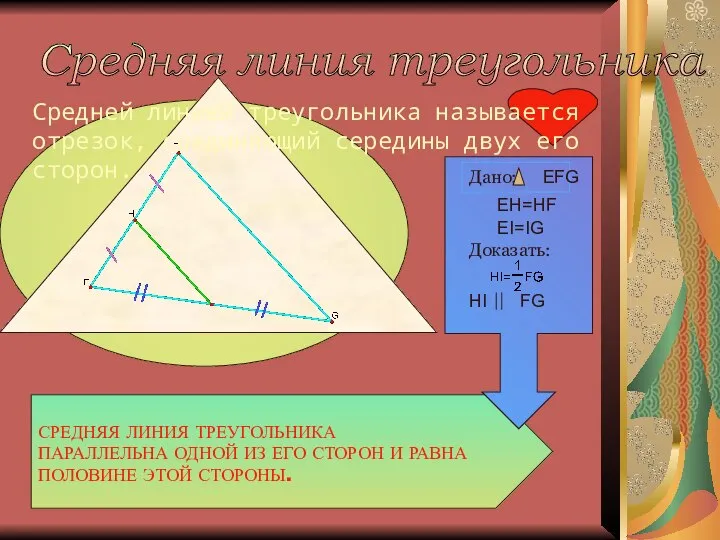
- 9. Средняя линия треугольника Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
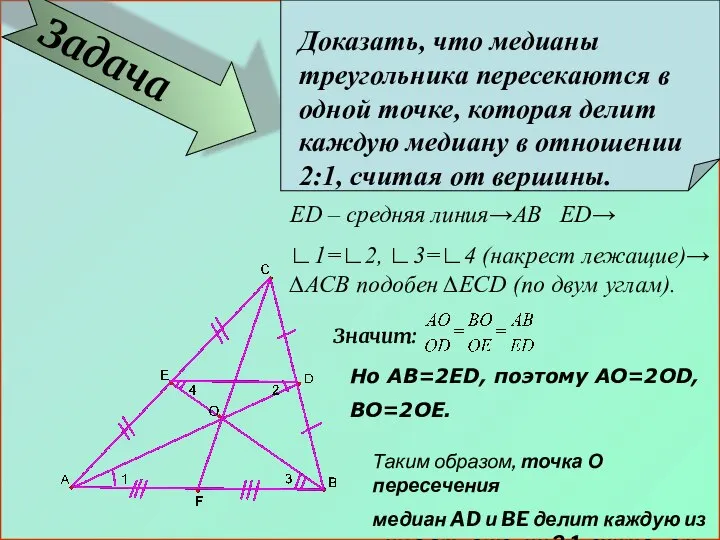
- 10. Задача Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1,
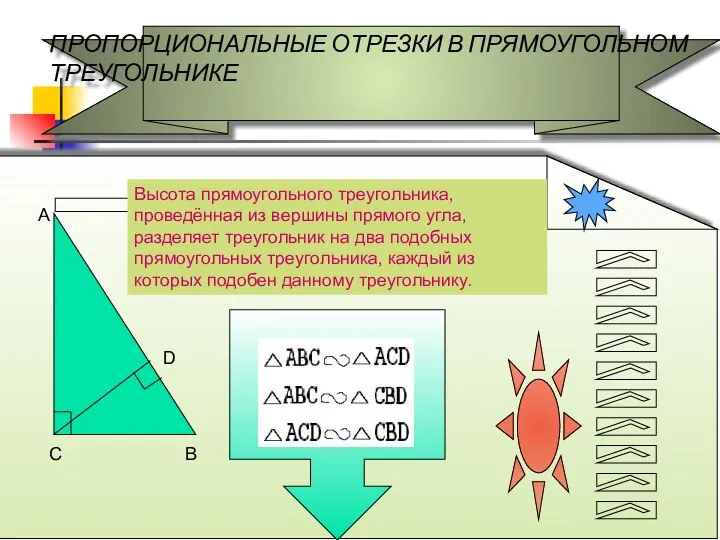
- 11. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ А В D Высота прямоугольного треугольника, проведённая из вершины прямого угла,
- 12. 1. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые
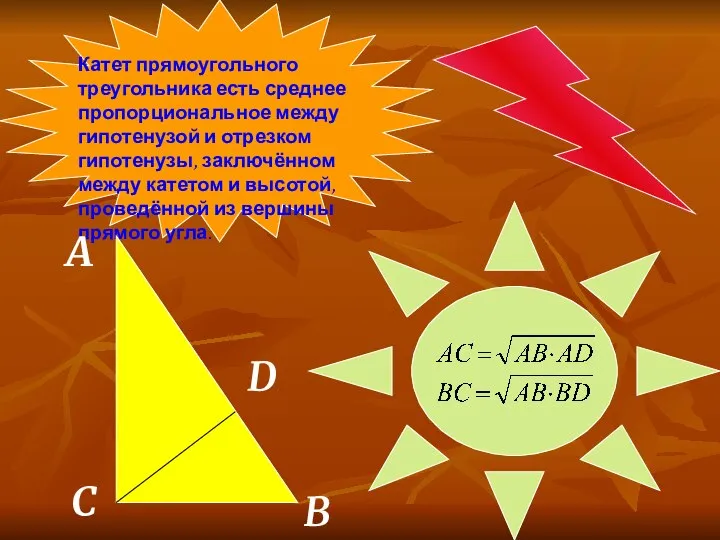
- 13. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённом между катетом и высотой,
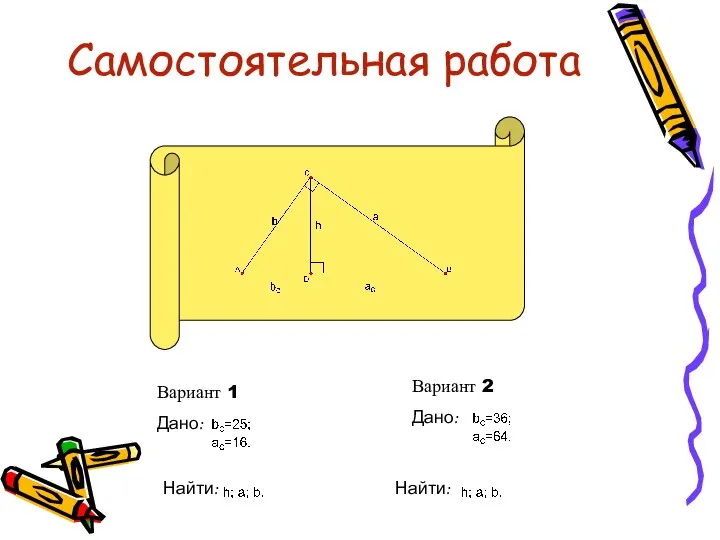
- 14. Самостоятельная работа Вариант 1 Дано: Вариант 2 Дано: Найти: Найти:
- 16. Скачать презентацию



 Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений
Сложение и вычитание дробей с одинаковыми знаменателями. Решение уравнений Правила деления. (6 класс)
Правила деления. (6 класс) Векторы. 9 класс
Векторы. 9 класс Вторая производная и её физический смысл
Вторая производная и её физический смысл Повторение. Дроби
Повторение. Дроби Презентация на тему Арифметическая прогрессия в древности
Презентация на тему Арифметическая прогрессия в древности  Математический дизайн
Математический дизайн Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Основы моделирования
Основы моделирования Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика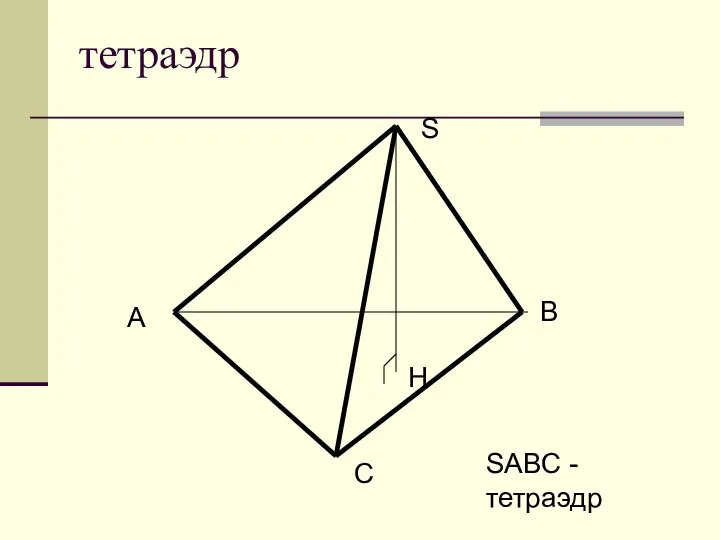 Тетраэдр
Тетраэдр Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда ОДУ высших порядков
ОДУ высших порядков Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Признаки равенства треугольников. Подготовка к контрольной работе
Признаки равенства треугольников. Подготовка к контрольной работе Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс
Презентация на тему Вычитание и сказка "Царевна-лягушка" 2 класс  Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением
Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением ВПР - 7- 9 класс
ВПР - 7- 9 класс Математика в биологии
Математика в биологии Уравнение вида ах2 + bx + c = 0,
Уравнение вида ах2 + bx + c = 0, Прямоугольный треугольник. Задачи. 7 класс
Прямоугольный треугольник. Задачи. 7 класс Историческая задача
Историческая задача Биометрия, как наука
Биометрия, как наука Решение задач (2 класс)
Решение задач (2 класс) Решение квадратных уравнений содержащих параметры в 9 классе
Решение квадратных уравнений содержащих параметры в 9 классе Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)  Контрольная работа. Геометрия
Контрольная работа. Геометрия