Нахождение угла между скрещивающимися прямыми

Аргументы.
1). Определение скрещивающихся прямых.
2). Определение угла между скрещивающимися прямыми.
3). Признак скрещивающихся прямых.
4). Теорема Пифагора.
5). Свойство высоты равнобедренного треугольника, проведенной
к основанию.
6). Определение правильной призмы.
7). Определение синуса острого угла прямоугольного треугольника.
8). Определение косинуса острого угла прямоугольного треугольника.
9). Определение правильного многоугольника.
10). Теорема о сумме углов выпуклого многоугольника.
11). Свойство окружности, описанной около правильного шестиугольника.

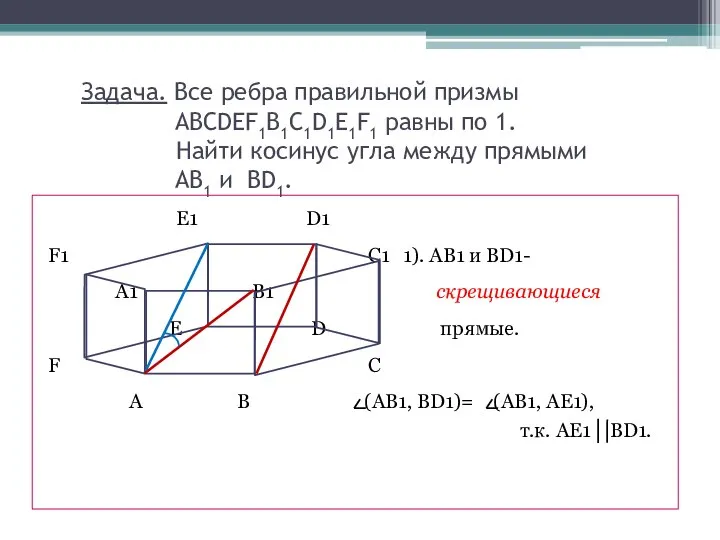
Задача. Все ребра правильной призмы
ABCDEF1B1C1D1E1F1 равны по 1.
Найти косинус угла между прямыми
AB1 и BD1.
E1 D1
F1 C1 1). AB1 и BD1-
A1 B1 скрещивающиеся
E D прямые.
F C
A B (AB1, BD1)= (AB1, AE1),
т.к. AE1│ BD1.

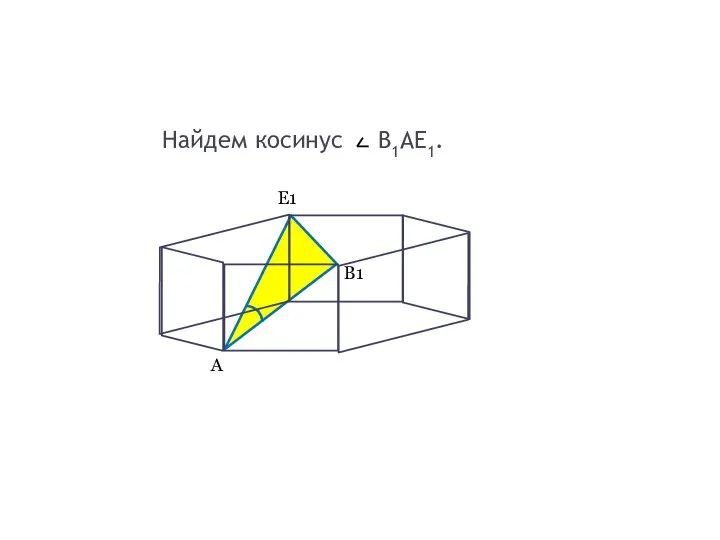
Найдем косинус B1AE1.
А
В1
Е1

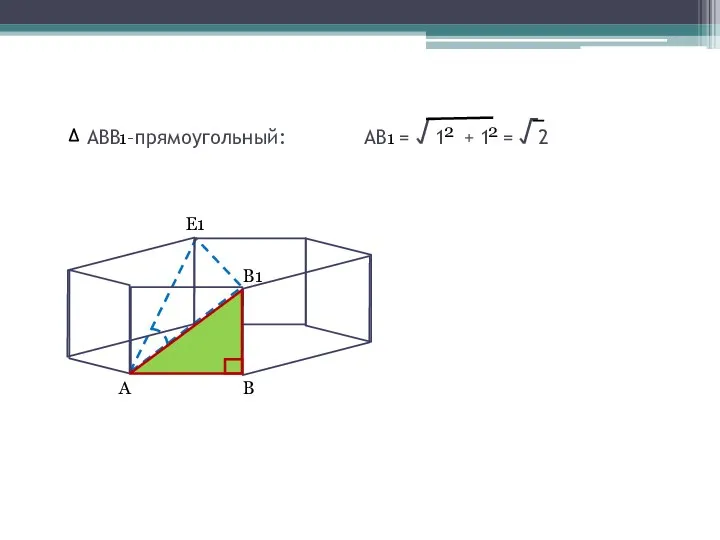
АВВ –прямоугольный: АВ = √1 + 1 = √2
1
1
2
2
А
В1
В
Е1

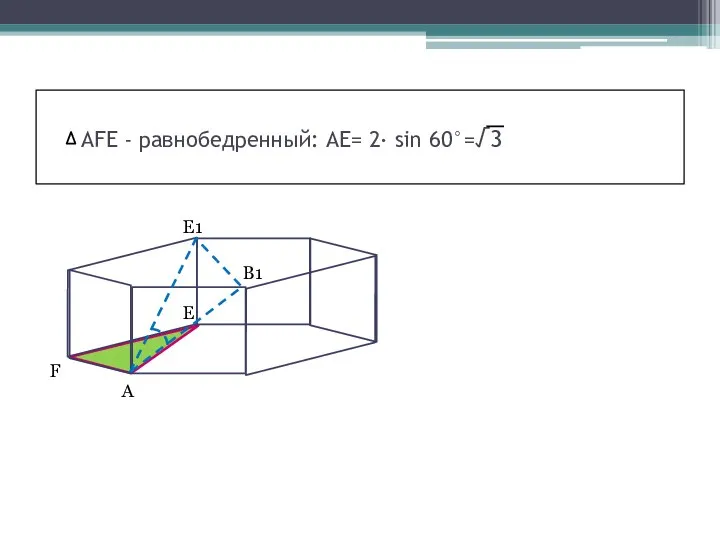
AFE - равнобедренный: АЕ= 2· sin 60°=√3
F
A
E
E1
В1

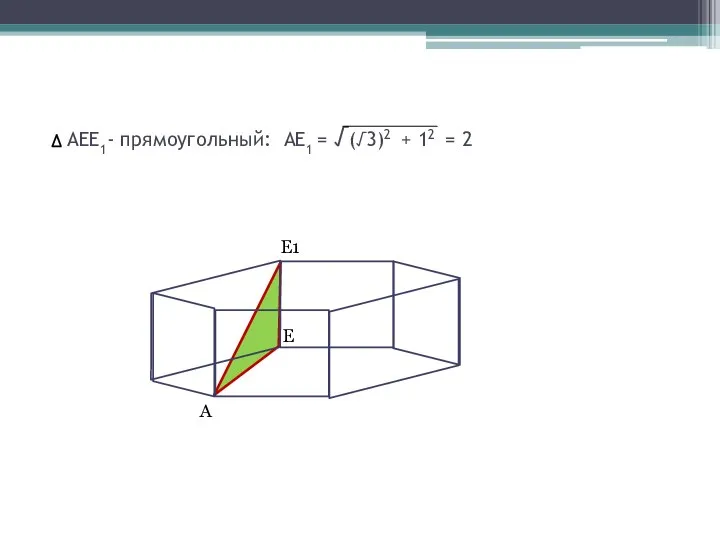
AEE1- прямоугольный: АЕ1 = √(√3)2 + 12 = 2
E1
A
E

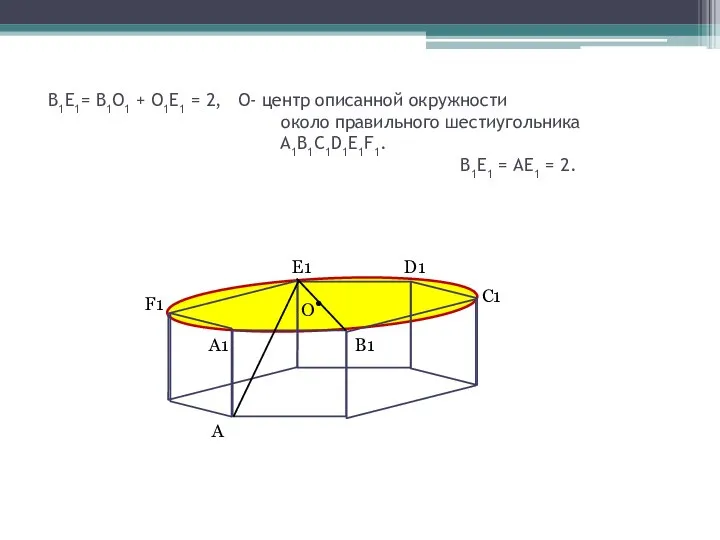
В1Е1= В1О1 + О1Е1 = 2, О- центр описанной окружности
около правильного шестиугольника
A1B1C1D1E1F1.
В1Е1 = АЕ1 = 2.
F1
E1
D1
B1
C1
A1
O
A