Применение производной для исследования функции на монотонность и экстремумы

Применение производной для исследования функции на монотонность и экстремумы

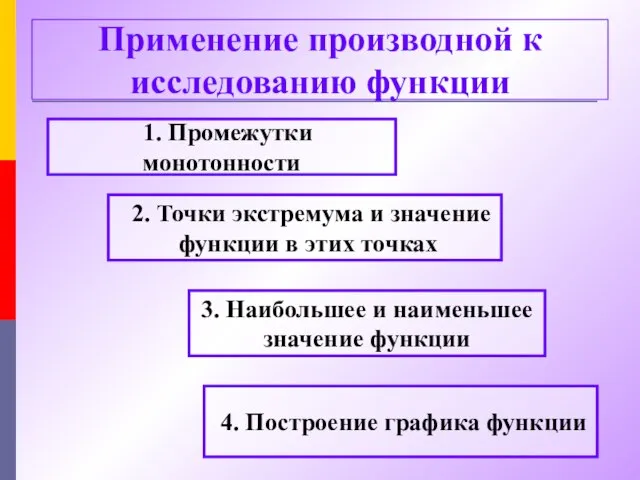
Применение производной к исследованию функции
1. Промежутки монотонности
3. Наибольшее и наименьшее
значение функции
2. Точки экстремума и значение
функции в этих точках
4. Построение графика функции

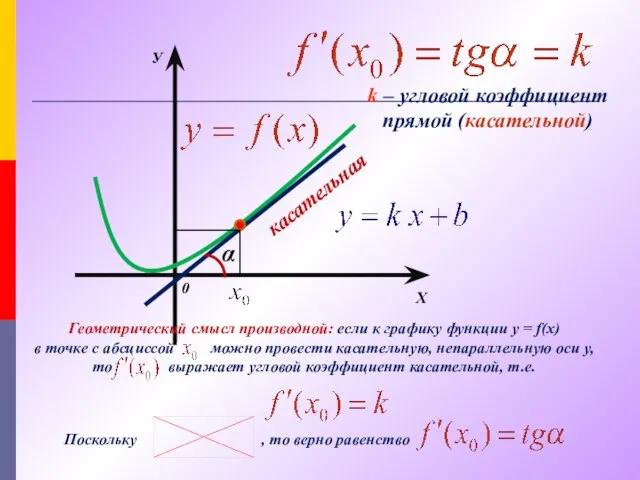
Х
У
0
касательная
α
k – угловой коэффициент прямой (касательной)
Геометрический смысл производной: если к графику функции y = f(x)
в точке с абсциссой можно провести касательную, непараллельную оси у,
то выражает угловой коэффициент касательной, т.е.
Поскольку , то верно равенство

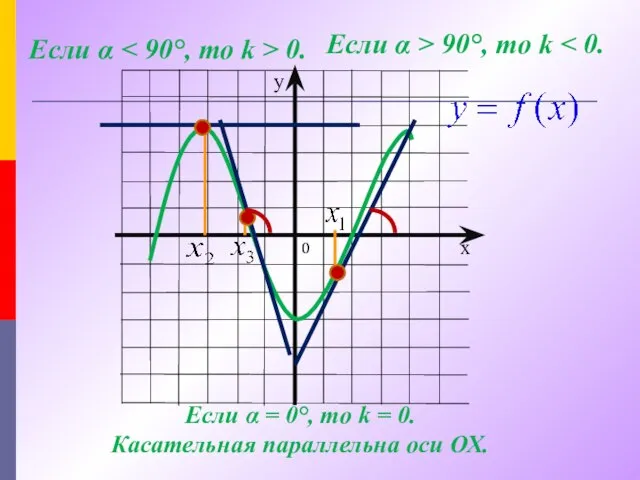
Если α < 90°, то k > 0.
Если α > 90°, то k < 0.
Если α = 0°, то k = 0.
Касательная параллельна оси ОХ.
0

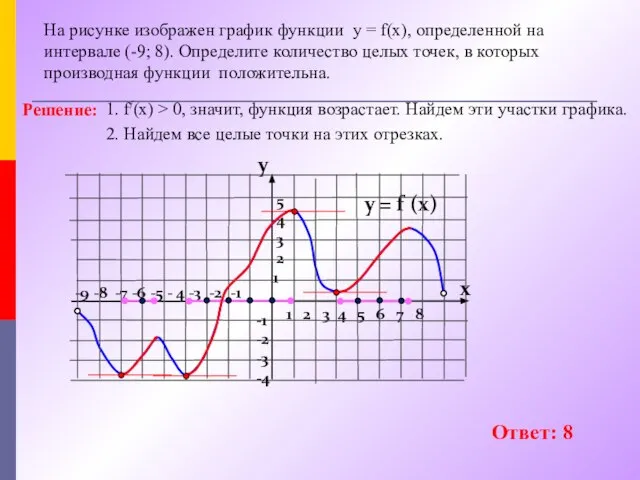
Монотонность функции
Если производная функции y=f(x) положительна на некотором интервале, то функция в этом интервале монотонно возрастает
Если производная функции y=f(x) отрицательна на некотором интервале, то функция в этом интервале монотонно убывает.

-9 -8 -7 -6 -5 - 4 -3 -2 -1
1 2 3 4 5 6 7 8
На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 8
Решение:

-9 -8 -7 -6 -5 - 4 -3 -2 -1
1 2 3 4 5 6 7 8
На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 5
Решение:

Точки экстремума
Стационарные точки
Критические точки
Если функция y=f(x) имеет экстремум в точке x=x0,
то в этой точке производная функции
или равна нулю, или не существует
Касательная в
таких точках графика
не существует
Касательная
в таких точках
графика параллельна оси ОХ

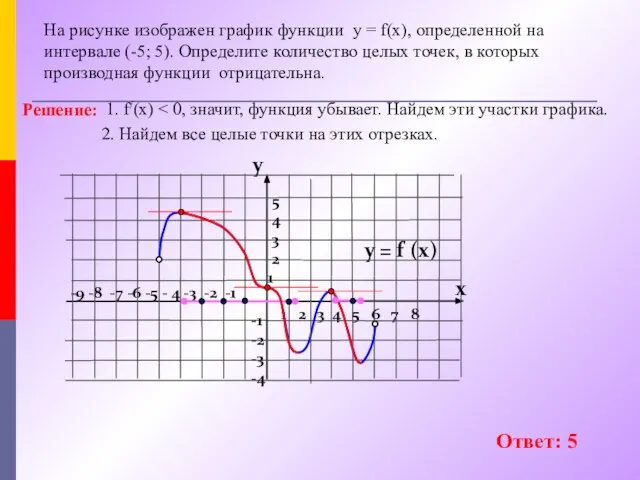
Непрерывная функция у = f(x) задана на отрезке [a;b]
На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.
y = f(x)
y
x
Ответ: 5
a
b

Достаточное условие существования экстремума функции:
Если при переходе через стационарную точку х0 функции f(x) ее производная меняет знак с «+» на «-», то х0 – точка максимума функции f(x).
Если при переходе через стационарную точку х0 функции f(x) ее производная меняет знак с «-» на «+», то х0 – точка минимума функции f(x).
Если при переходе через стационарную точку х0 функции f(x) ее производная не меняет знака, то в точке х0 экстремума нет.

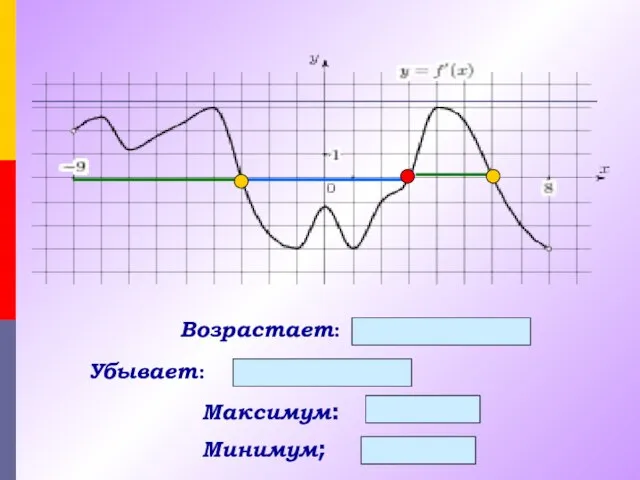
Максимум: - 3; 6
Минимум; 3
Возрастает: (-9;-3) и (3;6)
Убывает: (-3;3)

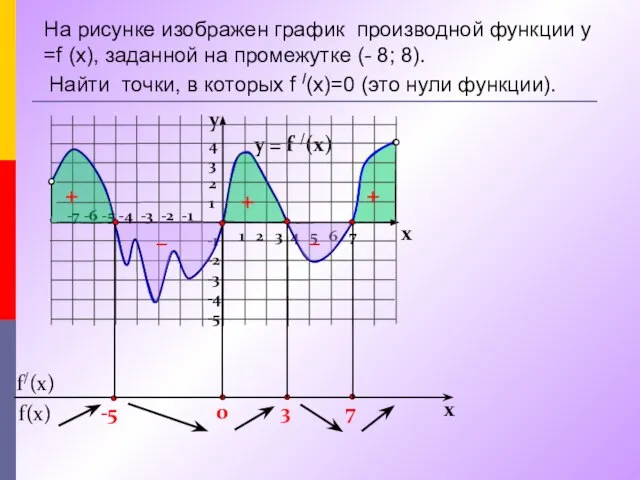
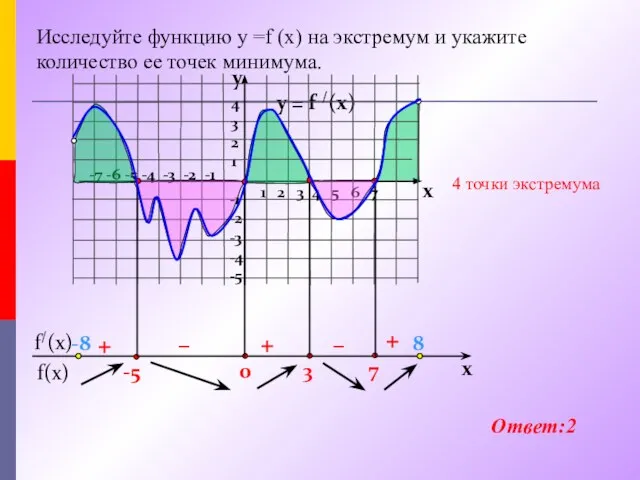
На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8).
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Найти точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+

y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
4 точки экстремума
Ответ:2
-8
8

y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Найдите количество точек экстремума функции у =f (x)
на отрезке [– 3; 7]
Ответ: 3
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-8
8

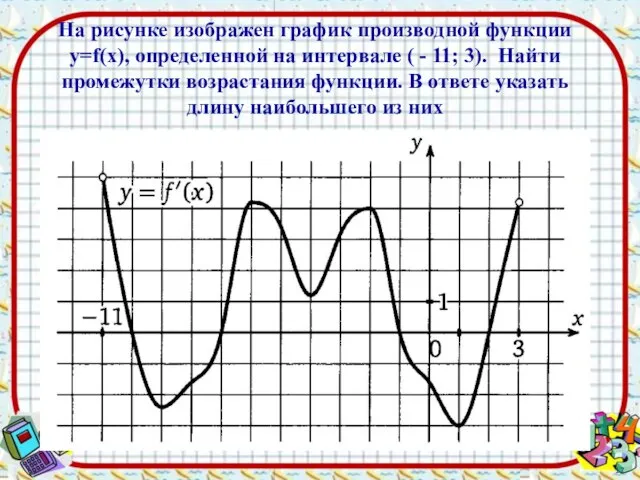
На рисунке изображен график производной функции y=f(x), определенной на интервале ( - 11; 3). Найти промежутки возрастания функции. В ответе указать длину наибольшего из них

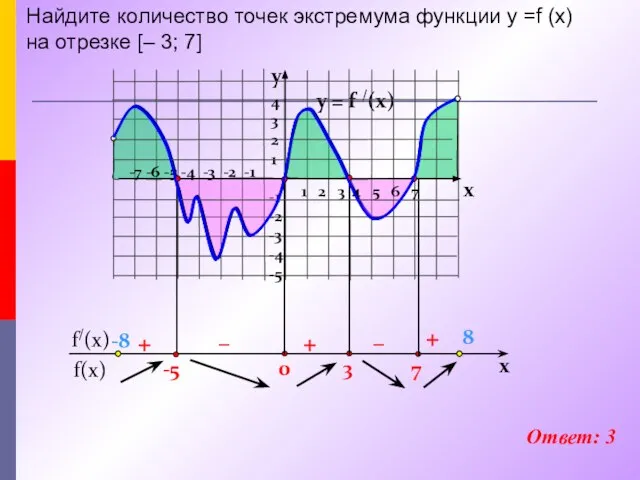
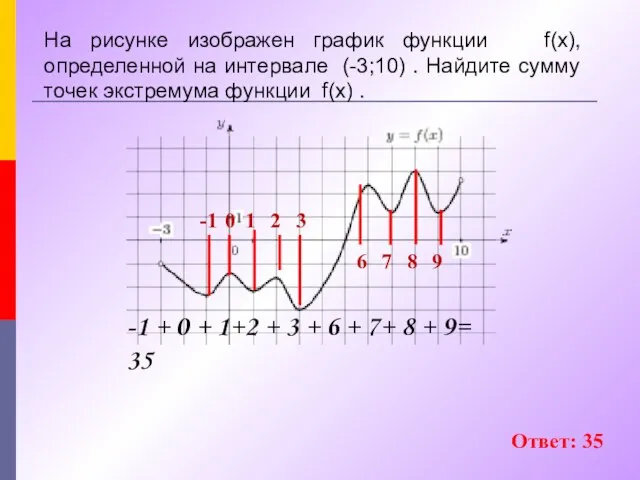
На рисунке изображен график функции f(x), определенной на интервале (-3;10) . Найдите сумму точек экстремума функции f(x) .
-1
0
1
3
6
7
8
9
-1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35
Ответ: 35
2

Исследование функции на монотонность
Найти производную f ´.
Найти стационарные и критические точки
функции f (х).
Отметить промежутки знакопостоянства f ´.
и промежутки монотонности функции f (х).
Найти D(f) и исследовать на непрерывность
функцию f (х).

Область определения: R. Функция непрерывна.
Вычисляем производную : y’=6x²-6x-36.
Находим стационарные точки: y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
Найти промежутки монотонности функции y=2x³-3x²-36x+5
-2
3
+
-
+
5.Функция возрастает при xϵ (-∞; -2)υ(3; +∞),
функция убывает при xϵ (-2; 3).

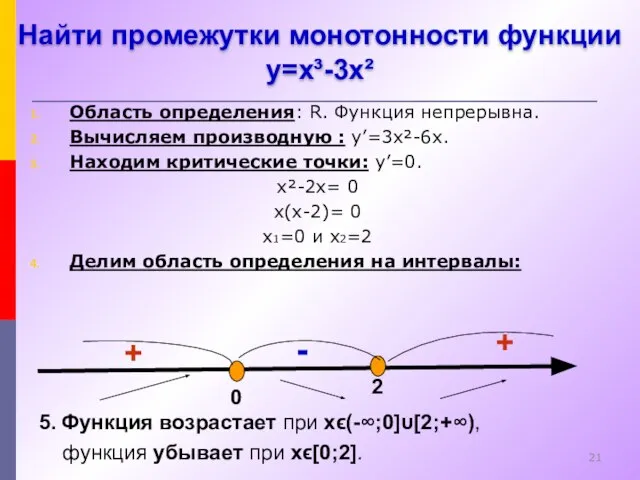
Область определения: R. Функция непрерывна.
Вычисляем производную : y’=3x²-6x.
Находим критические точки: y’=0.
x²-2x= 0
x(x-2)= 0
x1=0 и x2=2
Делим область определения на интервалы:
Найти промежутки монотонности функции y=x³-3x²
0
2
-
+
5. Функция возрастает при xϵ(-∞;0]υ[2;+∞),
функция убывает при xϵ[0;2].
+

Алгоритм исследования функции f(х) на экстремум с помощью производной :
Найти D(f) и исследовать на непрерывность функцию f (х).
Найти производную f ´
Найти стационарные и критические точки функции f(х) и на координатной прямой отметить промежутки знакопостоянства f ´.
Посмотрев на рисунок знаков f ´, определить точки минимума и максимума функции и вычислить значения f(х) в этих точках.

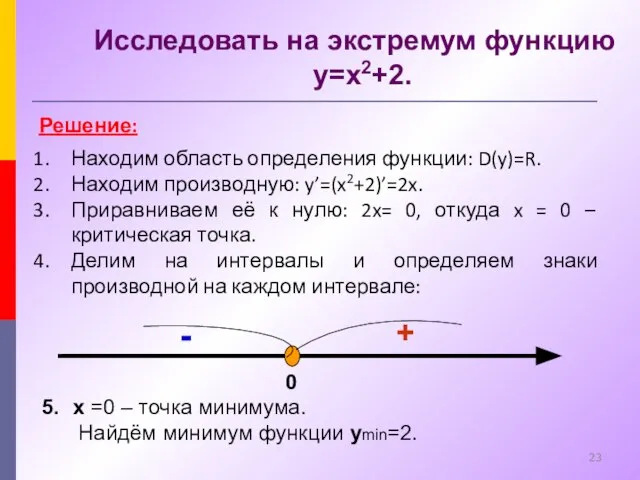
Исследовать на экстремум функцию y=x2+2.
Решение:
Находим область определения функции: D(y)=R.
Находим производную: y’=(x2+2)’=2x.
Приравниваем её к нулю: 2x= 0, откуда x = 0 – критическая точка.
Делим на интервалы и определяем знаки производной на каждом интервале:
0
-
+
х =0 – точка минимума.
Найдём минимум функции ymin=2.

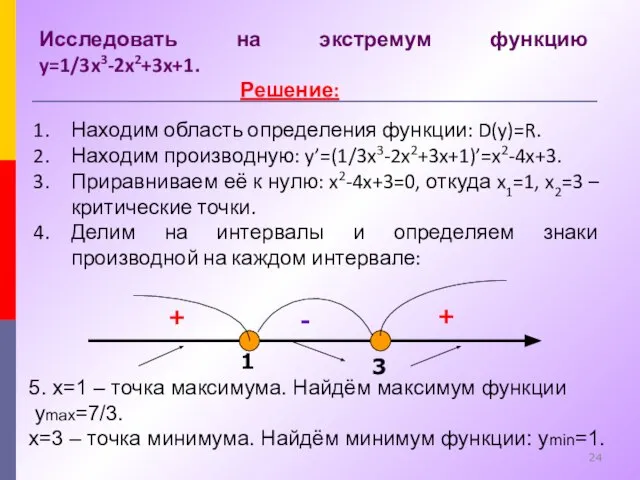
Исследовать на экстремум функцию
y=1/3x3-2x2+3x+1.
Решение:
Находим область определения функции: D(y)=R.
Находим производную: y’=(1/3x3-2x2+3x+1)’=x2-4x+3.
Приравниваем её к нулю: x2-4x+3=0, откуда x1=1, x2=3 – критические точки.
Делим на интервалы и определяем знаки производной на каждом интервале:
5. x=1 – точка максимума. Найдём максимум функции
ymax=7/3.
x=3 – точка минимума. Найдём минимум функции: ymin=1.
1
3
+
+
-

Общая схема исследования функции
Найти область определения функции f(х).
Выяснить, обладает ли функция особенностями, облегчающими исследование, то есть является ли функция f(х):
а) четной или нечетной;
б) периодической.
Вычислить координаты точек пересечения графика с осями координат.
Найти промежутки знакопостоянства производной функции f(х) .
Выяснить, на каких промежутках функция f (х) возрастает, а на каких убывает.
Найти точки экстремума (максимум или минимум) и вычислить значения f (х) в этих точках.
Исследовать поведение функции f (х) в окрестности характерных точек не входящих в область определения.
Построить график функции.

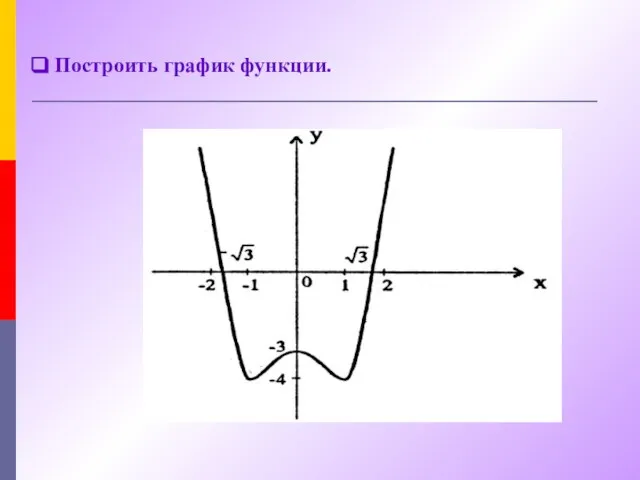
Исследовать функцию f(x)=x4-2x2-3
Область определения: D (f)=R
Четность – нечетность функции: f (-x)=x4-2x2-3,
значит f (-x) = f (x) для любого х, принадлежащего D (f) – функция является чётной.
Координаты точек пересечения графика с осями координат
с ось Оу: f(x)=0: (x2-3)(x2+1)=0; x=± ;
с осью Ох: f(0)=-3
Промежутки знакопостоянства производной f’.
f’(x)=4х3-4x=4х(x-1)(x+1) =0 х = -1; 0; 1.

Промежутки монотонности функция f(х).
Точки экстремума и значения f в этих точках. Составить таблицу.

Построить график функции.

Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b]
Чтобы найти наибольшее и наименьшее значения
непрерывной функции f(x) на промежутке [a;b], нужно
вычислить её значения f(a) и f(b) на концах данного промежутка;
вычислить её значения в точках экстремума, принадлежащих этому промежутку;
Выбрать из них наибольшее и наименьшее.
Записывают : max f(x) и min f(x)
[a;b] [a;b]