Содержание
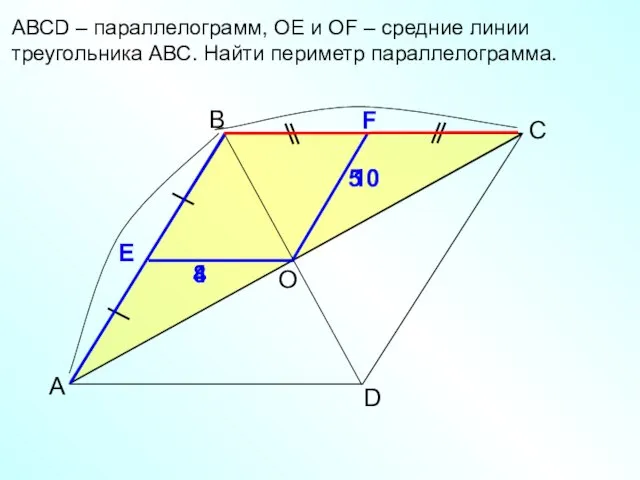
- 2. В А D АВСD – параллелограмм, ОЕ и ОF – средние линии треугольника АВС. Найти периметр
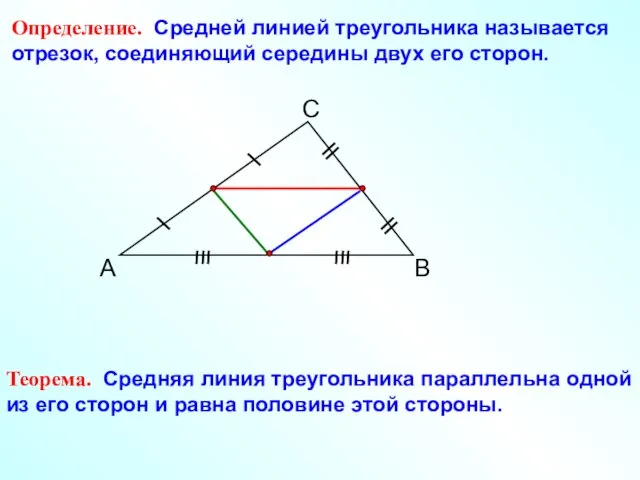
- 3. А С В Определение. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Теорема. Средняя
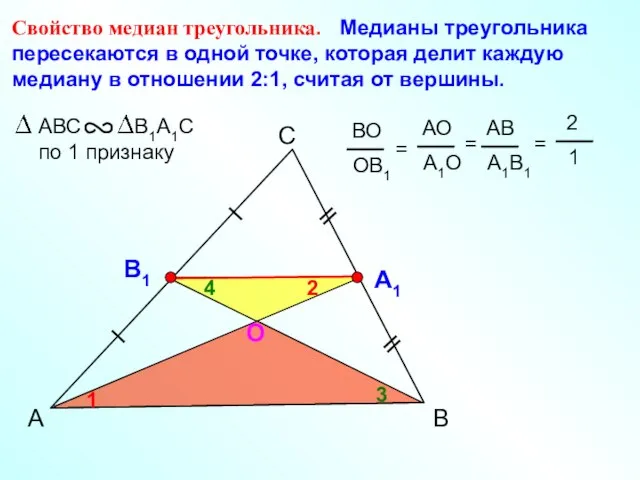
- 4. А С В Свойство медиан треугольника. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану
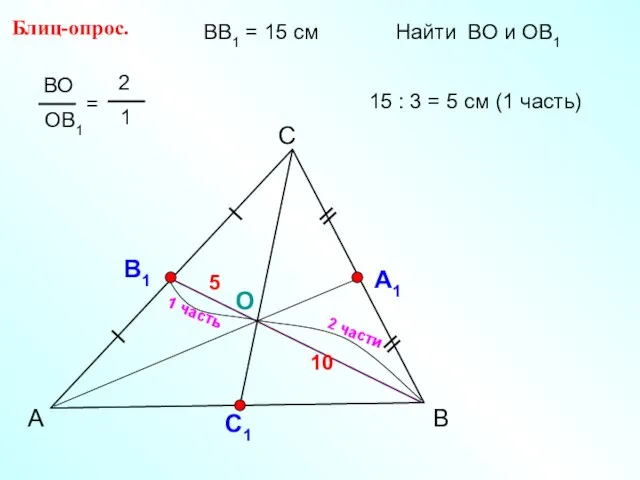
- 5. А С В Блиц-опрос. А1 О С1 ВВ1 = 15 см Найти ВО и ОВ1 15
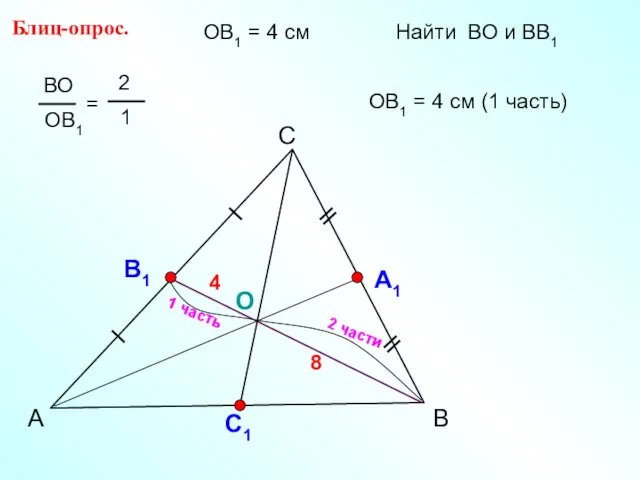
- 6. А С В Блиц-опрос. А1 О С1 ОВ1 = 4 см Найти ВО и ВВ1 ОВ1
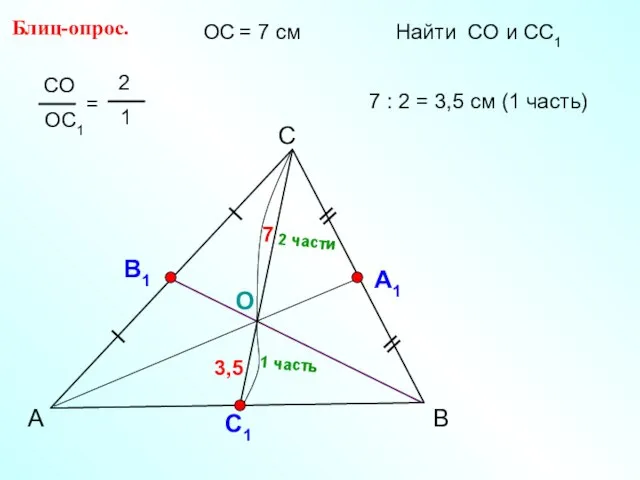
- 7. А С В Блиц-опрос. А1 О С1 ОС = 7 см Найти СО и СС1 7
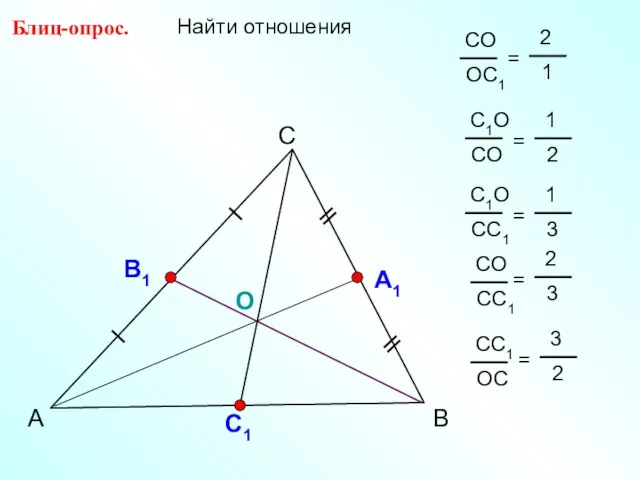
- 8. А С В Блиц-опрос. А1 О С1 Найти отношения
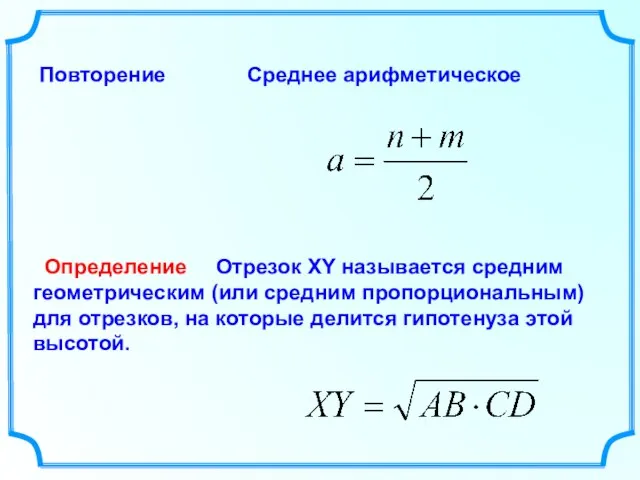
- 9. Определение Повторение Среднее арифметическое Отрезок XY называется средним геометрическим (или средним пропорциональным) для отрезков, на которые
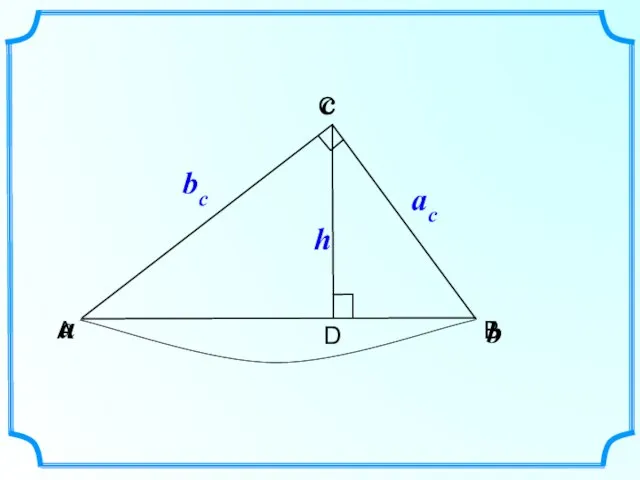
- 10. B C A b a c bc ac h
- 11. B C A D
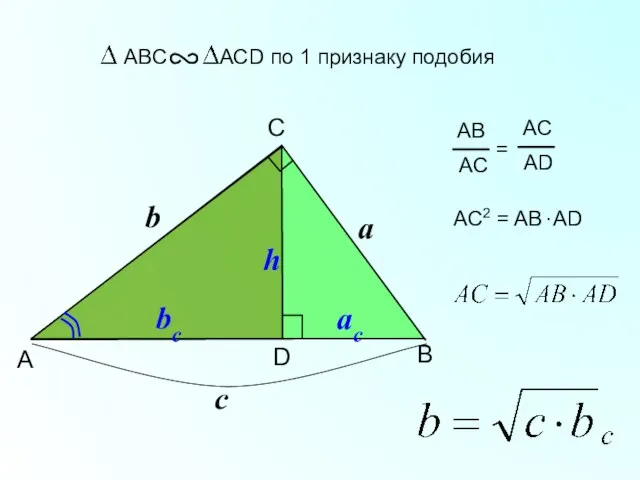
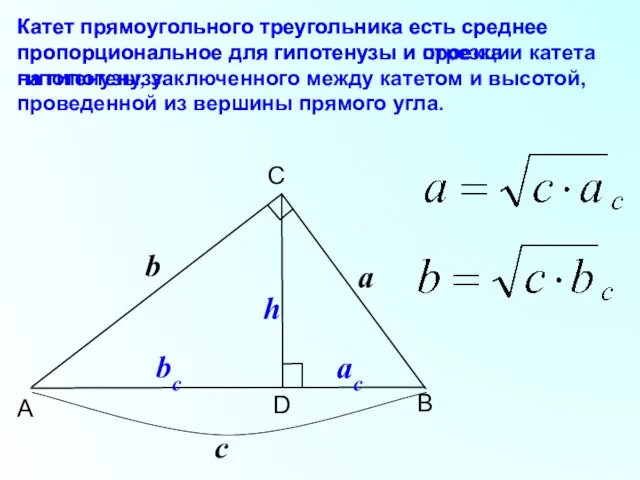
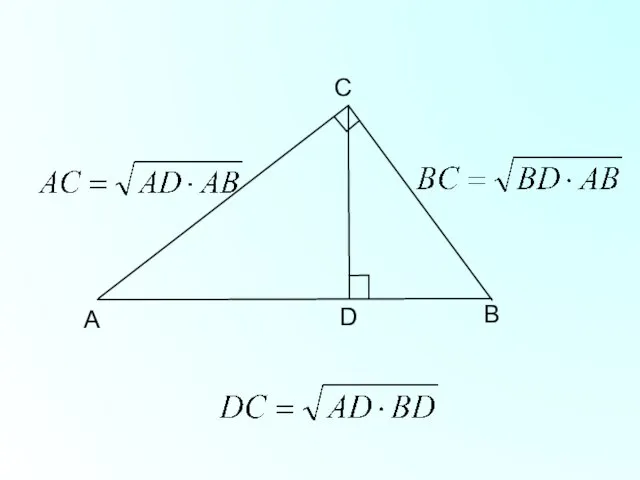
- 12. B C A D Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного
- 13. B C A D
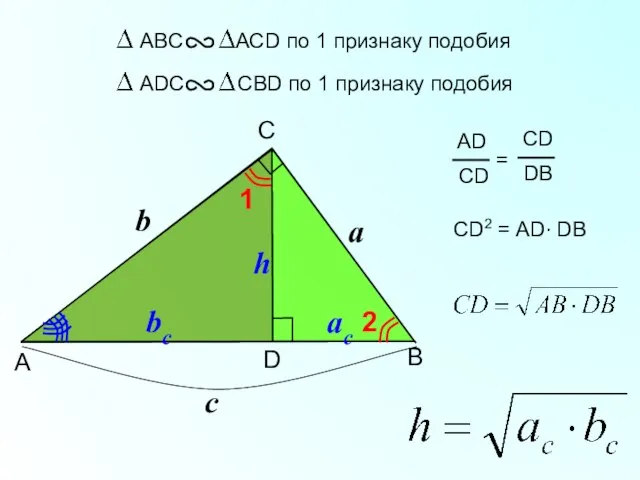
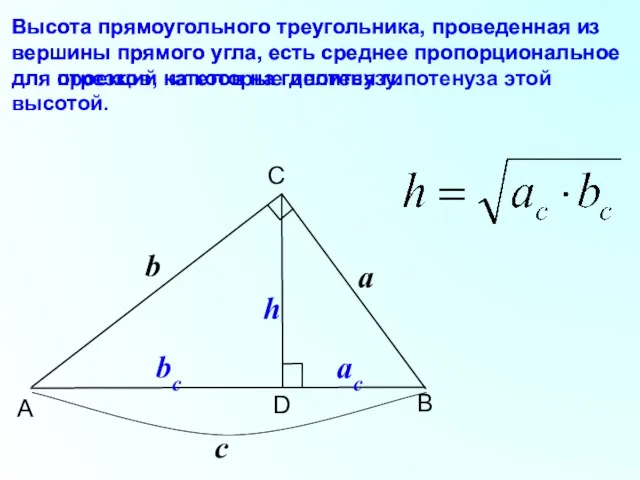
- 14. B C A D Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для
- 15. B C А D
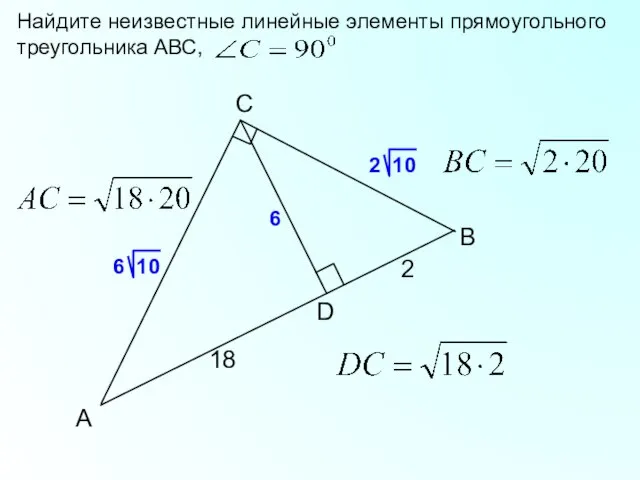
- 16. B C А D 18 2 6
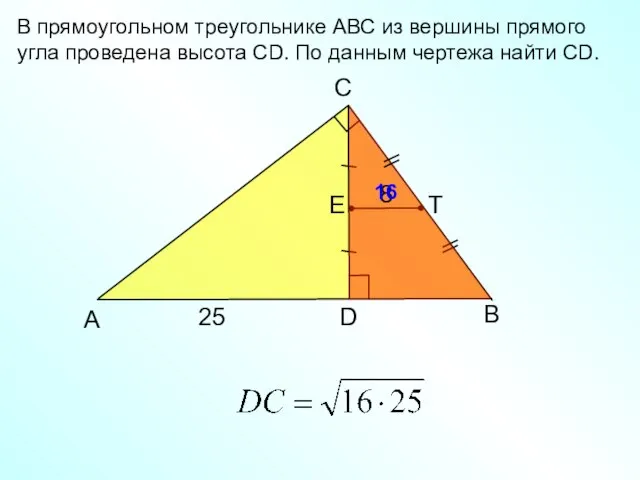
- 17. B C А D 25 В прямоугольном треугольнике АВС из вершины прямого угла проведена высота СD.
- 19. Скачать презентацию
 Строение функции, свойства, графики
Строение функции, свойства, графики Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Проверка умножения делением
Проверка умножения делением Монотонность функции
Монотонность функции Таблица умножения в пределах 100. Урок повторения и закрепления
Таблица умножения в пределах 100. Урок повторения и закрепления Волшебный мир иллюзий
Волшебный мир иллюзий Презентация на тему Слагаемые Сумма
Презентация на тему Слагаемые Сумма  Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем ГИА - 2016. Открытый банк заданий по математике. Задача №15
ГИА - 2016. Открытый банк заданий по математике. Задача №15 Презентация на тему Квадратный сантиметр (3 класс)
Презентация на тему Квадратный сантиметр (3 класс) 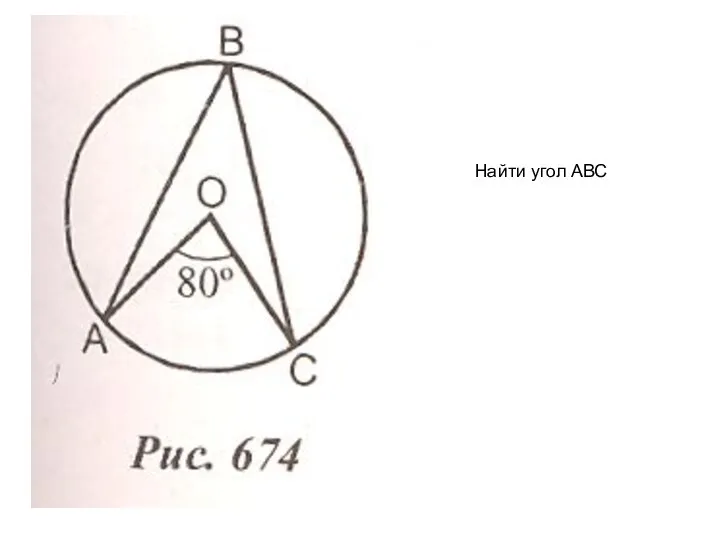 Найти угол АВС
Найти угол АВС Элементы комбинаторики
Элементы комбинаторики Практикум по решению комбинированных уравнений
Практикум по решению комбинированных уравнений Пирамида. Построение правильной треугольной пирамиды
Пирамида. Построение правильной треугольной пирамиды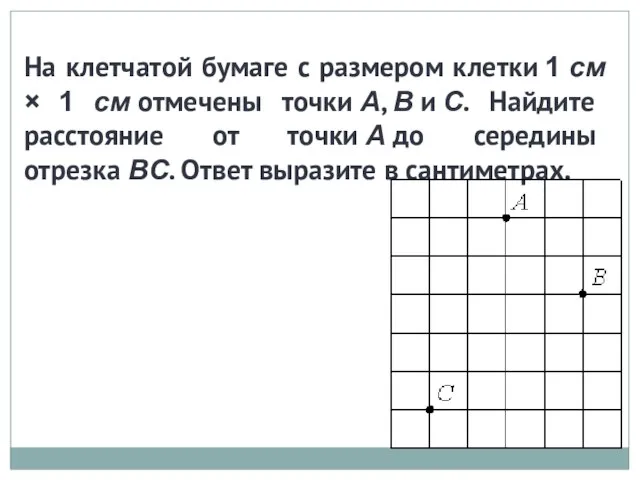 Решение задач
Решение задач МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид
МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид Треугольники. Задача
Треугольники. Задача Приложения скалярного произведения
Приложения скалярного произведения Планы второго порядка
Планы второго порядка Параллелограмм и трапеция
Параллелограмм и трапеция Математика звука
Математика звука Elemente de teoria reziduurilor
Elemente de teoria reziduurilor Многогранники. Тела Архимеда
Многогранники. Тела Архимеда Системы уравнений. Основные понятия
Системы уравнений. Основные понятия Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Решение задач
Решение задач Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі
Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний