Задача дискретного логарифмирования и криптосистемы на ее основе

Задача дискретного логарифмирования

Криптосистемы
протокол Диффи-Хеллмана;
схема Эль-Гамаля;
криптосистема Мэсси-Омуры.

Протокол Диффи-Хеллмана
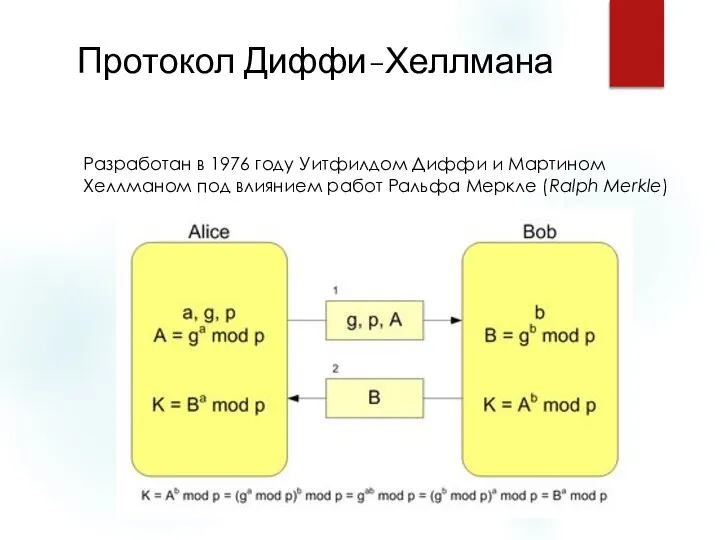
Разработан в 1976 году Уитфилдом Диффи и Мартином Хеллманом под влиянием работ Ральфа Меркле (Ralph Merkle)

Алгоритм

Криптографическая стойкость
Основана на предполагаемой сложности проблемы дискретного логарифмирования.
Работает только на линиях связи, надёжно защищённых от модификации.
Когда в канале возможна модификация данных, появляется очевидная возможность вклинивания в процесс генерации ключей «злоумышленника-посредника» по той же самой схеме, что и для асимметричной криптографии.

Практика
Задание: вычислить открытые ключи A и B, а также общий секретный ключ K, используя открытые параметры g и p и закрытые ключи a и b
Исходные данные
g = 5; p = 23; a = 6; b = 15
К = секретный ключ. К = 2
g = первообразный корень по модулю р. g = 5
A = открытый ключ. A = ga mod p = 8
B = открытый ключ. B = gb mod p = 19