Слайд 2Перед Вами
тема занятия по начертательной геометрии в ряду обычных уроков

или на факультативе в 10-11 математических классах.
Даётся стандартный технический приём, позволяющий решать целый ряд задач. Это внешняя сторона дела.
Слайд 3Суть проблемы:
цель предмета – развитие пространственного мышления . НО большинство учебников

и методик хороши для тех, кто УЖЕ понимает начертательную геометрию.
Строгий язык объяснений лишён образности. Объясняют обычно на плоском чертеже, где не очевидны объём и пространство.
Развитие пространственного мышления подменяют алгоритмом работы с плоской картинкой.
Слайд 4Например, этот правильный чертёж будет восприниматься просто как узор из линий любым
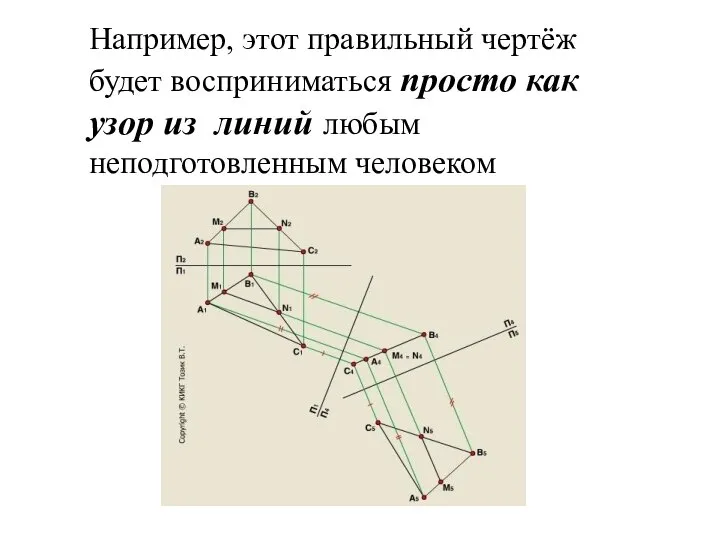
неподготовленным человеком
Слайд 5В предлагаемой здесь методике наглядное (3D)изображение является обязательным.
Плюс для объяснения применяется

сборно-разборный макет-эпюр. Сложил – получил объёмный макет, разложил -- получил плоский чертёж-эпюр.
Сочетание складных макетов с компьютерными 3 D – изображениями помогает действительно понимать плоский чертёж как объём .
Слайд 6Понимают все.
Самостоятельно чертить трудней, чем понимать. Но практически каждый может

научиться. Даже с низкими природными способностями к предмету.
Из опыта: моя выпускница с «природными данными на 2,5 балла» сдала в 2011 году экзамен в ВУЗе на 4 балла.
Слайд 7Тема.
Дополнительная плоскость 2-го порядка.
На примере темы показана суть

предлагаемой методики. Цель её -- развитие пространственного мышления детей.
Построение дополнительных плоскостей -- базовый, часто употребляемый способ преобразования проекций. Способ применяют для получения натуральной величины углов, расстояний и плоских фигур.
Слайд 8 О том же образно.
Дополнительная плоскость проекций подобна экрану для

рентгеновского снимка. Суть дела очень проста -- поставить экран с удобной стороны.
Слайд 9Условие задачи, плоский чертеж, Δ АВС в двух проекциях : на вертикальной
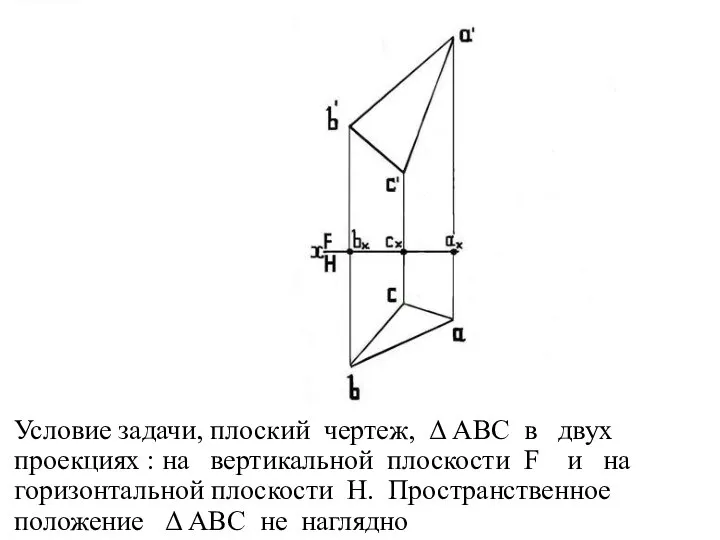
плоскости F и на горизонтальной плоскости H. Пространственное положение Δ АВС не наглядно
Слайд 10Задача -- получить натуральную величину Δ АВС. Для этого надо поставить новый

экран параллельно поверхности треугольника. На параллельном экране Δ изобразится в натуральную величину.
Сначала сделаем задачу наглядной для лучшего её понимания.
Слайд 11Фронтальную проекцию представим рисунком на кирпичной стене, горизонтальную -- рисунком на площадке
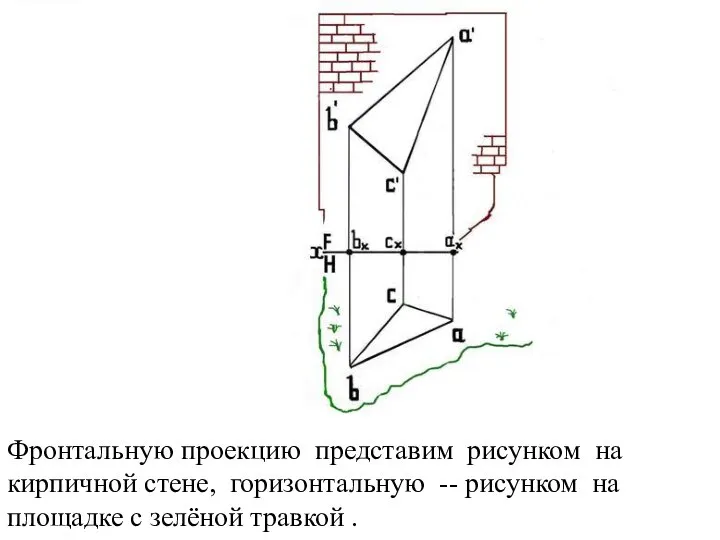
с зелёной травкой .
Слайд 12Представим Δ АВС в виде дощечки , тогда на виде сверху видна
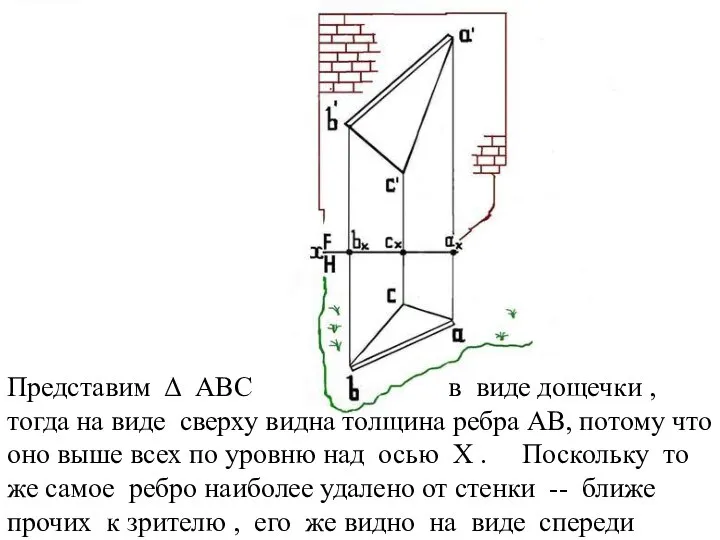
толщина ребра АВ, потому что оно выше всех по уровню над осью Х . Поскольку то же самое ребро наиболее удалено от стенки -- ближе прочих к зрителю , его же видно на виде спереди
Слайд 13 Δ АВС затонирован , теперь его положение в пространстве читается на
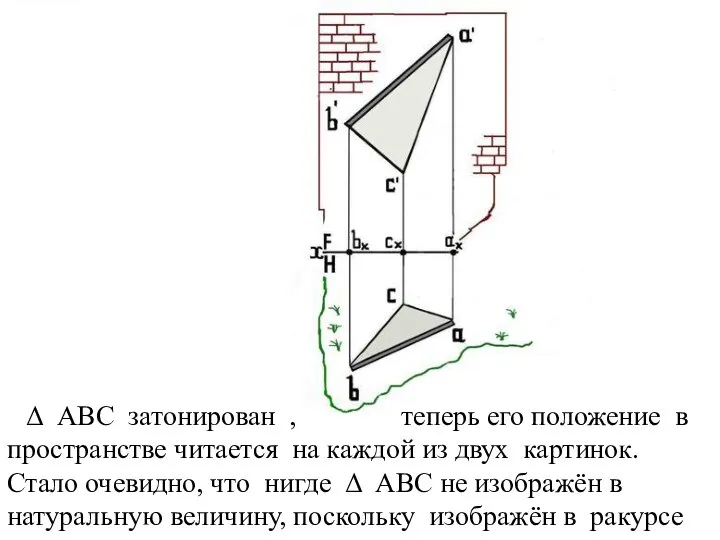
каждой из двух картинок. Стало очевидно, что нигде Δ АВС не изображён в натуральную величину, поскольку изображён в ракурсе
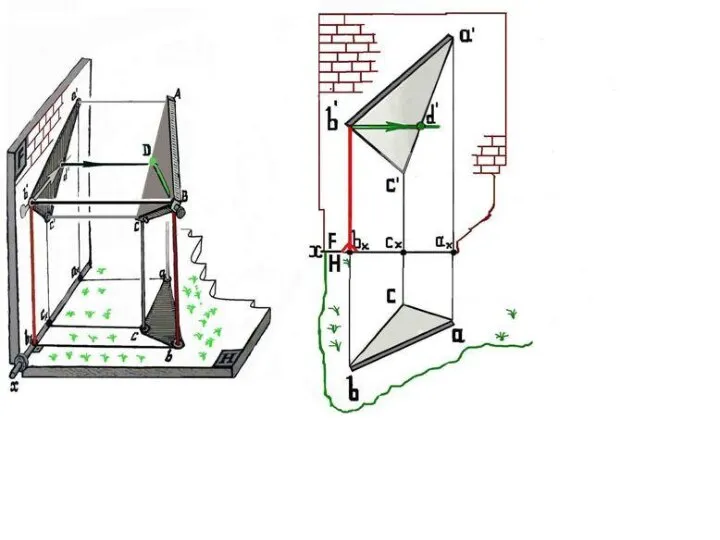
Слайд 14Для полной ясности даны :
справа двухкартинный чертеж -- эпюр (2 D)
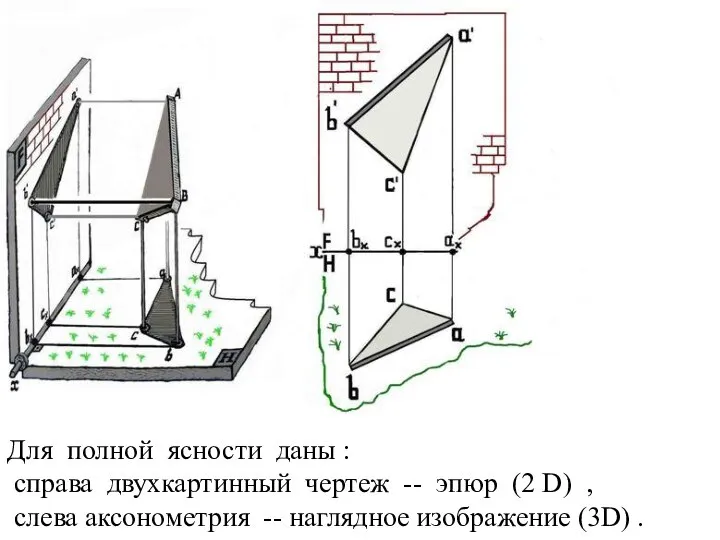
,
слева аксонометрия -- наглядное изображение (3D) .
Слайд 22Горизонталь BD – зелёный гвоздь -- на горизонтальном экране имеет натуральную величину
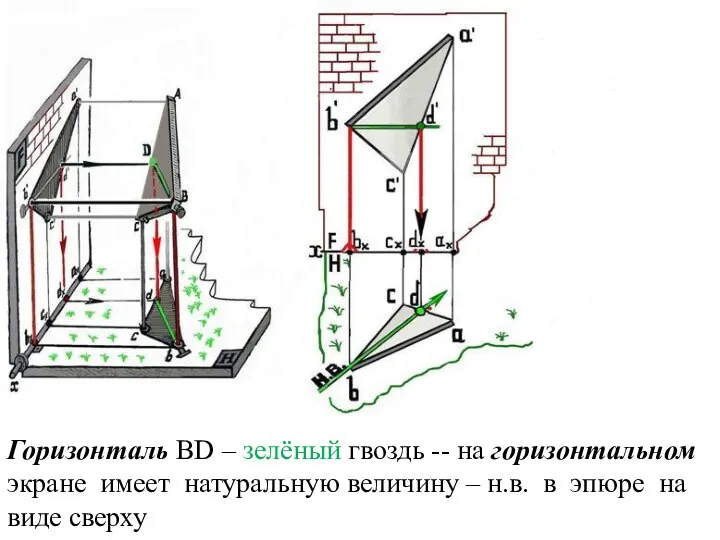
– н.в. в эпюре на виде сверху
Слайд 23Чтобы быть ┴ треугольнику, должна быть ┴ его горизонтали новая вертикальная стена.
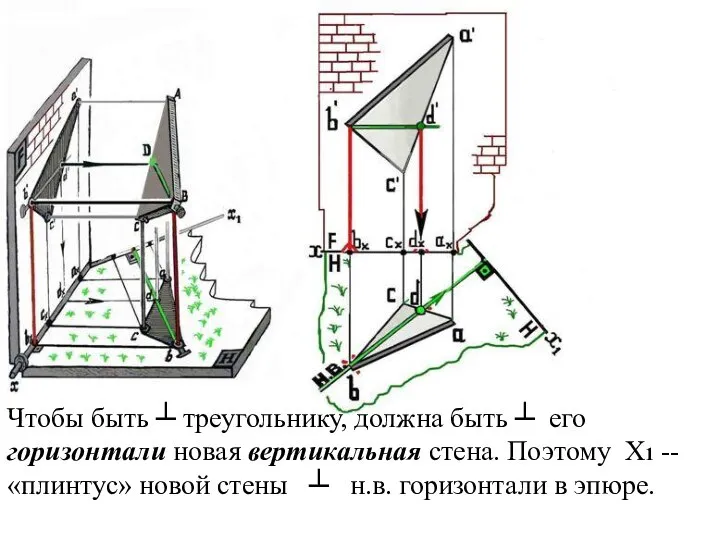
Поэтому X1 -- «плинтус» новой стены ┴ н.в. горизонтали в эпюре.
Слайд 24Создаём новый экран -- стенку F1 , то есть дополнительную плоскость проекций
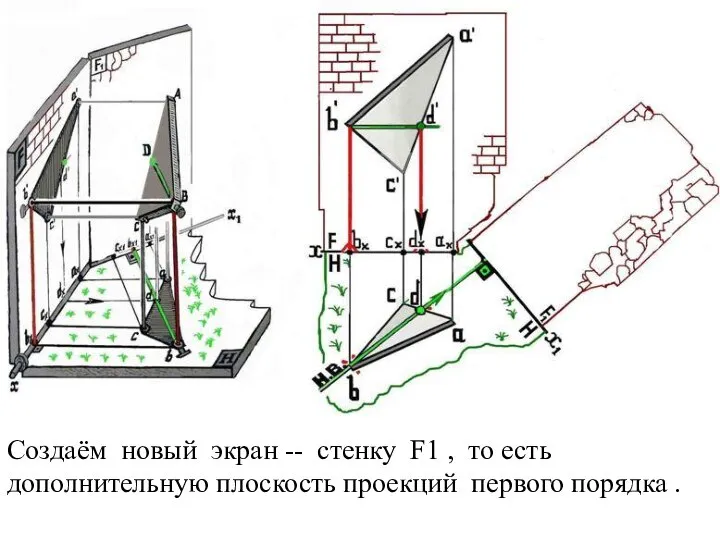
первого порядка .
Слайд 25Начинаем проецировать ┴ плоскости F1 ,
то есть начинаем «вбивать» зелёный гвоздь
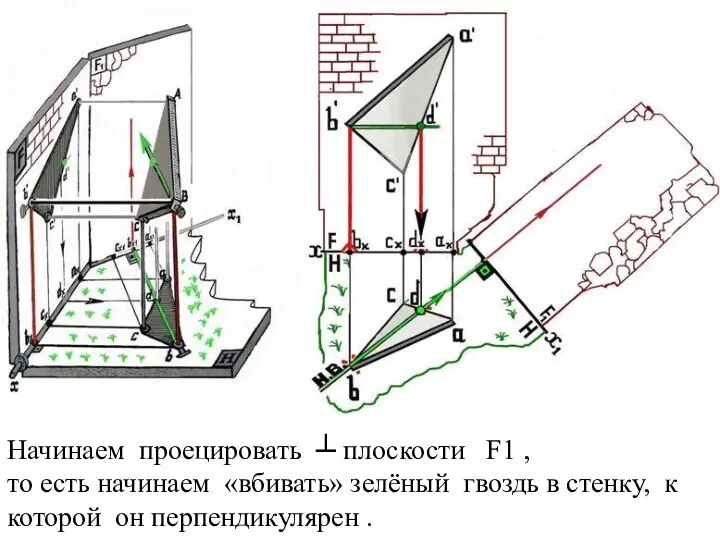
в стенку, к которой он перпендикулярен .
Слайд 26На обеих красных стенках «красненькое = красненькому » -- высоты = высотам
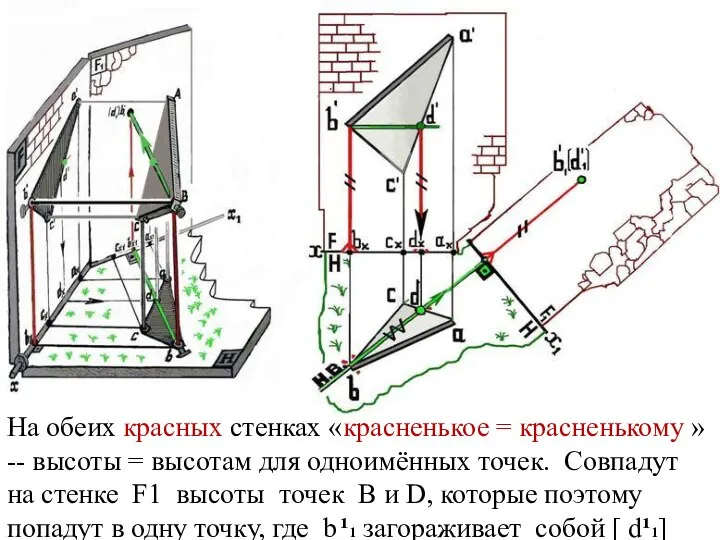
для одноимённых точек. Совпадут на стенке F1 высоты точек В и D, которые поэтому попадут в одну точку, где b ¹1 загораживает собой [ d¹1]
Слайд 27На обеих стенках высоты равны высотам для одноимённых точек.
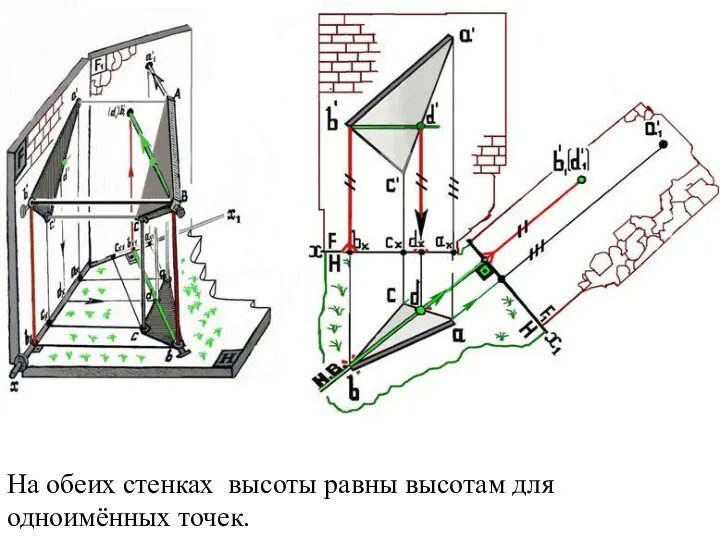
Слайд 28Каждый гвоздь проходит в «теле» плоскости АВС и «превращается» в точку на
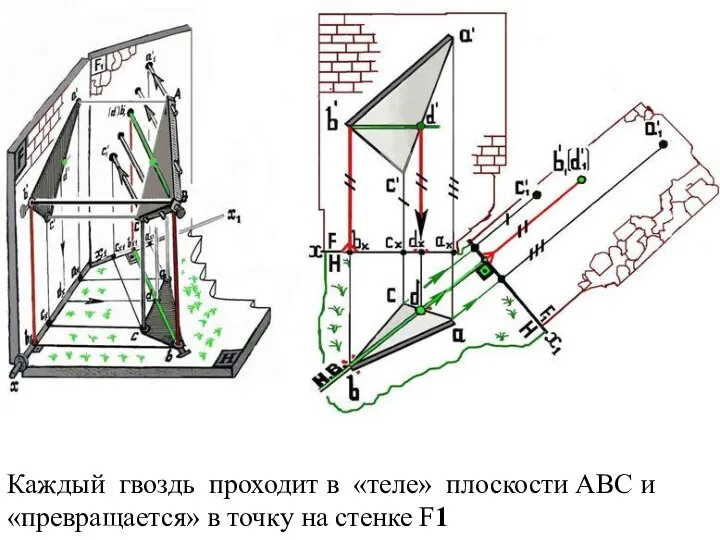
стенке F1
Слайд 29Поскольку каждый гвоздь проходит в «теле» плоскости АВС и «превращается» в точку
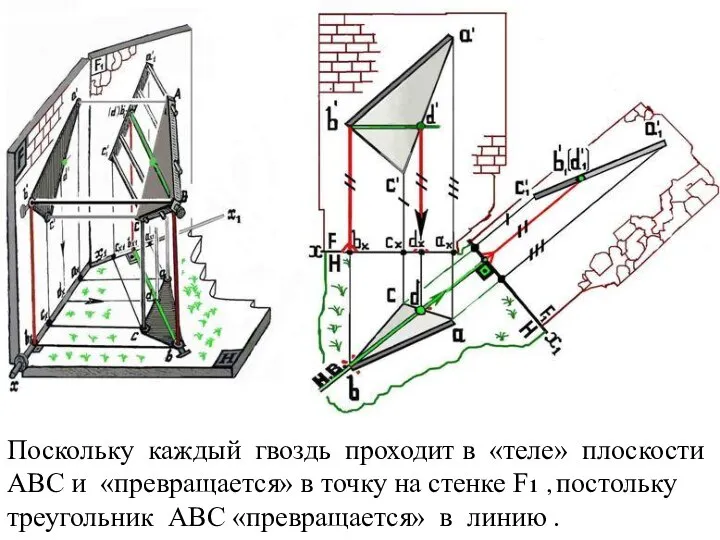
на стенке F1 , постольку треугольник АВС «превращается» в линию .
Слайд 30Новое направление лучей будет перпендикулярно плоскости АВС , поэтому перпендикулярно линии, в
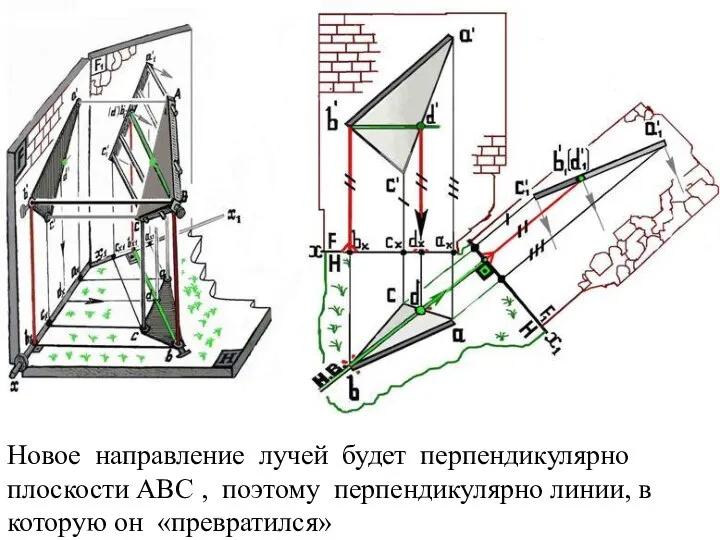
которую он «превратился»
Слайд 31 Параллельно линии , в которую «превратился » треугольник АВС , строим
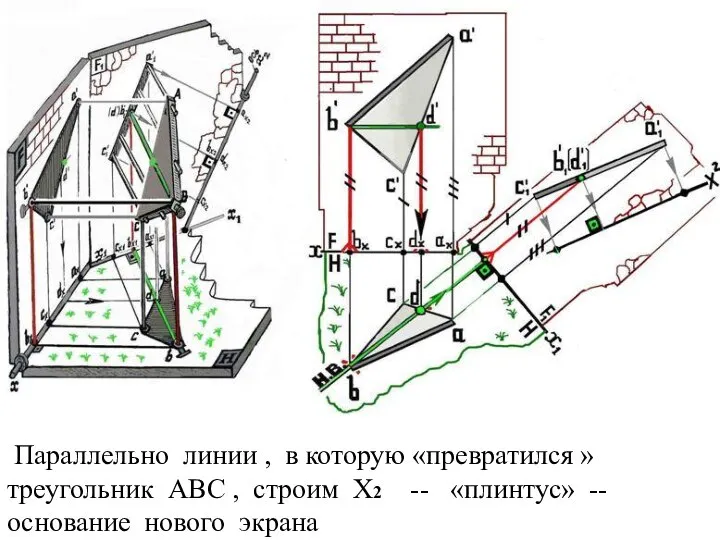
Х2 -- «плинтус» -- основание нового экрана
Слайд 32Построен экран Н1 перпендикулярно F1 .
Н1 -- это в сущности наклонный
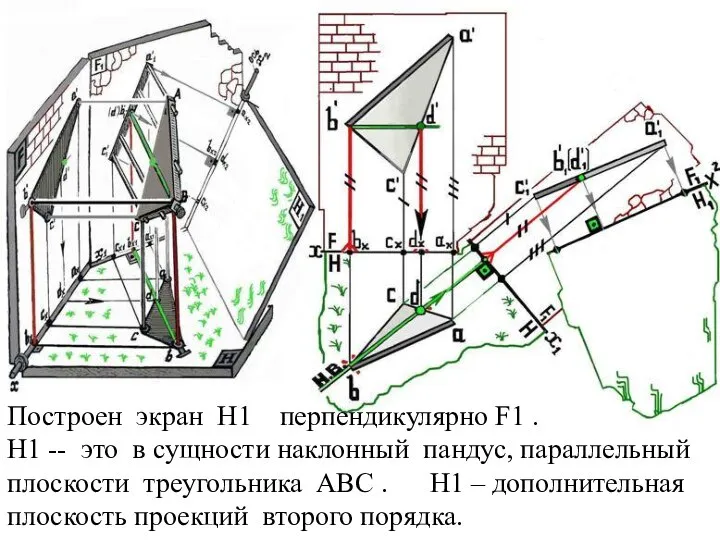
пандус, параллельный плоскости треугольника АВС . Н1 – дополнительная плоскость проекций второго порядка.
Слайд 33Начинаем проецировать на экран Н1 , параллельный треугольнику АВС
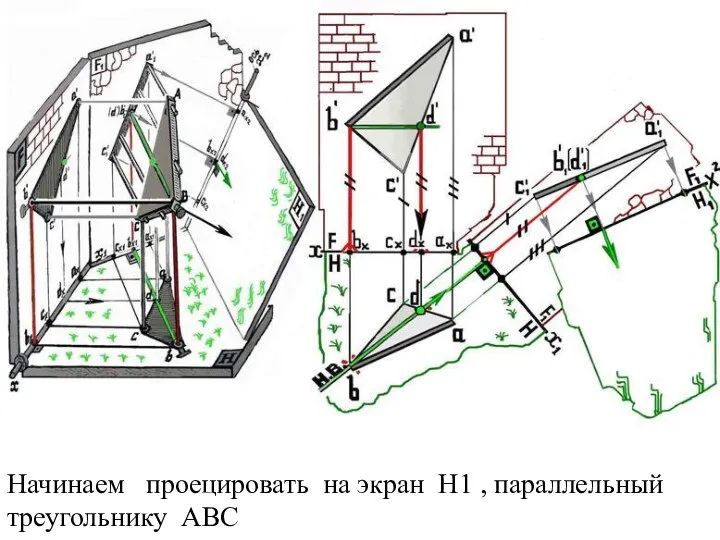
Слайд 34Зелёненькое равно зелёненькому -- то есть вдоль зелёной травки расстояние от стенки
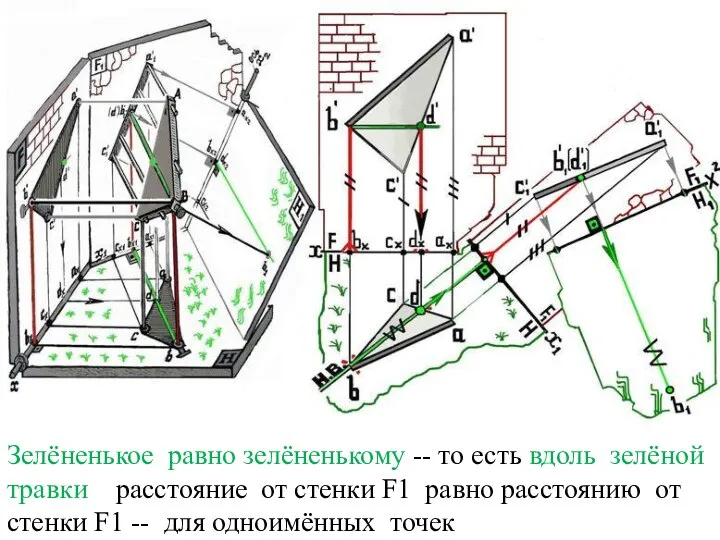
F1 равно расстоянию от стенки F1 -- для одноимённых точек
Слайд 35Зелёненькое равно зелёненькому -- расстояние от стенки F1 равно расстоянию от стенки
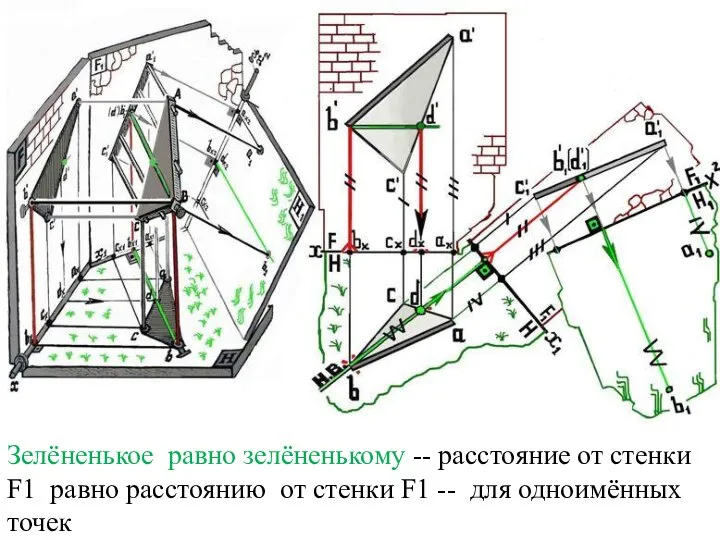
F1 -- для одноимённых точек
Слайд 36Зелёненькое равно зелёненькому -- расстояние от стенки F1 равно расстоянию от стенки
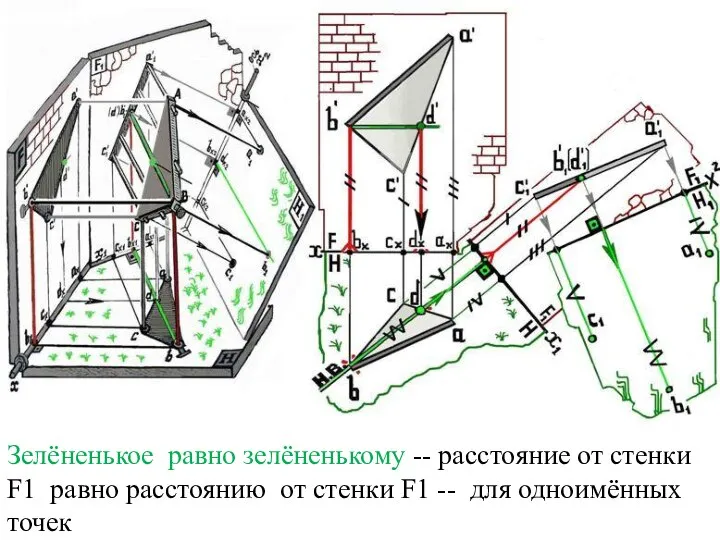
F1 -- для одноимённых точек
Слайд 37Зелёненькое равно зелёненькому -- расстояние от стенки F1 равно расстоянию от стенки
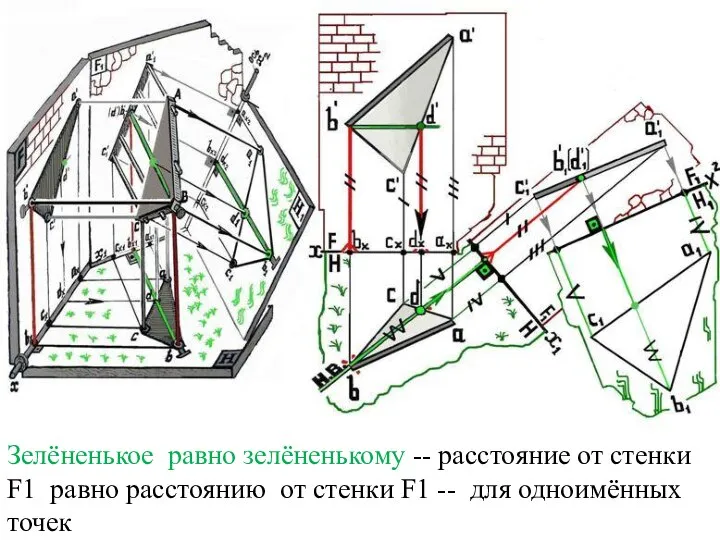
F1 -- для одноимённых точек
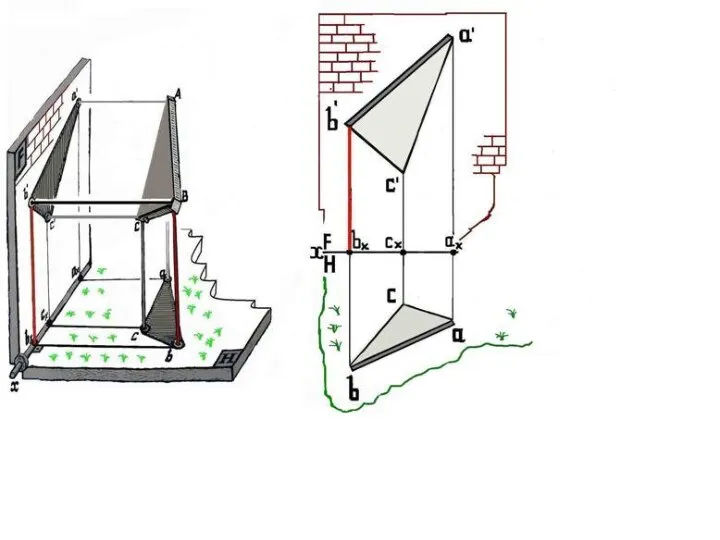
Слайд 38Условие задачи, плоский чертеж.
Треугольник АВС на двух экранах, на фронтальной
Треугольник а1
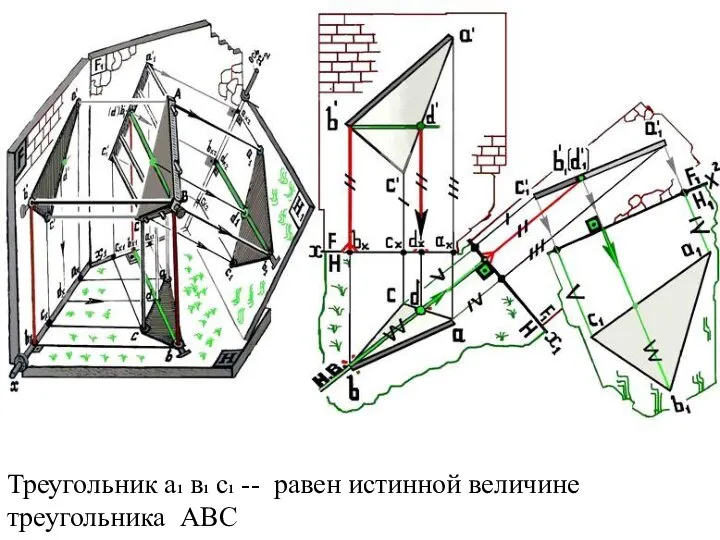
в1 с1 -- равен истинной величине треугольника АВС



































 Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Векторная алгебра
Векторная алгебра Презентация на тему Формулы (5 класс)
Презентация на тему Формулы (5 класс)  Презентация на тему Исследование функции с помощью производной
Презентация на тему Исследование функции с помощью производной  Аксиомы стереометрии
Аксиомы стереометрии Оператор Лапласа в полярных, цилиндрических и сферических системах координат
Оператор Лапласа в полярных, цилиндрических и сферических системах координат Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Виды четырехугольников
Виды четырехугольников Цилиндр
Цилиндр Симметрия вокруг нас
Симметрия вокруг нас Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Метод координат в пространстве
Метод координат в пространстве Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Состав числа 8
Состав числа 8 Учимся писать цифры
Учимся писать цифры Длина окружности и число пи
Длина окружности и число пи Геометрия, как наука
Геометрия, как наука Чётные и нечётные числа. Подготовка к контрольной работе
Чётные и нечётные числа. Подготовка к контрольной работе Многозначная логика
Многозначная логика Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Вычислительная математика. Практика №1
Вычислительная математика. Практика №1 Координатная плоскость. Графики
Координатная плоскость. Графики Уравнение прямой
Уравнение прямой Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Теорема Фалеса
Теорема Фалеса Решение уравнений. Тест
Решение уравнений. Тест Методы многокритериальной оптимизации
Методы многокритериальной оптимизации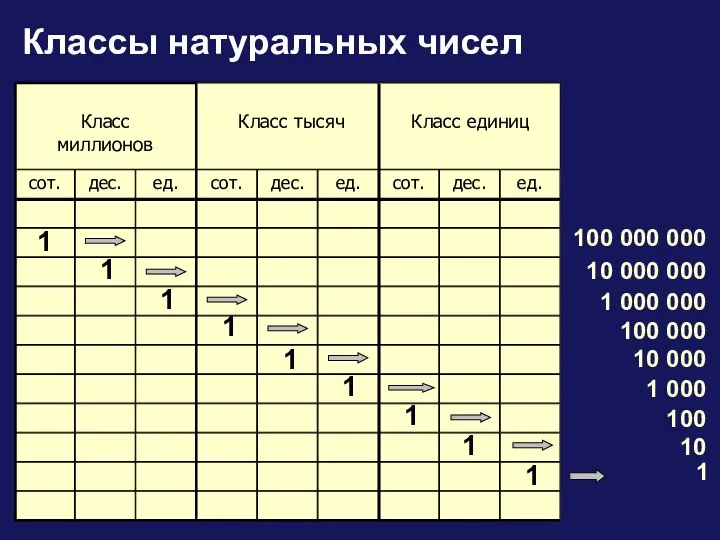 Классы натуральных чисел
Классы натуральных чисел