Пример записи решения задания к Части I РГР №1

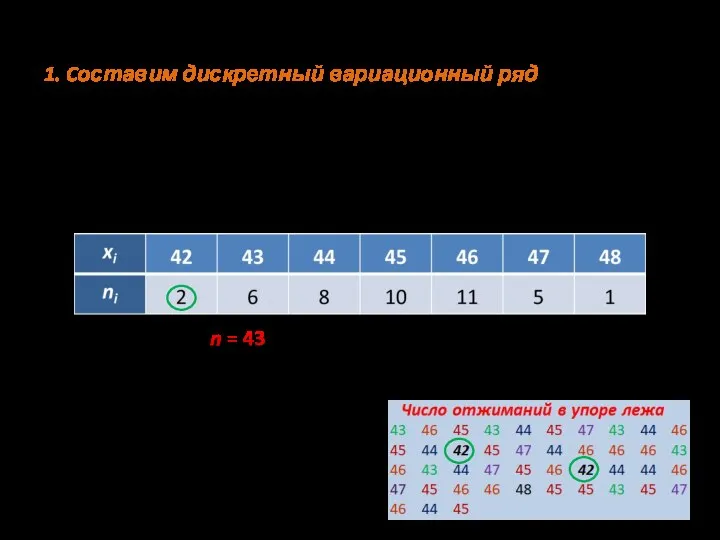
Этапы выполнения:
1. Cоставим дискретный вариационный ряд
Все варианты расположим в порядке возрастания в первой строке таблицы, а частоту, с которой они встречаются в данной выборке – во второй строке.
Для облегчения определения частоты выделим одинаковые значения одним цветом.
Объем выборки n = 43.
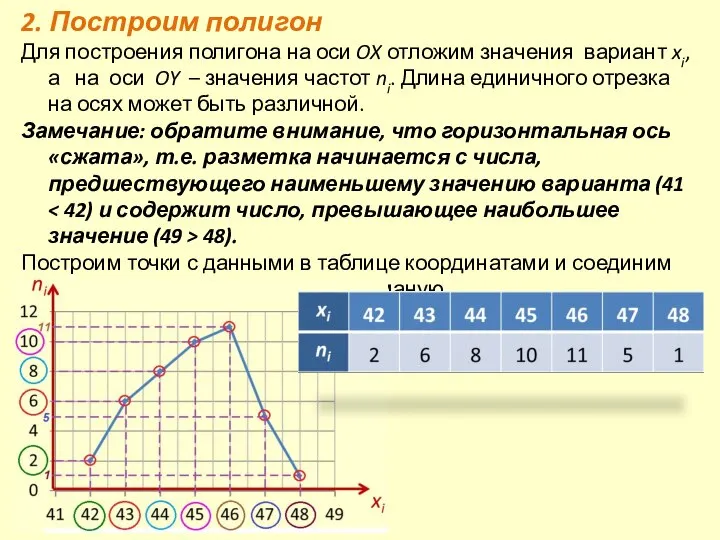
Контроль: n = 2 + 6 + 8 + 10 + 11 + 5 + 1 = 43

2. Построим полигон
Для построения полигона на оси OX отложим значения вариант xi, а на оси OY – значения частот ni. Длина единичного отрезка на осях может быть различной.
Замечание: обратите внимание, что горизонтальная ось «сжата», т.е. разметка начинается с числа, предшествующего наименьшему значению варианта (41 < 42) и содержит число, превышающее наибольшее значение (49 > 48).
Построим точки с данными в таблице координатами и соединим их последовательно, получив ломаную.

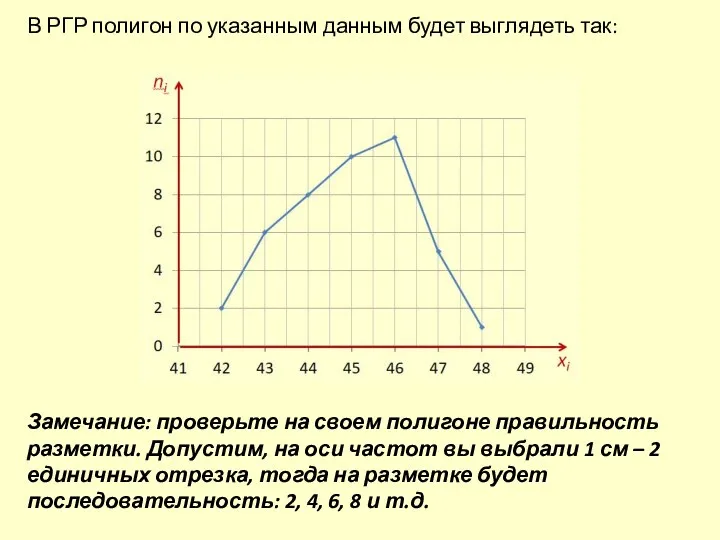
В РГР полигон по указанным данным будет выглядеть так:
Замечание: проверьте на своем полигоне правильность разметки. Допустим, на оси частот вы выбрали 1 см – 2 единичных отрезка, тогда на разметке будет последовательность: 2, 4, 6, 8 и т.д.

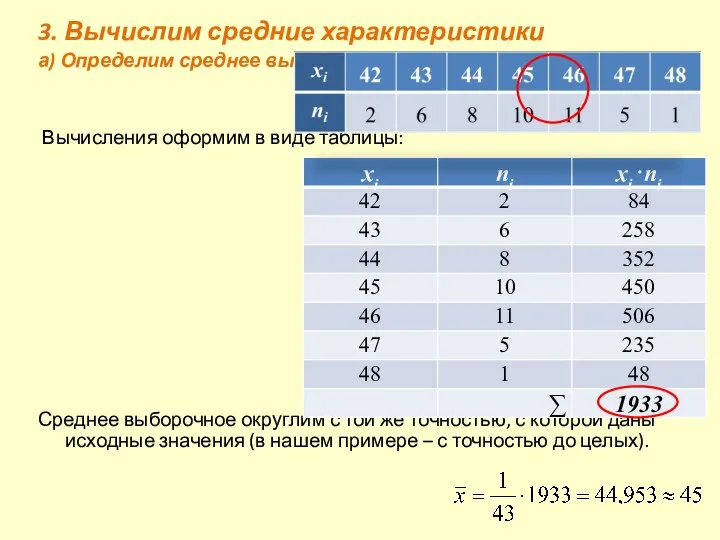
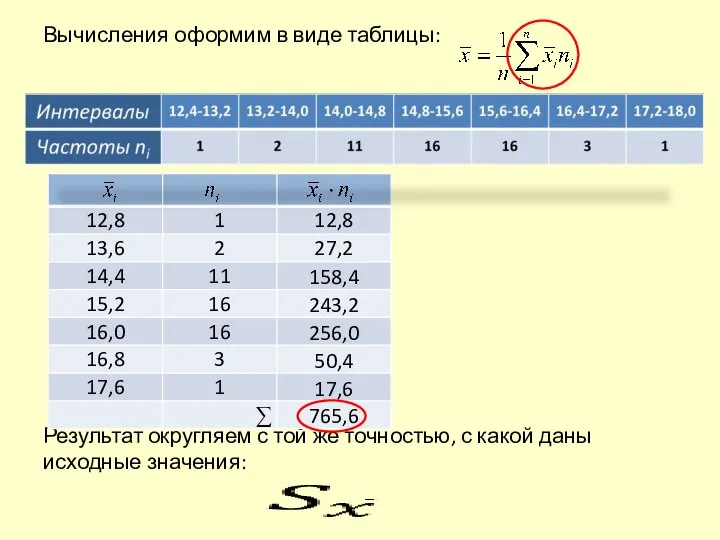
3. Вычислим средние характеристики
а) Определим среднее выборочное:
Вычисления оформим в виде таблицы:
Среднее выборочное округлим с той же точностью, с которой даны исходные значения (в нашем примере – с точностью до целых).

б) Определим моду:
В данном примере наибольшая частота – 11. Она соответствует значению xi = 46.
Замечание:
Если два соседних значения имеют наибольшую частоту, то мода – их среднее арифметическое (не забудьте округлить результат с той же точностью, что и исходные значения).
Если они не соседние, то ряд бимодальный (то есть имеет 2 моды).
Если таких значений больше двух, то ряд моды не имеет.

в) Определим медиану :
Выборку сначала необходимо проранжировать (расположить значения по возрастанию):
42 43 43 43 43 43 43 44 44
44 44 44 44 44 44 45 45 45 45
45 45 45 45 45 46 46 46 46
46 46 46 46 46 46 47 47 47
47 47 48
Объем выборки n = 43 является нечетным числом,
следовательно , где .
Значит, , то есть
22-ой по счету вариант в ранжированном ряду и будет медианой:

4. Вычислим характеристики вариации
а) Определим размах вариации :

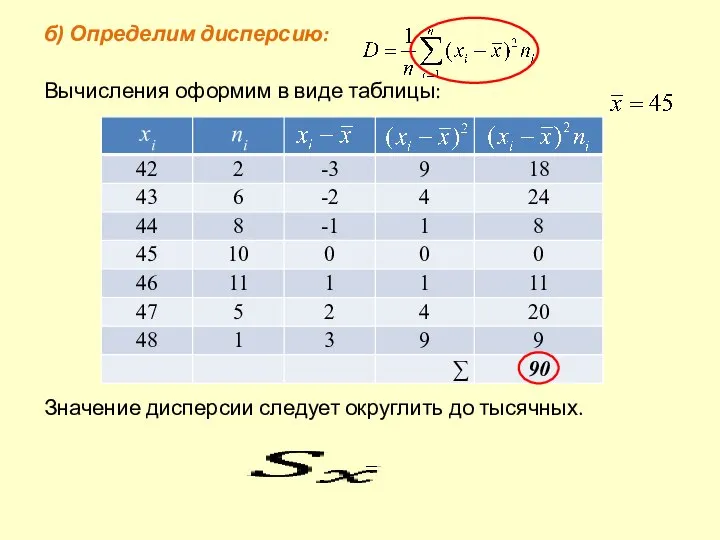
б) Определим дисперсию:
Вычисления оформим в виде таблицы:
Значение дисперсии следует округлить до тысячных.
xi
ni

в) Определим среднее квадратическое отклонение:
Для использования в дальнейших расчетах значение округляется до тысячных, но для интерпретации в выводе округление производят с той же точностью, что и исходные значения (в нашем примере – округление до целых).
Для дальнейших расчетов:
Для интерпретации в выводе:

г) Определим коэффициент вариации:
Коэффициент вариации округляют до десятых долей процента, чтобы правильно оценить однородность выборки.

д) Определим ошибку выборочного среднего:

5. Вывод. По данным числа отжиманий в упоре лежа 43 испытуемых средний результат составил 45 раз ± 0 раз. Степень рассеяния данных выборки от среднего результата составляет 1 отжимание. Чаще всего встречаемый результат в группе – 46 отжиманий. Одна половина спортсменов показала результаты лучше 45 отжиманий, а другая половина хуже. Отклонение результатов числа отжиманий в упоре лежа внутри группы равно 6 отжиманиям. Результаты исследования имеют малую варьируемость, что говорит об однородности выборки, то есть средний результат типичен для изучаемого признака.
n
σ

ПРИМЕР ЗАПИСИ РЕШЕНИЯ ЗАДАНИЯ
К ЧАСТИ II РГР №1
Задание: По данным выборки:
1. Составить интервальный вариационный ряд.
2. Построить гистограмму.
3. Найти средние характеристики:
а) среднее выборочное ;
б) моду Mo;
в) медиану Me.
4. Найти характеристики вариации:
а) размах вариации XR ;
б) дисперсию D;
в) среднее квадратическое отклонение σ;
г) коэффициент вариации V;
д) ошибку выборочного среднего .
5. Сделать вывод.
Исходные данные:
Бег на 100 м (юноши 9 классов)
16,2 15,5 14,3 16,6 15,8 15,4 14,5 14,8 16,1 15,8
15,3 16,0 13,7 16,1 16,2 15,3 15,5 14,8 14,3 16,2
15,3 15,8 14,2 15,8 14,2 15,4 14,7 12,8 16,9 15,0
16,8 16,0 14,6 15,6 16,1 17,8 15,6 15,0 15,6 15,0
16,2 15,5 13,6 16,4 15,2 15,9 15,0 14,2 16,4 14,2

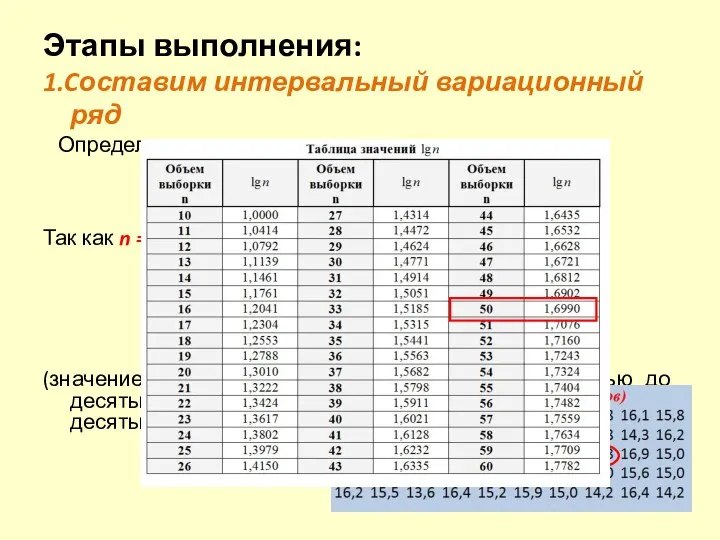
Этапы выполнения:
1.Cоставим интервальный вариационный ряд
Определим величину интервала:
Так как n = 50, определим значения lg 50, xmax и xmin .
lg 50 = 1,6990, xmax = 17,8, xmin = 12,8
(значение величины интервала округляем с точностью до десятых, так как исходные данные имеют точность до десятых долей).

Найдем границы интервалов. Округление производить не надо.
Левой границей первого интервала будет число:
Вычисляем далее до тех пор, пока полученное значение не станет равным или не превысит xmax.

Определяем количество значений, которые входят в указанные интервалы.
Замечание: если число совпадает с границей интервала, то считается, что оно включено в тот интервал, для которого является правой границей. Например, число 14,0 будет включено во второй интервал 13,2-14,0, и не будет входить в интервал 14,0-14,8.
Результаты оформляем в виде таблицы:
Объем выборки n = 50.
Контроль: n = 1 + 2 + 11 + 16 + 16 + 3 + 1 = 50

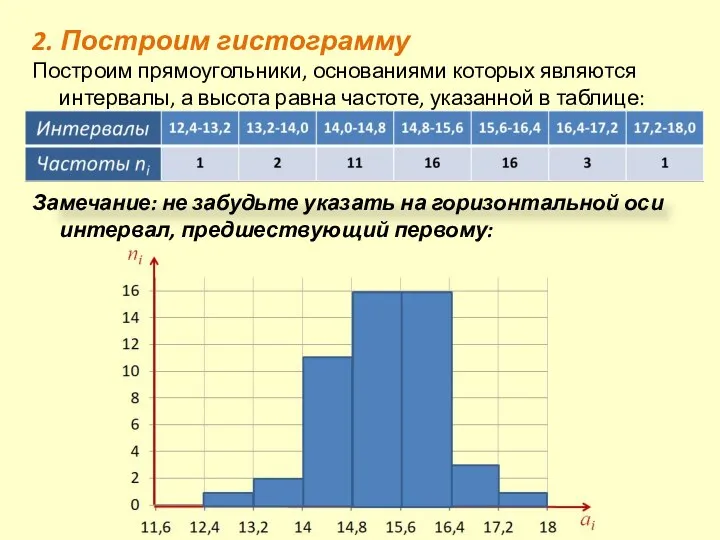
2. Построим гистограмму
Построим прямоугольники, основаниями которых являются интервалы, а высота равна частоте, указанной в таблице:
Замечание: не забудьте указать на горизонтальной оси интервал, предшествующий первому:

Вычисления оформим в виде таблицы:
Результат округляем с той же точностью, с какой даны исходные значения:

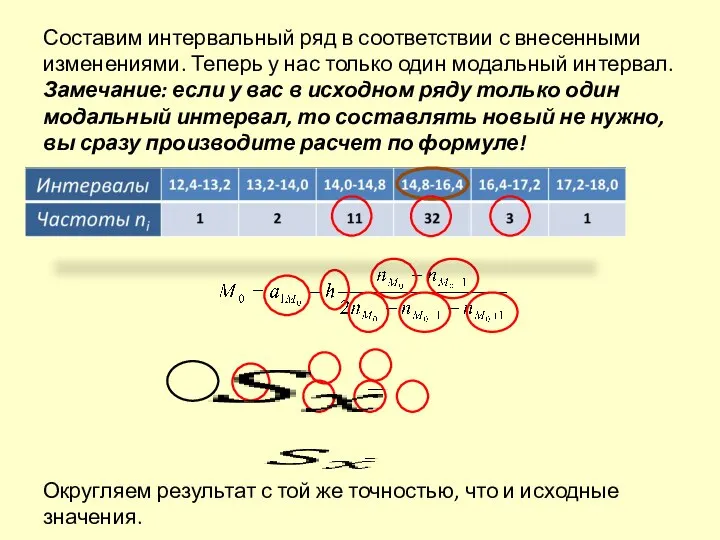
б) Определим моду:
Определим модальный интервал – тот, для которого частота принимает наибольшее значение.
Замечание: если таких интервалов 2, и они не соседние, то производится расчет для каждого отдельно, и ряд имеет 2 моды.
В данном примере рассматривается сложный случай: 2 соседних интервала имеют одинаковую наибольшую частоту. В этом случае они объединяются и рассматриваются как один интервал с границами 14,8-16,4.
Длина интервала h = 16,4 – 14,8 = 1,6.
Его частота ni = 16 + 16 = 32.

Составим интервальный ряд в соответствии с внесенными изменениями. Теперь у нас только один модальный интервал.
Замечание: если у вас в исходном ряду только один модальный интервал, то составлять новый не нужно, вы сразу производите расчет по формуле!
Округляем результат с той же точностью, что и исходные значения.

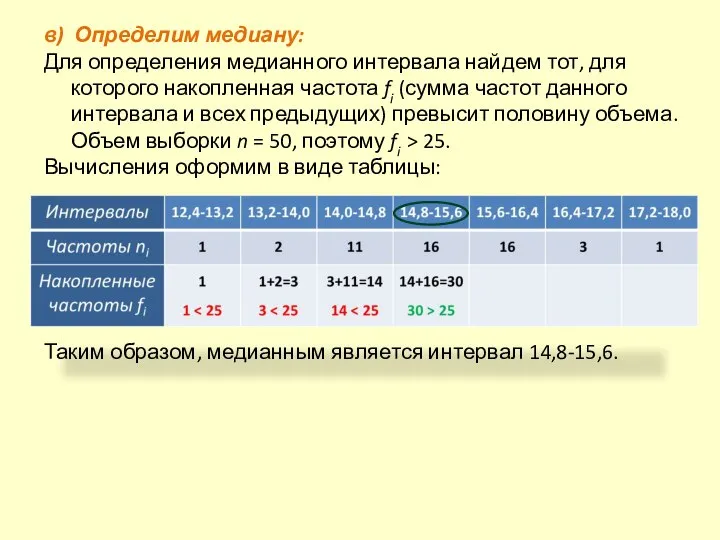
в) Определим медиану:
Для определения медианного интервала найдем тот, для которого накопленная частота fi (сумма частот данного интервала и всех предыдущих) превысит половину объема. Объем выборки n = 50, поэтому fi > 25.
Вычисления оформим в виде таблицы:
Таким образом, медианным является интервал 14,8-15,6.

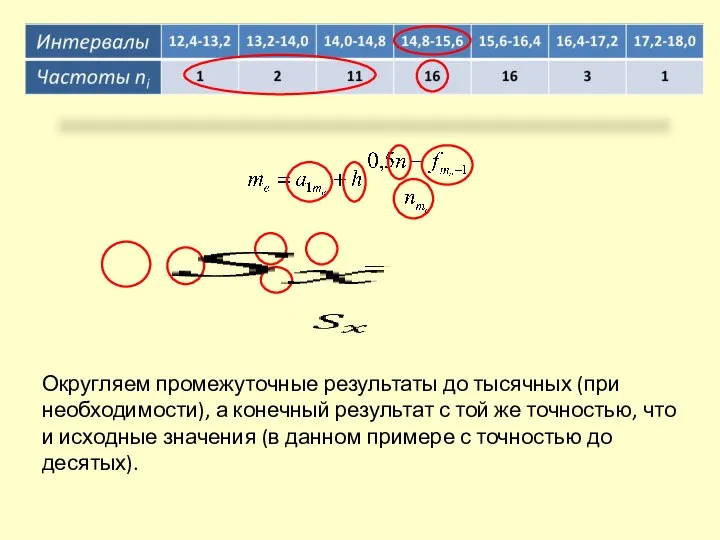
Округляем промежуточные результаты до тысячных (при необходимости), а конечный результат с той же точностью, что и исходные значения (в данном примере с точностью до десятых).

4. Вычислим характеристики вариации
а) Определим размах вариации :

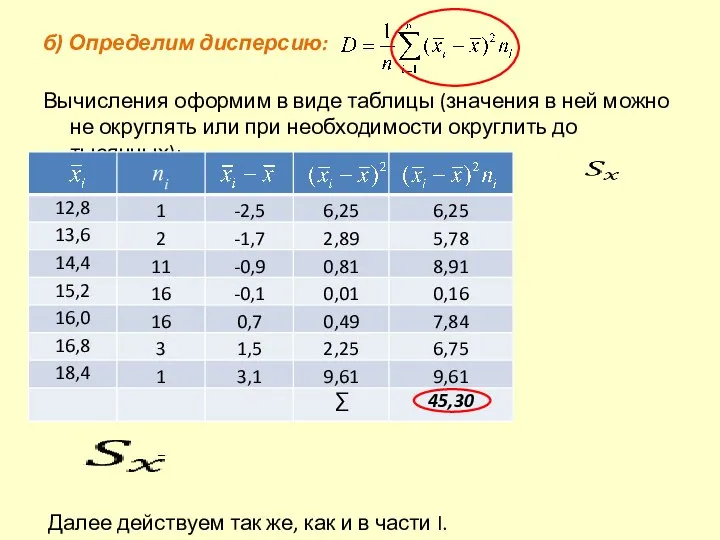
б) Определим дисперсию:
Вычисления оформим в виде таблицы (значения в ней можно не округлять или при необходимости округлить до тысячных):
Далее действуем так же, как и в части I.
ni

в) Определим среднее квадратическое отклонение:
Для использования в дальнейших расчетах значение округляется до тысячных, но для интерпретации в выводе округление производят с той же точностью, что и исходные значения (в нашем примере – округление до десятых).
Для дальнейших расчетов:
Для интерпретации в выводе:

г) Определим коэффициент вариации:
Коэффициент вариации округляют до десятых долей процента, чтобы правильно оценить однородность выборки.

д) Определим ошибку выборочного среднего: