Призма. Пирамида

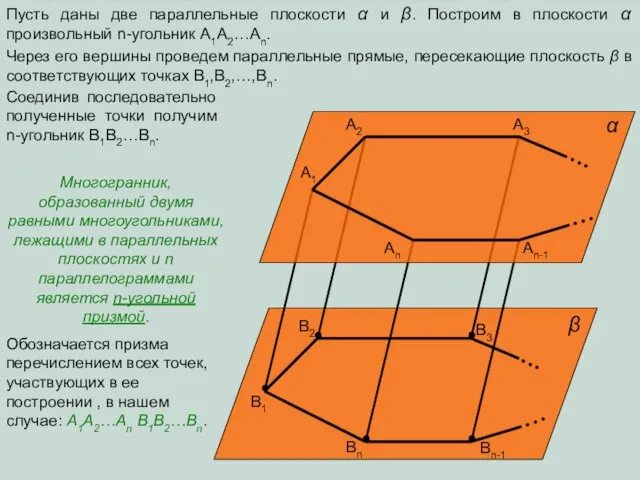
Пусть даны две параллельные плоскости α и β. Построим в плоскости α произвольный n-угольник A1A2…An.
A1
A2
A3
An
An-1
α
β
B1
B2
B3
Bn
Bn-1
Через его вершины проведем параллельные прямые, пересекающие плоскость β в соответствующих точках В1,В2,…,Вn.
Соединив последовательно полученные точки получим n-угольник B1B2…Bn.
Многогранник, образованный двумя равными многоугольниками, лежащими в параллельных плоскостях и n параллелограммами является n-угольной призмой.
Обозначается призма перечислением всех точек, участвующих в ее построении , в нашем случае: A1A2…An B1B2…Bn.

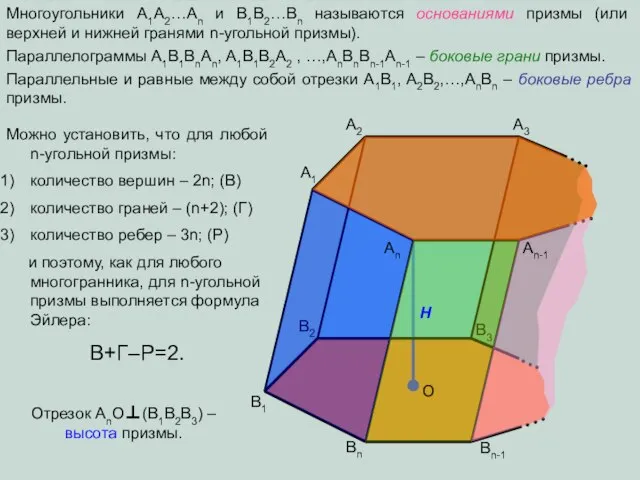
A1
A2
A3
B1
B2
B3
Bn
Bn-1
Многоугольники A1A2…An и В1В2…Вn называются основаниями призмы (или верхней и нижней гранями n-угольной призмы).
Параллелограммы A1B1BnAn, A1B1B2A2 , …,AnBnBn-1An-1 – боковые грани призмы.
Параллельные и равные между собой отрезки A1B1, A2B2,…,AnBn – боковые ребра призмы.
Можно установить, что для любой n-угольной призмы:
количество вершин – 2n; (В)
количество граней – (n+2); (Г)
количество ребер – 3n; (Р)
и поэтому, как для любого многогранника, для n-угольной призмы выполняется формула Эйлера:
В+Г–Р=2.
An
An-1
H
O
Отрезок AnO⊥(B1B2B3) – высота призмы.

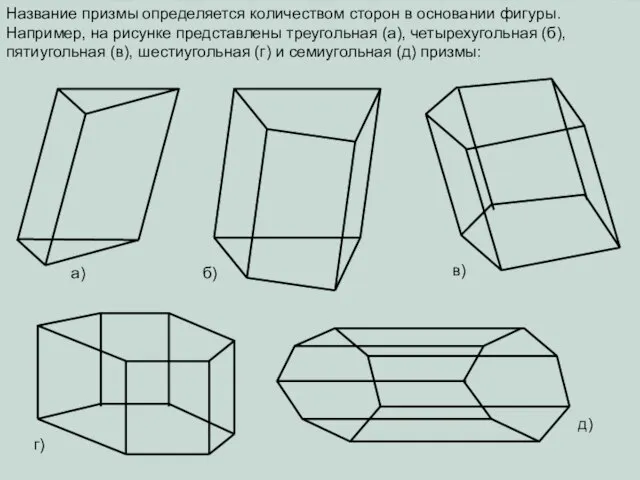
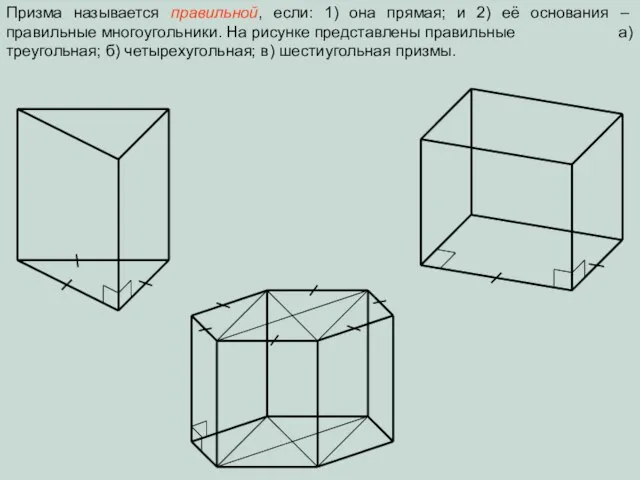
Название призмы определяется количеством сторон в основании фигуры. Например, на рисунке представлены треугольная (а), четырехугольная (б), пятиугольная (в), шестиугольная (г) и семиугольная (д) призмы:
а)
б)
в)
г)
д)

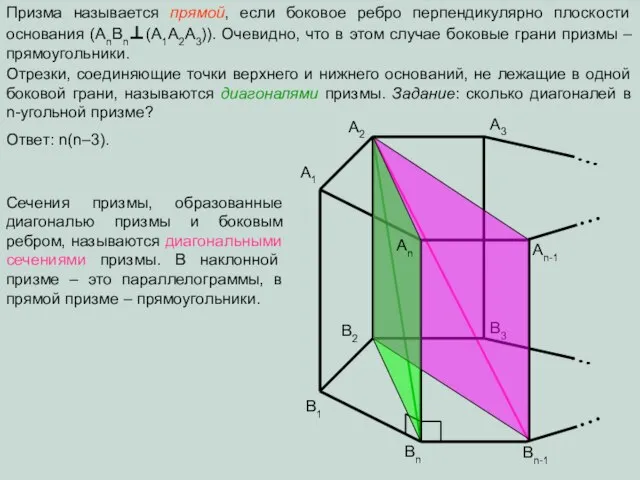
Призма называется прямой, если боковое ребро перпендикулярно плоскости основания (AnBn⊥(A1A2A3)). Очевидно, что в этом случае боковые грани призмы – прямоугольники.
Отрезки, соединяющие точки верхнего и нижнего оснований, не лежащие в одной боковой грани, называются диагоналями призмы. Задание: сколько диагоналей в n-угольной призме?
A1
A2
A3
An-1
B1
B2
B3
Bn
Bn-1
Ответ: n(n–3).
Сечения призмы, образованные диагональю призмы и боковым ребром, называются диагональными сечениями призмы. В наклонной призме – это параллелограммы, в прямой призме – прямоугольники.
An

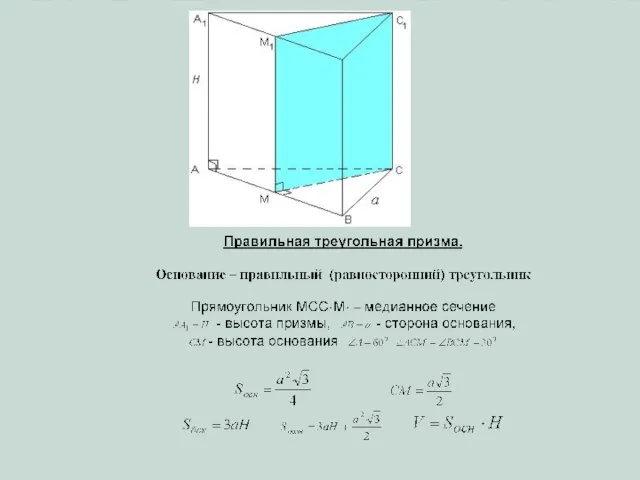
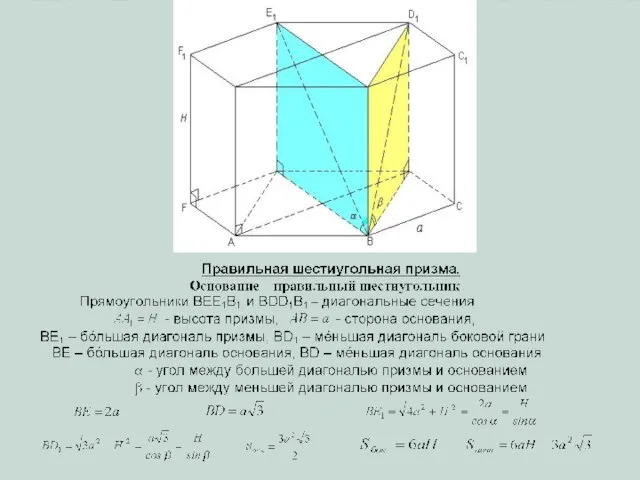
Призма называется правильной, если: 1) она прямая; и 2) её основания – правильные многоугольники. На рисунке представлены правильные а) треугольная; б) четырехугольная; в) шестиугольная призмы.

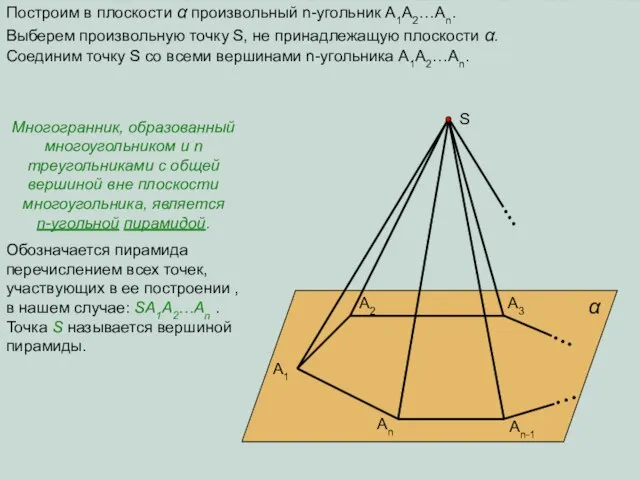
A1
A2
A3
An
An-1
α
Построим в плоскости α произвольный n-угольник A1A2…An.
Выберем произвольную точку S, не принадлежащую плоскости α.
S
Соединим точку S со всеми вершинами n-угольника A1A2…An.
Многогранник, образованный многоугольником и n треугольниками с общей вершиной вне плоскости многоугольника, является n-угольной пирамидой.
Обозначается пирамида перечислением всех точек, участвующих в ее построении , в нашем случае: SA1A2…An . Точка S называется вершиной пирамиды.

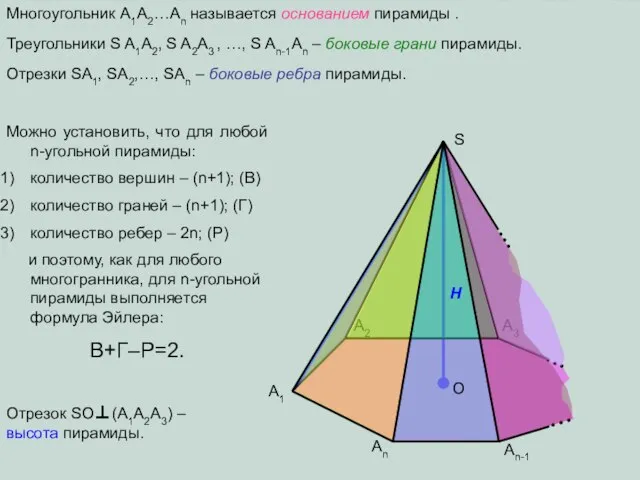
A1
A2
A3
An
An-1
S
Многоугольник A1A2…An называется основанием пирамиды .
Треугольники S A1A2, S A2A3 , …, S An-1An – боковые грани пирамиды.
Отрезки SA1, SA2,…, SAn – боковые ребра пирамиды.
Можно установить, что для любой n-угольной пирамиды:
количество вершин – (n+1); (В)
количество граней – (n+1); (Г)
количество ребер – 2n; (Р)
и поэтому, как для любого многогранника, для n-угольной пирамиды выполняется формула Эйлера:
В+Г–Р=2.
H
O
Отрезок SO⊥(A1A2A3) – высота пирамиды.

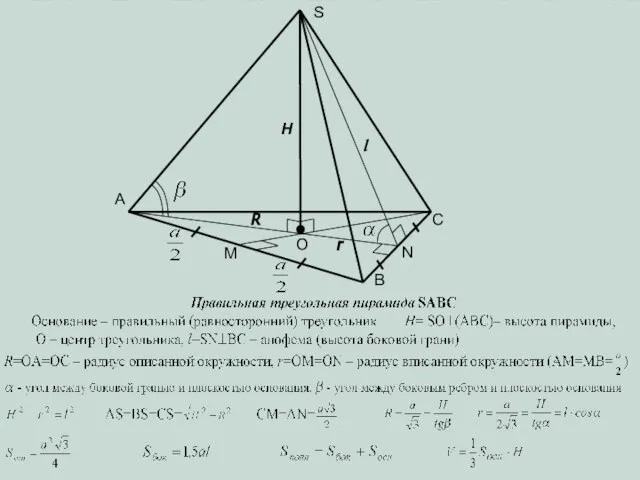
A
B
N
O
M
S
H
R
l
r
C

A
C
D
O
M
S
H
R
l
r