Признак перпендикулярности двух плоскостей

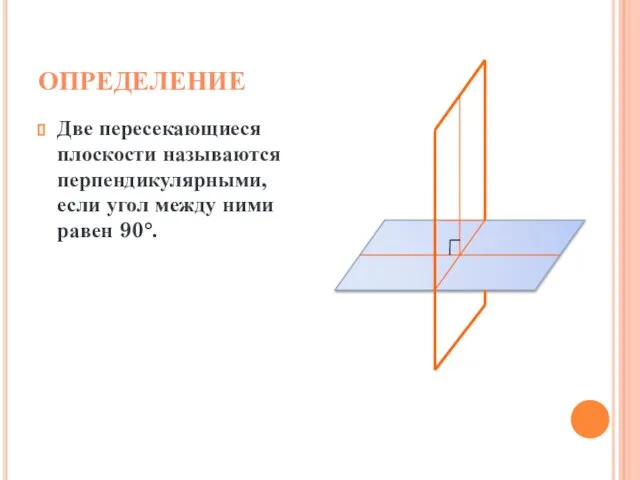
ОПРЕДЕЛЕНИЕ
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90°.

ПРИМЕР
Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты.

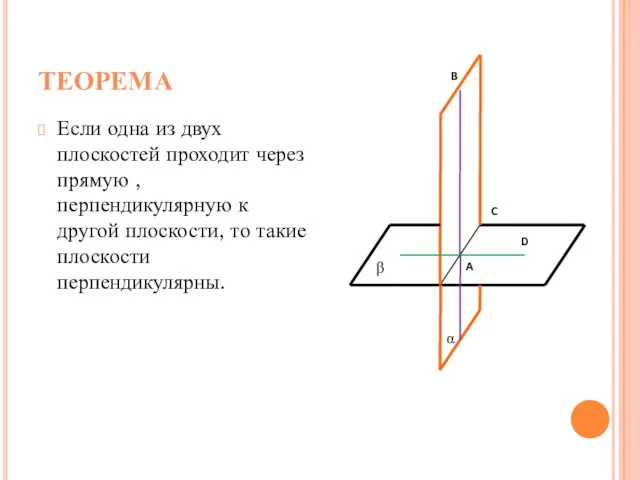
ТЕОРЕМА
Если одна из двух плоскостей проходит через прямую , перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

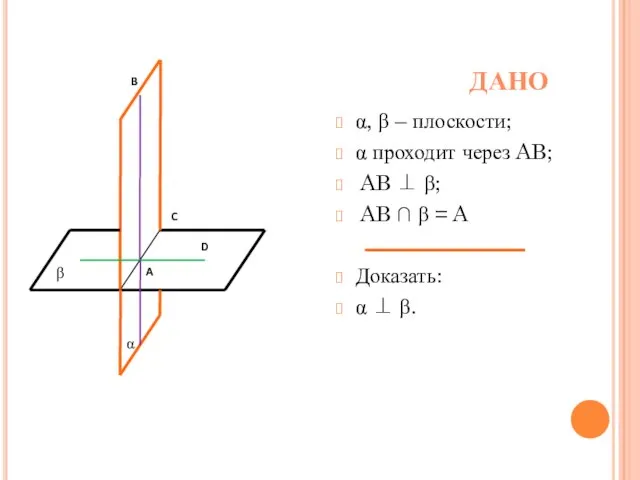
ДАНО
α, β – плоскости;
α проходит через AB;
AB ⊥ β;
AB ∩ β = A
Доказать:
α ⊥ β.

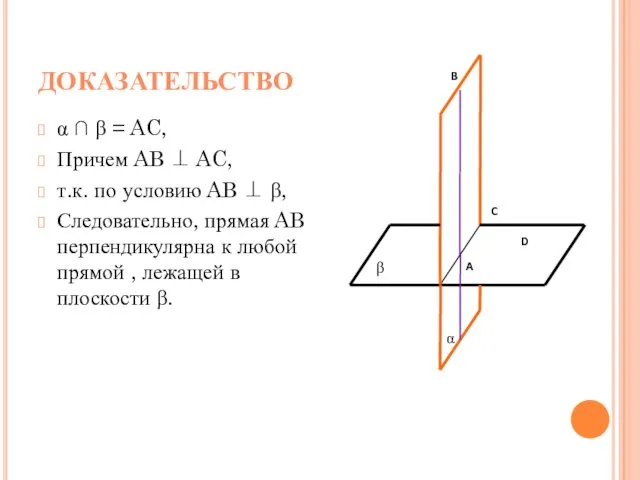
ДОКАЗАТЕЛЬСТВО
α ∩ β = AC,
Причем AB ⊥ AC,
т.к. по условию AB ⊥ β,
Следовательно, прямая AB перпендикулярна к любой прямой , лежащей в плоскости β.

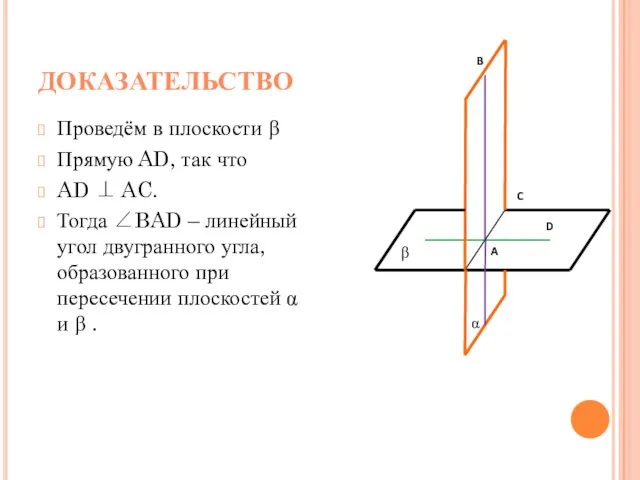
ДОКАЗАТЕЛЬСТВО
Проведём в плоскости β
Прямую AD, так что
AD ⊥ AC.
Тогда ∠BAD – линейный угол двугранного угла, образованного при пересечении плоскостей α и β .
A

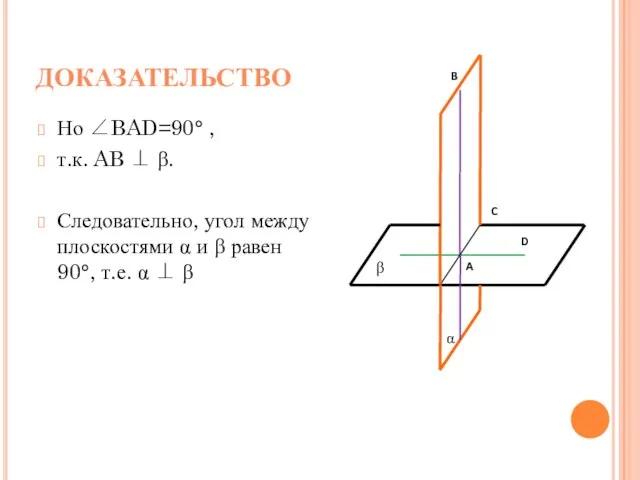
ДОКАЗАТЕЛЬСТВО
Но ∠BAD=90° ,
т.к. AB ⊥ β.
Следовательно, угол между плоскостями α и β равен 90°, т.е. α ⊥ β